Encryption and Decryption in Digital Communications

This chapter is from the book

Digital Communications: Fundamentals and Applications, 3rd Edition

Learn More Buy

This chapter is from the book

This chapter is from the book 

Digital Communications: Fundamentals and Applications, 3rd Edition

Learn More Buy

17.3 Practical Security

For ciphertext sequences greater than the unicity distance, any system can be solved, in principle, merely by trying each possible key until the unique solution is obtained. This is completely impractical, however, except when the key is extremely small. For example, for a key configured as a permutation of the alphabet, there are 26! ≈ 4 × 10²⁶ possibilities (considered small in the cryptographic context). In an exhaustive search, one might expect to reach the right key at about halfway through the search. If we assume that each trial requires a computation time of 1 s, the total search time exceeds 10¹² years. Hence techniques other than a brute-force search (e.g., statistical analysis) must be employed if a cryptanalyst is to have any hope of success.

17.3.1 Confusion and Diffusion

A statistical analysis using the frequency of occurrence of individual characters and character combinations can be used to solve many cipher systems. Shannon [5] suggested two encryption concepts for frustrating the statistical endeavors of the cryptanalyst. He termed these encryption transformations confusion and diffusion. Confusion involves substitutions that render the final relationship between the key and ciphertext as complex as possible. This makes it difficult to utilize a statistical analysis to narrow the search to a particular subset of the key variable space. Confusion ensures that the majority of the key is needed to decrypt even very short sequences of ciphertext. Diffusion involves transformations that smooth out the statistical differences between characters and between character combinations. An example of diffusion with a 26-letter alphabet is to transform a message sequence M = M₀, M₁, . . . into a new message sequence Y = Y₀, Y₁, . . . according to the relationship

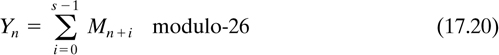
where each character in the sequence is regarded as an integer modulo-26, s is some chosen integer, and n = 0, 1, 2, .... The new message, Y, will have the same redundancy as the original message, M, but the letter frequencies of Y will be more uniform than in M. The effect is that the cryptanalyst needs to intercept a longer sequence of ciphertext before any statistical analysis can be useful.

17.3.2 Substitution

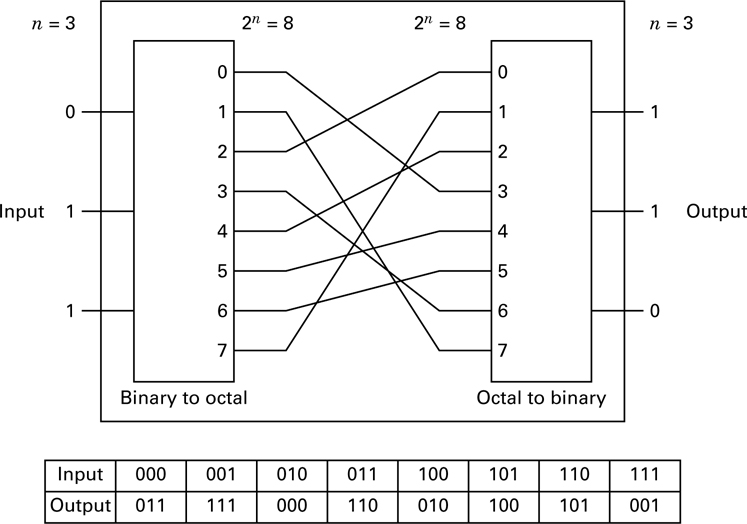
Substitution encryption techniques, such as the Caesar cipher and the Trithemius progressive key cipher, are widely used in puzzles. Such simple substitution ciphers offer little encryption protection. For a substitution technique to fulfill Shannon’s concept of confusion, a more complex relationship is required. Figure 17.6 shows one example of providing greater substitution complexity through the use of a nonlinear transformation. In general, n input bits are first represented as one of 2ⁿ different characters (binary-to-octal transformation in the example of Figure 17.6). The set of 2 characters is then permuted so that each character is transposed to one of the others in the set. The character is then converted back to an n-bit output.

Figure 17.6 Substitution box.

It can be easily shown that there are (2ⁿ)! different substitution or connection patterns possible. The cryptanalyst’s task becomes computationally unfeasible as n gets large, say n = 128; then 2ⁿ = 10³⁸, and (2ⁿ)! is an astronomical number. We recognize that for n = 128, this substitution box (S-box) transformation is complex (confusion). However, although we can identify the S-box with n = 128 as ideal, its implementation is not feasible because it would require a unit with 2ⁿ = 10³⁸ wiring connections.

To verify that the S-box example in Figure 17.6 performs a nonlinear transformation, we need only use the superposition theorem stated below as a test. Let

where a and b are input terms, C and C′ are output terms, and T is the transformation. Then

If T is linear: C = C′ for all inputs

If T is nonlinear: C ≠ C′

Suppose that a = 001 and b = 010; then, using T as described in Figure 17.6, we obtain

C = T (001) T (010) = 111 000 = 111

C′ = T (001 010) = T (011) = 110

where the symbol represents modulo-2 addition. Since C ≠ C′ , the S-box is nonlinear.

17.3.3 Permutation

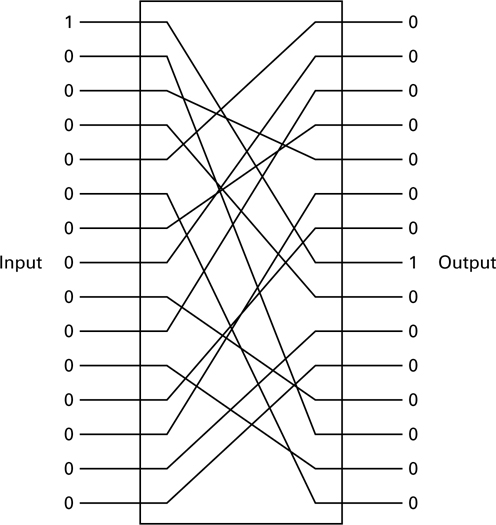
In permutation (transposition), the positions of the plaintext letters in the message are simply rearranged, rather than being substituted with other letters of the alphabet as in the classic ciphers. For example, the word THINK might appear, after permutation, as the ciphertext HKTNI. Figure 17.7 represents an example of binary data permutation (a linear operation). Here we see that the input data are simply rearranged or permuted (P-box). The technique has one major disadvantage when used alone; it is vulnerable to trick messages. A trick message is

Figure 17.7 Permutation box.

illustrated in Figure 17.7. A single 1 at the input and all the rest 0 quickly reveals one of the internal connections. If the cryptanalyst can subject the system to a plaintext attack, he will transmit a sequence of such trick messages, moving the single 1 one position for each transmission. In this way, each of the connections from input to output is revealed. This is an example of why a system’s security should not depend on its architecture.

17.3.4 Product Cipher System

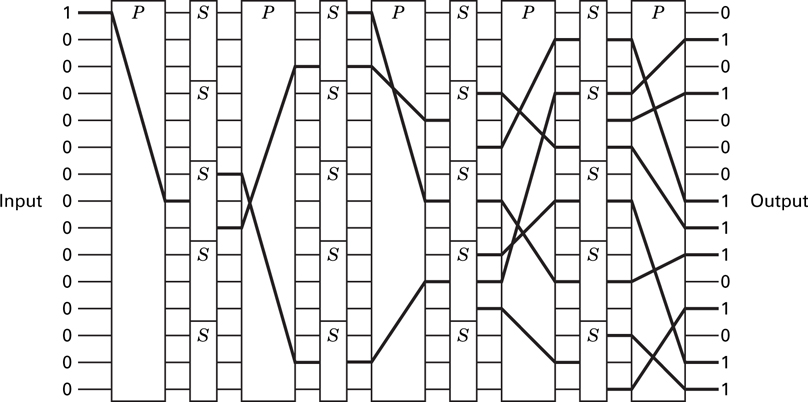
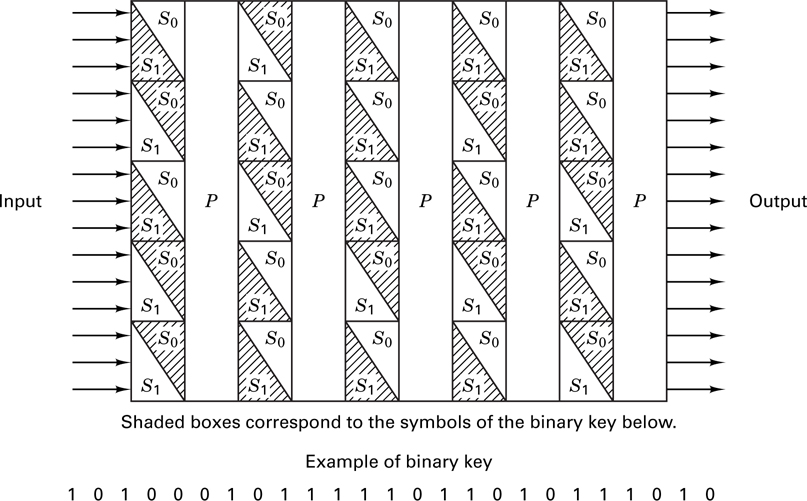
For transformation involving reasonable numbers of n-message symbols, both of the foregoing cipher systems (the S-box and the P-box) are by themselves wanting. Shannon [5] suggested using a product cipher or a combination of S-box and P-box transformations, which together could yield a cipher system more powerful than either one alone. This approach of alternately applying substitution and permutation transformations has been used by IBM in the LUCIFER system [7, 8] and has become the basis for the national Data Encryption Standard (DES) [9]. Figure 17.8 illustrates such a combination of P-boxes and S-boxes. Decryption is accomplished by running the data backward, using the inverse of each S-box. The system as pictured in Figure 17.8 is difficult to implement since each S-box is different, a randomly generated key is not usable, and the system does not lend itself to repeated use of the same circuitry. To avoid these difficulties, the LUCIFER system [8] used two different types of S-boxes, S₁ and S₀, which could be publicly revealed. Figure17.9 illustrates such a system. The input data are transformed by the sequence of S-boxes and P-boxes under the dictates of a key. The 25-bit key in this example designates, with a binary one or zero, the choice (S₁ or S₀) of each of the 25 S-boxes in the block. The details of the encryption devices can be revealed since security of the system is provided by the key.

Figure 17.8 Product cipher system.

The iterated structure of the product cipher system in Figure 17.9 is typical of most present-day block ciphers. The messages are partitioned into successive blocks of n bits, each of which is encrypted with the same key. The n-bit block represents one of 2ⁿ different characters, allowing for (2ⁿ)! different substitution patterns. Consequently, for a reasonable implementation, the substitution part of the encryption scheme is performed in parallel on small segments of the block. An example of this is seen in the next section.

Figure 17.9 Individual keying capability.

17.3.5 The Data Encryption Standard

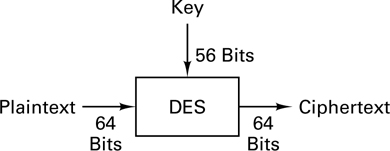
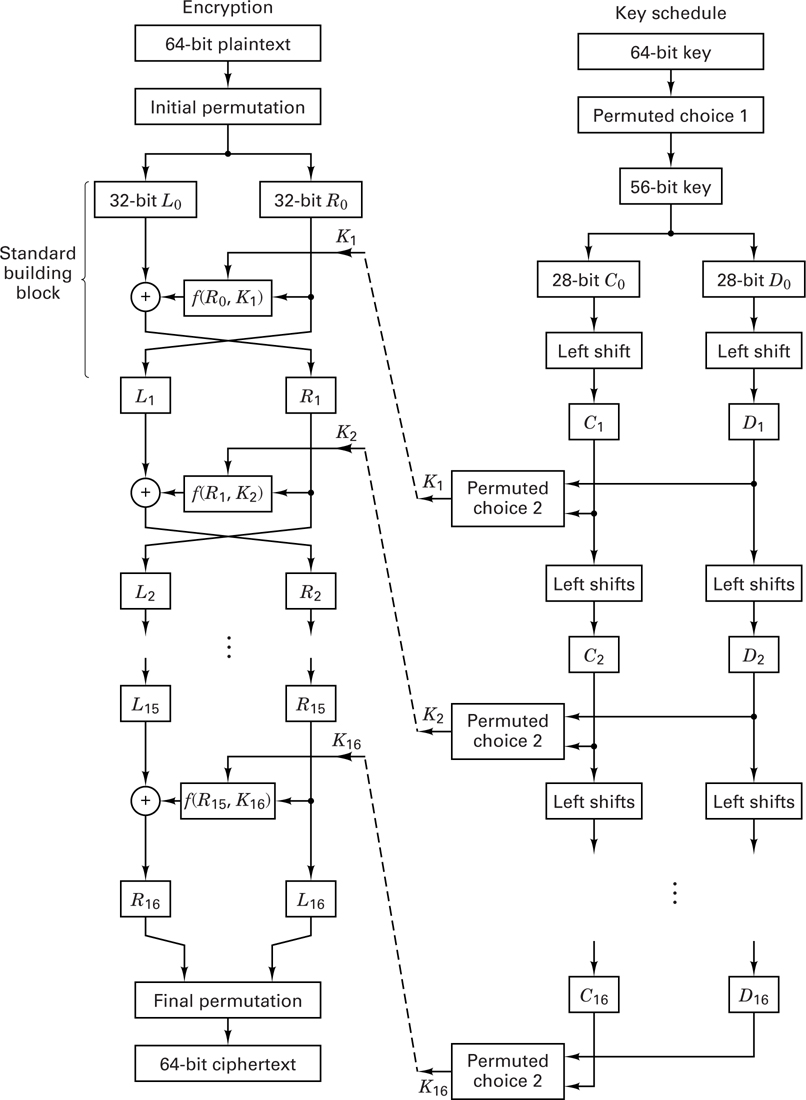
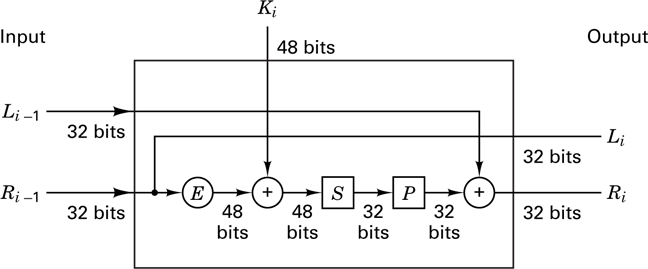
In 1977, the National Bureau of Standards adopted a modified Lucifer system as the national Data Encryption Standard (DES) [9]. From a system input-output point of view, DES can be regarded as a block encryption system with an alphabet size of 2 symbols, as shown in Figure 17.10. An input block of 64 bits, regarded as a plaintext symbol in this alphabet, is replaced with a new ciphertext symbol. Figure 17.11 illustrates the system functions in block diagram form. The encryption algorithm starts with an initial permutation (IP) of the 64 plaintext bits, described in the IP-table (Table 17.1). The IP-table is read from left to right and from top to bottom, so that bits x₁, x₂, . . . , x₆₄ are permuted to x₅₈, x₅₀, . . . , x₇. After this initial permutation, the heart of the encryption algorithm consists of 16 iterations using the standard building block (SBB) shown in Figure 17.12. The standard building block uses 48 bits of key to transform the 64 input data bits into 64 output data bits, designated as 32 left-half bits and 32 right-half bits. The output of each building block becomes the input to the next building block. The input right-half 32 bits (R_i-1) are copied unchanged to become the output left-half 32 bits (L_i). The R_{i- 1} bits are also extended and transformed into 48 bits with the E-table (Table 17.2), and then modulo-2 summed with the 48 bits of the key. As in the case of the IP-table, the E-table is read from left to right and from top to bottom. The table expands bits

Figure 17.10 Data encryption standard (DES) viewed as a block encryption system.

Figure 17.11 Data encryption standard.

Figure 17.12 Standard building block (SBB).

Table 17.1 Initial Permutation (IP)

Table 17.2 E-Table Bit Selection

R_i-1 = x₁, x₂, ... , x₃₂

into

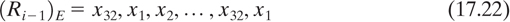
Notice that the bits listed in the first and last columns of the E-table are those bit positions that are used twice to provide the 32 bit-to-48 bit expansion.

Next, (R_i-1)_E is modulo-2 summed with the ith key selection, explained later, and the result is segmented into eight 6-bit blocks

B₁, B₂, ... , B₈

That is,

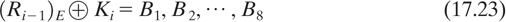
Each of the eight 6-bit blocks, B_j, is then used as an input to an S-box function which returns a 4-bit block, S_j(B_j). Thus the input 48 bits are transformed by the S-box to 32 bits. The S-box mapping function, S_j, is defined in Table 17.3. The transformation of B_j = b₁, b₂, b₃, b₄, b₅, b₆ is accomplished as follows. The integer corresponding to bits, b₁, b₆ selects a row in the table, and the integer corresponding to bits b₂ b₃ b₄ b₅ selects a column in the table. For example, if b₁ = 110001, then S₁ returns the value in row 3, column 8, which is the integer 5 and is represented by the bit sequence 0101. The resulting 32-bit block out of the S-box is then permuted using the P-table (Table 17.4). As in the case of the other tables, the P-table is read from left to right and from top to bottom, so that bits x₁, x₂, . . . , x₃₂ are permuted to x₁₆, x₇, . . . , x₂₅. The 32-bit output of the P-table is modulo-2 summed with the input left-half 32 bits (L_{i - 1}), forming the output right-half 32 bits (R_i).

Table 17.3 S-Box Selection Functions

Table 17.4 P-Table Permutation

The algorithm of the standard building block can be represented by

where f(R_{i – 1}, K_i) denotes the functional relationship comprising the E-table, S-box, and P-table we have described. After 16 iterations of the SBB, the data are transposed according to the final inverse permutation (IP^- 1) described in the IP^- 1-table (Table 17.5), where the output bits are read from left to right and from top to bottom, as before.

Table 17.5 Final Permutation (IP^- 1)

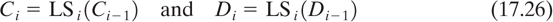
where LS_i is a left circular shift by the number of positions shown in Table 17.7. The sequence C_i, D_i is then transposed according to the permuted choice 2 (PC-2) shown in Table 17.8. The result is the key sequence K_i, which is used in the ith iteration of the encryption algorithm.

Table 17.7 Key Schedule of Left Shifts

Table 17.8 Key Permutation PC-2

The DES can be implemented as a block encryption system (see Figure17.11), which is sometimes referred to as a codebook method. A major disadvantage of this method is that a given block of input plaintext will always result in the same output ciphertext (under the same key). Another encryption mode, called the cipher feedback mode, encrypts single bits rather than characters, resulting in a stream encryption system [3]. With the cipher feedback scheme (described later), the encryption of a segment of plaintext not only depends on the key and the current data, but also on some of the earlier data.

Since the late 1970s, two points of contention have been widely publicized about the DES [10]. The first concerns the key variable length. Some researchers felt that 56 bits are not adequate to preclude an exhaustive search. The second concerns the details of the internal structure of the S-boxes, which were never released by IBM. The National Security Agency (NSA), which had been involved in the testing of the DES algorithm, had requested that the information not be publicly discussed, because it was sensitive. The critics feared that NSA had been involved in design selections that would allow NSA to “tap into” any DES-encrypted messages [10]. DES is no longer a viable choice for strong encryption. The 56-bit key can be found in a matter of days with relatively inexpensive computer tools [11]. (Some alternative algorithms are discussed in Section 17.6.)