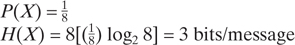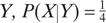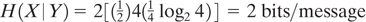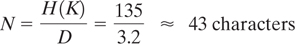This chapter is from the book
This chapter is from the book
This chapter is from the book
17.2 The Secrecy of a Cipher System
17.2.1 Perfect Secrecy
Consider a cipher system with a finite message space {M} = M0, M1, . . . , MN - 1 and a finite ciphertext space {C} = C0, C1,... , CU – 1. For any Mi, the a priori probability that Mi is transmitted is P(Mi). Given that Cj is received, the a posteriori probability that Mi was transmitted is P(Mi |Cj). A cipher system is said to have perfect secrecy if for every message Mi and every ciphertext Cj, the a posteriori probability is equal to the a priori probability:
Thus, for a system with perfect secrecy, a cryptanalyst who intercepts Cj obtains no further information to enable him or her to determine which message was transmitted. A necessary and sufficient condition for perfect secrecy is that for every Mi and Cj,
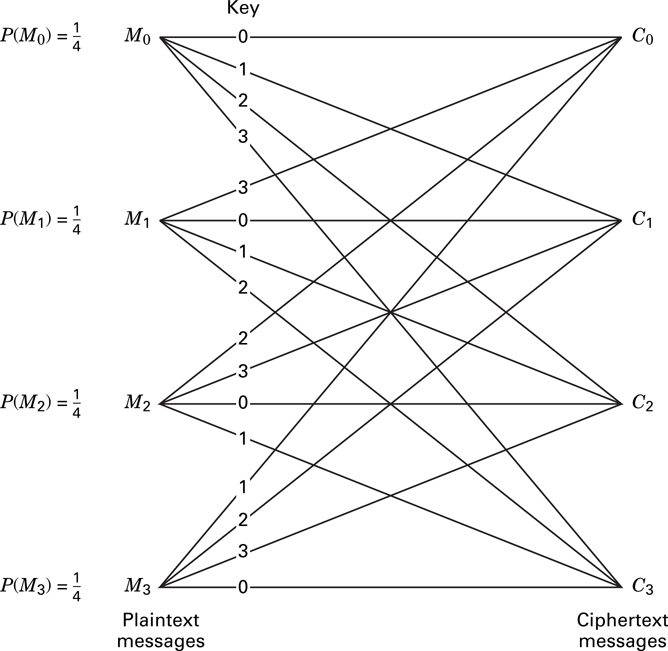
The schematic in Figure 17.4 illustrates an example of perfect secrecy. In this example, {M} = M0, M1, M2, M3, {C} = C0, C1, C2, C3, {K} = K0, K1, K2, K3, N = U = 4,
)
and P(Mi) = P(Cj) =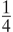 
. The transformation from message to ciphertext is obtained by
where TKj indicates a transformation under the key, Kj, and x modulo-y is defined as the remainder of dividing x by y. Thus s = 0, 1, 2, 3. A cryptanalyst intercepting one of the ciphertext messages Cs = C0, C1, C2, or C3 would have no way of determining which of the four keys was used, and therefore whether the correct message is M0, M1, M2, or M3. A cipher system in which the number of messages, the number of keys, and the number of ciphertext transformations are all equal is said to have perfect secrecy if and only if the following two conditions are met:
There is only one key transforming each message to each ciphertext.
All keys are equally likely.
If these conditions are not met, there would be some message Mi such that for a given Cj, there is no key that can decipher Cj into Mi, implying that P(Mi |Cj) = 0 for some i and j. The cryptanalyst could then eliminate certain plaintext messages from consideration, thereby simplifying the task. Perfect secrecy is a very desirable objective since it means that the cipher system is unconditionally secure. It should be apparent, however, that for systems which transmit a large number of messages, the amount of key that must be distributed for perfect secrecy can result in formidable management problems, making such systems impractical. Since in a system with perfect secrecy, the number of different keys is at least as great as the number of possible messages, if we allow messages of unlimited length, perfect secrecy requires an infinite amount of key.
)
){kind=link}
17.2.2 Entropy and Equivocation
As discussed in Chapter 9, the amount of information in a message is related to the probability of occurrence of the message. Messages with probability of either 0 or 1 contain no information, since we can be very confident concerning our prediction of their occurrence. The more uncertainty there is in predicting the occurrence of a message, the greater is the information content. Hence when each of the messages in a set is equally likely, we can have no confidence in our ability to predict the occurrence of a particular message, and the uncertainty or information content of the message is maximum.
Entropy, H(X), is defined as the average amount of information per message. It can be considered a measure of how much choice is involved in the selection of a message X. It is expressed by the following summation over all possible messages:
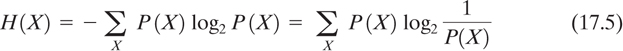
When the logarithm is taken to the base 2, as shown, H(X) is the expected number of bits in an optimally encoded message X. This is not quite the measure that a cryptanalyst desires. He will have intercepted some ciphertext and will want to know how confidently he can predict a message (or key) given that this particular ciphertext was sent. Equivocation, defined as the conditional entropy of X given Y, is a more useful measure for the cryptanalyst in attempting to break the cipher and is given by
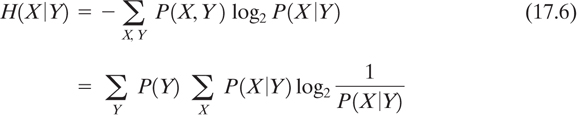
Equivocation can be thought of as the uncertainty that message X was sent, having received Y. The cryptanalyst would like H(X Y) to approach zero as the amount of intercepted ciphertext, Y, increases.
EXAMPLE 17.3 ENTROPY AND EQUIVOCATION
Consider a sample message set consisting of eight equally likely messages {X} = X1, X2,... , X8.
(a) Find the entropy associated with a message from the set {X}.
(b) Given another equally likely message set {Y} = Y1, Y2. Consider that the occur-rence of each message Y narrows the possible choices of X in the following way:
If Y1 is present: only X1, X2, X3, or X4 is possible
If Y2 is present: only X5, X6, X7, or X8 is possible
Find the equivocation of message X conditioned on message Y.
Solution
(a)
(b)
for four of the X’s and P(X|Y) = 0 for the remaining four X’s. Using Equation (17.6), we obtain
We see that knowledge of Y has reduced the uncertainty of X from 3 bits/message to 2 bits/message.
17.2.3 Rate of a Language and Redundancy
The true rate of a language is defined as the average number of information bits contained in each character and is expressed for messages of length N by
where H(X) is the message entropy, or the number of bits in the optimally encoded message. For large N, estimates of r for written English range between 1.0 and 1.5 bits/character [4]. The absolute rate or maximum entropy of a language is defined as the maximum number of information bits contained in each character assuming that all possible sequences of characters are equally likely. The absolute rate is given by
where L is the number of characters in the language. For the English alphabet r′ = log2 26 = 4.7 bits/character. The true rate of English is, of course, much less than its absolute rate since, like most languages, English is highly redundant and structured.
The redundancy of a language is defined in terms of its true rate and absolute rate as
For the English language with r′ = 4.7 bits/character and r = 1.5 bits/character, D = 3.2, and the ratio D/r′ = 0.68 is a measure of the redundancy in the language.
17.2.4 Unicity Distance and Ideal Secrecy
We stated earlier that perfect secrecy requires an infinite amount of key if we allow messages of unlimited length. With a finite key size, the equivocation of the key H(K|C) generally approaches zero, implying that the key can be uniquely determined and the cipher system can be broken. The unicity distance is defined as the smallest amount of ciphertext, N, such that the key equivocation H(K|C) is close to zero. Therefore, the unicity distance is the amount of ciphertext needed to uniquely determine the key and thus break the cipher system. Shannon [5] described an ideal secrecy system as one in which H(K|C) does not approach zero as the amount of ciphertext approaches infinity; that is, no matter how much ciphertext is intercepted, the key cannot be determined. The term “ideal secrecy” describes a system that does not achieve perfect secrecy but is nonetheless unbreakable (unconditionally secure) because it does not reveal enough information to determine the key.
Most cipher systems are too complex to determine the probabilities required to derive the unicity distance. However, it is sometimes possible to approximate unicity distance, as shown by Shannon [5] and Hellman [6]. Following Hellman, assume that each plaintext and ciphertext message comes from a finite alphabet of L symbols.
Thus there are 2r′ N possible messages of length, N, where r′ is the absolute rate of the language. We can consider the total message space partitioned into two classes, meaningful messages, M1, and meaningless messages M2. We then have
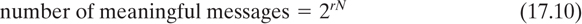
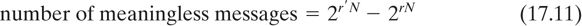
where r is the true rate of the language, and where the a priori probabilities of the message classes are
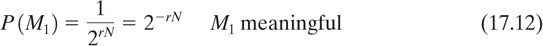
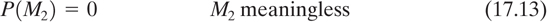
Let us assume that there are 2H(K) possible keys (size of the key alphabet), where H(K) is the entropy of the key (number of bits in the key). Assume that all keys are equally likely; that is,
The derivation of the unicity distance is based on a random cipher model, which states that for each key K and ciphertext C, the decryption operation DK(C) yields an independent random variable distributed over all the possible 2r′N messages (both meaningful and meaningless). Therefore, for a given K and C, the DK(C) operation can produce any one of the plaintext messages with equal probability.
Given an encryption described by Ci = EKi(Mi), a false solution F arises whenever encryption under another key Kj could also produce Ci either from the message Mi or from some other message Mj; that is,
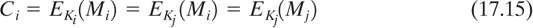
A cryptanalyst intercepting Ci would not be able to pick the correct key and hence could not break the cipher system. We are not concerned with the decryption operations that produce meaningless messages because these are easily rejected.
For every correct solution to a particular ciphertext there are 2H(K) - 1 incorrect keys, each of which has the same probability P(F) of yielding a false solution. Because each meaningful plaintext message is assumed equally likely, the probability of a false solution, is the same as the probability of getting a meaningful message, namely,
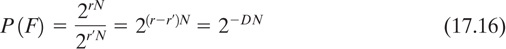
where D = r′ - r is the redundancy of the language. The expected number of false solutions 
is then
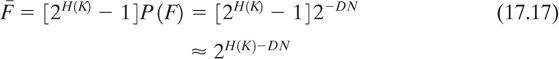
Because of the rapid decrease of with increasing N,
is defined as the point where the number of false solutions is sufficiently small so that the cipher can be broken. The resulting unicity distance is therefore
We can see from Equation (17.17) that if H(K) is much larger than DN, there will be a large number of meaningful decryptions, and thus a small likelihood of a cryptanalyst distinguishing which meaningful message is the correct message. In a loose sense, DN represents the number of equations available for solving for the key, and H(K) the number of unknowns. When the number of equations is smaller than the number of unknown key bits, a unique solution is not possible and the system is said to be unbreakable. When the number of equations is larger than the number of unknowns, a unique solution is possible and the system can no longer be characterized as unbreakable (although it may still be computationally secure).
It is the predominance of meaningless decryptions that enables cryptograms to be broken. Equation (17.19) indicates the value of using data compression techniques prior to encryption. Data compression removes redundancy, thereby increasing the unicity distance. Perfect data compression would result in D = 0 and N = ∞ for any key size.
EXAMPLE 17.4 UNICITY DISTANCE
Calculate the unicity distance for a written English encryption system, where the key is given by the sequence k1, k2, . . . , k29, where each ki is a random integer in the range (1, 25) dictating the shift number (Figure 17.3) for the ith character. Assume that each of the possible key sequences is equally likely.
Solution
There are (25)29 possible key sequences, each of which is equally likely. Therefore, using Equations (17.5), (17.8), and (17.19) we have
Key entropy: H (K) = log2 (25)29 = 135 bits
Absolute rate for English: r′ = log2 26 = 4.7 bits/character
Assumed true rate for English: r = 1.5 bits/character
Redundancy: D = r′ r = 3.2 bits/character
In Example 17.2, perfect secrecy was illustrated using the same type of key sequence described here, with a 29-character message. In this example we see that if the available ciphertext is 43 characters long (which implies that some portion of the key sequence must be used twice), a unique solution may be possible. However, there is no indication as to the computational difficulty in finding the solution. Even though we have estimated the theoretical amount of ciphertext required to break the cipher, it might be computationally infeasible to accomplish this.