This chapter is from the book
This chapter is from the book
This chapter is from the book
6.3 A2C Algorithm
Here we put the actor and critic together to form the Advantage Actor-Critic (A2C) algorithm, shown in Algorithm 6.1.
Algorithm 6.1 A2C algorithm
1: Set β ≥ 0 # entropy regularization weight
2: Set αA ≥ 0 # actor learning rate
3: Set αC ≥ 0 # critic learning rate
4: Randomly initialize the actor and critic parameters θA, θC4
5: for episode = 0 . . . MAX_EPISODE do
6: Gather and store data (st, at, rt, 
) by acting in the environment using
↪ the current policy
7: for t = 0 . . . T do
8: Calculate predicted V -value 
using the critic network θC
9: Calculate the advantage 
using the critic network θC
10: Calculate 
using the critic network θC and/or trajectory data
11: Optionally, calculate entropy Ht of the policy distribution, using
↪ the actor network θA. Otherwise, set β = 0
12: end for
13: Calculate value loss, for example using MSE:
14: 
15: Calculate policy loss:
16: 
17: Update critic parameters, for example using SGD:5
18: θC = θC + αC∇θCLval(θC)
19: Update actor parameters, for example using SGD:
20: θA = θA + αA∇θALpol(θA)
21: end for
Each algorithm we have studied so far focused on learning one of two things: how to act (a policy) or how to evaluate actions (a critic). Actor-Critic algorithms learn both together. Aside from that, each element of the training loop should look familiar, since they have been part of the algorithms presented earlier in this book. Let’s go through Algorithm 6.1 step by step.
Lines 1–3: Set the values of important hyperparameters: β, αA, αC. β determines how much entropy regularization to apply (see below for more details). αA and αC are the learning rates used when optimizing each of the networks. They can be the same or different. These values vary depending on the RL problem we are trying to solve, and need to be determined empirically.
Line 4: Randomly initialize the parameters of both networks.
Line 6: Gather some data using the current policy network θA. This algorithm shows episodic training, but this approach also applies to batch training.
Lines 8–10: For each (st, at, rt,
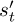) experience in the episode, calculate 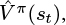, , 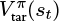and 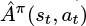using the critic network.Line 11: For each (st, at, rt,
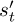) experience in the episode, optionally calculate the entropy of the current policy distribution πθA using the actor network. The role of entropy is discussed in detail in Box 6.2.Lines 13–14: Calculate the value loss. As with the DQN algorithms, we selected MSE6 as the measure of distance between
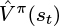and 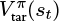. However, any other appropriate loss function, such as the Huber loss, could be used.
Lines 15–16: Calculate the policy loss. This has the same form as we saw in the REINFORCE algorithm with the addition of an optional entropy regularization term. Notice that we are minimizing the loss, but we want to maximize the policy gradient, hence the negative sign in front of
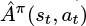log πθA(at | st) as in REINFORCE.Lines 17–18: Update the critic parameters using the gradient of the value loss.
Lines 19–20: Update the actor parameters using the policy gradient.
Box 6.2 Entropy Regularization
The role of entropy regularization is to encourage exploration through diverse actions. This idea was first proposed by Williams and Peng in 1991 [149] and has since become a popular modification to reinforcement learning algorithms which involve policy gradients.
To understand why it encourages exploration, first note that a distribution that is more uniform has higher entropy. The more uniform a policy’s action distribution is, the more diverse actions it produces. Conversely, policies which are less uniform and produce similar actions have low entropy.
Let’s see why the entropy modification to the policy gradient shown in Equation 6.21 encourages a more uniform policy.
)
Entropy H and β are always non-negative, so −βH is always negative. When a policy is far from uniform, entropy decreases, −βH increases and contributes more to the loss, and the policy will be encouraged to become more uniform. Conversely, when a policy is more uniform, entropy increases, −βH decreases and contributes less to the loss, and the policy will have little incentive to change through the entropy term.
Modifying the loss in this way expresses a preference for a greater variety of actions, provided that it does not reduce the term 
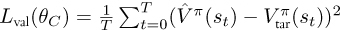
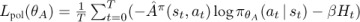
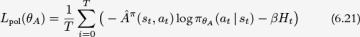
too much. The balance between these two terms of the objective is controlled through the β parameter.