- Cost Functions
- Optimization: Learning to Minimize Cost
- Backpropagation
- Tuning Hidden-Layer Count and Neuron Count
- An Intermediate Net in Keras
- Summary
- Key Concepts
This chapter is from the book
This chapter is from the book
This chapter is from the book
Optimization: Learning to Minimize Cost
Cost functions provide us with a quantification of how incorrect our model’s estimate of the ideal y is. This is most helpful because it arms us with a metric we can leverage to reduce our network’s incorrectness.
As alluded to a couple of times in this chapter, the primary approach for minimizing cost in deep learning paradigms is to pair an approach called gradient descent with another one called backpropagation. These approaches are optimizers and they enable the network to learn. This learning is accomplished by adjusting the model’s parameters so that its estimated ŷ gradually converges toward the target of y, and thus the cost decreases. We cover gradient descent first and move on to backpropagation immediately afterward.
Gradient Descent
Gradient descent is a handy, efficient tool for adjusting a model’s parameters with the aim of minimizing cost, particularly if you have a lot of training data available. It is widely used across the field of machine learning, not only in deep learning.
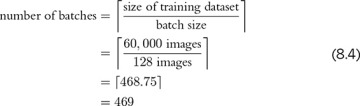
In Figure 8.2, we use a nimble trilobite in a cartoon to illustrate how gradient descent works. Along the horizontal axis in each frame is some parameter that we’ve denoted as p. In an artificial neural network, this parameter would be either a neuron’s weight w or bias b. In the top frame, the trilobite finds itself on a hill. Its goal is to descend the gradient, thereby finding the location with the minimum cost, C. But there’s a twist: The trilobite is blind! It cannot see whether deeper valleys lie far away somewhere, and so it can only use its cane to investigate the slope of the terrain in its immediate vicinity.
)
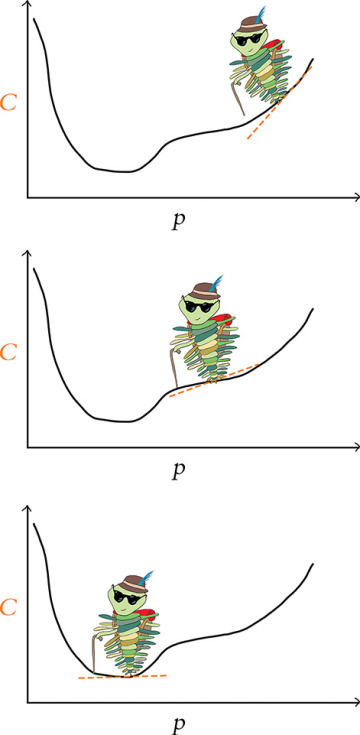
FIGURE 8.2 A trilobite using gradient descent to find the value of a parameter p associated with minimal cost, C
The dashed orange line in Figure 8.2 indicates the blind trilobite’s calculation of the slope at the point where it finds itself. According to that slope line, if the trilobite takes a step to the left (i.e., to a slightly lower value of p), it would be moving to a location with smaller cost. On the hand, if the trilobite takes a step to the right (a slightly higher value of p), it would be moving to a location with higher cost. Given the trilobite’s desire to descend the gradient, it chooses to take a step to the left.
By the middle frame, the trilobite has taken several steps to the left. Here again, we see it evaluating the slope with the orange line and discovering that, yet again, a step to the left will bring it to a location with lower cost, and so it takes another step left. In the lower frame, the trilobite has succeeded in making its way to the location—the value of the parameter p—corresponding to the minimum cost. From this position, if it were to take a step to the left or to the right, cost would go up, so it gleefully remains in place.
In practice, a deep learning model would not have only one parameter. It is not uncommon for deep learning networks to have millions of parameters, and some industrial applications have billions of them. Even our Shallow Net in Keras—one of the smallest models we build in this book—has 50,890 parameters (see Figure 7.5).
Although it’s impossible for the human mind to imagine a billion-dimensional space, the two-parameter cartoon shown in Figure 8.3 provides a sense of how gradient descent scales up to minimize cost across multiple parameters simultaneously. Across however many trainable parameters there are in a model, gradient descent iteratively evaluates slopes6 to identify the adjustments to those parameters that correspond to the steepest reduction in cost. With two parameters, as in the trilobite cartoon in Figure 8.3, for example, this procedure can be likened to a blind hike through the mountains, where:
Latitude represents one parameter, say p1.
Longitude represents the other parameter, p2.
Altitude represents cost—the lower the altitude, the better!
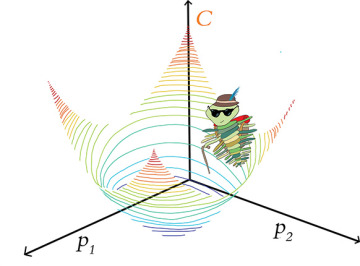
FIGURE 8.3 A trilobite exploring along two model parameters—p1 and p2—in order to minimize cost via gradient descent. In a mountain-adventure analogy, p1 and p2 could be thought of as latitude and longitude, and altitude represents cost.
)
The trilobite randomly finds itself at a location in the mountains. From that point, it feels around with its cane to identify the direction of the step it can take that will reduce its altitude the most. It then takes that single step. Repeating this process many times, the trilobite may eventually find itself at the latitude and longitude coordinates that correspond to the lowest-possible altitude (the minimum cost), at which point the trilobite’s surreal alpine adventure is complete.
Learning Rate
For conceptual simplicity, in Figure 8.4, let’s return to a blind trilobite navigating a single-parameter world instead of a two-parameter world. Now let’s imagine that we have a ray-gun that can shrink or enlarge trilobites. In the middle panel, we’ve used our ray-gun to make our trilobite very small. The trilobite’s steps will then be correspondingly small, and so it will take our intrepid little hiker a long time to find its way to the legendary valley of minimum cost. On the other hand, consider the bottom panel, in which we’ve used our ray-gun to make the trilobite very large. The situation here is even worse! The trilobite’s steps will now be so large that it will step right over the valley of minimum cost, and so it never has any hope of finding it.
)
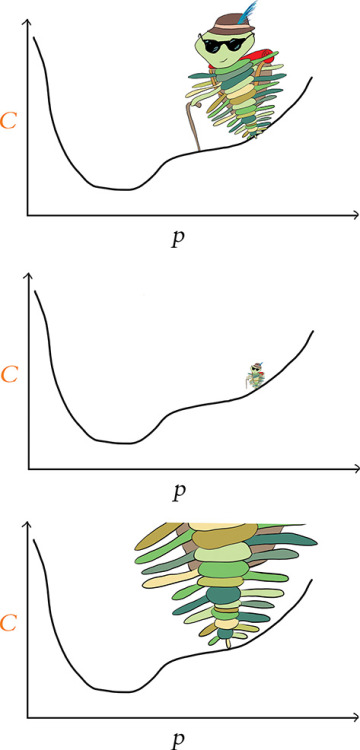
FIGURE 8.4 The learning rate (η) of gradient descent expressed as the size of a trilobite. The middle panel has a small learning rate, and the bottom panel, a large one.
In gradient descent terminology, step size is referred to as learning rate and denoted with the Greek letter η (eta, pronounced “ee-ta”). Learning rate is the first of several model hyperparameters that we cover in this book. In machine learning, including deep learning, hyperparameters are aspects of the model that we configure before we begin training the model. So hyperparameters such as η are preset while, in contrast, parameters—namely, w and b—are learned during training.
Getting your hyperparameters right for a given deep learning model often requires some trial and error. For the learning rate η, it’s something like the fairy tale of “Goldilocks and the Three Bears”: Too small and too large are both inadequate, but there’s a sweet spot in the middle. More specifically, as we portray in Figure 8.4, if η is too small, then it will take many, many iterations of gradient descent (read: an unnecessarily long time) to reach the minimal cost. On the other hand, selecting a value for η that is too large means we might never reach minimal cost at all: The gradient descent algorithm will act erratically as it jumps right over the parameters associated with minimal cost.
Coming up in Chapter 9, we have a clever trick waiting for you that will circumnavigate the need for you to manually select a given neural network’s η hyperparameter. In the interim, however, here are our rules of thumb on the topic:
Begin with a learning rate of about 0.01 or 0.001.
If your model is able to learn (i.e., if cost decreases consistently epoch over epoch) but training happens very slowly (i.e., each epoch, the cost decreases only a small amount), then increase your learning rate by an order of magnitude (e.g., from 0.01 to 0.1). If the cost begins to jump up and down erratically epoch over epoch, then you’ve gone too far, so rein in your learning rate.
At the other extreme, if your model is unable to learn, then your learning rate may be too high. Try decreasing it by orders of magnitude (e.g., from 0.001 to 0.0001) until cost decreases consistently epoch over epoch. For a visual, interactive way to get a handle on the erratic behavior of a model when its learning rate is too high, you can return to the TensorFlow Playground example from Figure 1.18 and dial up the value within the “Learning rate” dropdown box.
Batch Size and Stochastic Gradient Descent
When we introduced gradient descent, we suggested that it is efficient for machine learning problems that involve a large dataset. In the strictest sense, we outright lied to you. The truth is that if we have a very large quantity of training data, ordinary gradient descent would not work at all because it wouldn’t be possible to fit all of the data into the memory (RAM) of our machine.
Memory isn’t the only potential snag; compute power could cause us headaches, too. A relatively large dataset might squeeze into the memory of our machine, but if we tried to train a neural network containing millions of parameters with all those data, vanilla gradient descent would be highly inefficient because of the computational complexity of the associated high-volume, high-dimensional calculations.
Thankfully, there’s a solution to these memory and compute limitations: the stochastic variant of gradient descent. With this variation, we split our training data into mini-batches—small subsets of our full training dataset—to render gradient descent both manageable and productive.
Although we didn’t focus on it at the time, when we trained the model in our Shallow Net in Keras notebook back in Chapter 5 we were already using stochastic gradient descent by setting our optimizer to SGD in the model.compile() step. Further, in the subsequent line of code when we called the model.fit() method, we set batch_size to 128 to specify the size of our mini-batches—the number of training data points that we use for a given iteration of SGD. Like the learning rate η presented earlier in this chapter, batch size is also a model hyperparameter.
Let’s work through some numbers to make the concepts of batches and stochastic gradient descent more tangible. In the MNIST dataset, there are 60,000 training images.
With a batch size of 128 images, we then have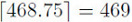 
batches7,8 of gradient descent per epoch:
)
Before carrying out any training, we initialize our network with random values for each neuron’s parameters w and b.9 To begin the first epoch of training:
We shuffle and divide the training images into mini-batches of 128 images each. These 128 MNIST images provide 784 pixels each, which all together constitute the inputs x that are passed into our neural network. It’s this shuffling step that puts the stochastic (which means random) in “stochastic gradient descent.”
By forward propagation, information about the 128 images is processed by the network, layer through layer, until the output layer ultimately produces ŷ values.
A cost function (e.g., cross-entropy cost) evaluates the network’s ŷ values against the true y values, providing a cost C for this particular mini-batch of 128 images.
To minimize cost and thereby improve the network’s estimates of y given x, the gradient descent part of stochastic gradient descent is performed: Every single w and b parameter in the network is adjusted proportional to how much each contributed to the error (i.e., the cost) in this batch (note that the adjustments are scaled by the learning rate hyperparameter η ).10
These four steps constitute a round of training, as summarized by Figure 8.5.
)
FIGURE 8.5 An individual round of training with stochastic gradient descent. Although mini-batch size is a hyperparameter that can vary, in this particular case, the mini-batch consists of 128 MNIST digits, as exemplified by our hike-loving trilobite carrying a small bag of data.
Figure 8.6 captures how rounds of training are repeated until we run out of training images to sample. The sampling in step 1 is done without replacement, meaning that at the end of an epoch each image has been seen by the algorithm only once, and yet between different epochs the mini-batches are sampled randomly. After a total of 468 rounds, the final batch contains only 96 samples.
)
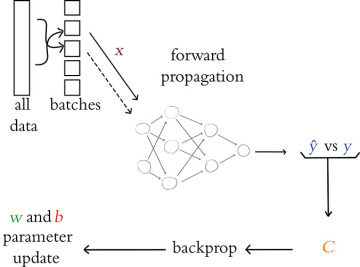
FIGURE 8.6 An outline of the overall process for training a neural network with stochastic gradient descent. The entire dataset is shuffled and split into batches. Each batch is forward propagated through the network; the output ŷ is compared to the ground truth y and the cost C is calculated; backpropagation calculates the gradients; and the model parameters w and b are updated. The next batch (indicated by a dashed line) is forward propagated, and so on until all of the batches have moved through the network. Once all the batches have been used, a single epoch is complete and the process starts again with a reshuffling of the full training dataset.
This marks the end of the first epoch of training. Assuming we’ve set our model up to train for further epochs, we begin the next epoch by replenishing our pool with all 60,000 training images. As we did through the previous epoch, we then proceed through a further 469 rounds of stochastic gradient descent.11 Training continues in this way until the total desired number of epochs is reached.
The total number of epochs that we set our network to train for is yet another hyperparameter, by the way. This hyperparameter, though, is one of the easiest to get right:
If the cost on your validation data is going down epoch over epoch, and if your final epoch attained the lowest cost yet, then you can try training for additional epochs.
Once the cost on your validation data begins to creep upward, that’s an indicator that your model has begun to overfit to your training data because you’ve trained for too many epochs. (We elaborate much more on overfitting in Chapter 9.)
There are methods12 you can use to automatically monitor training and validation cost and stop training early if things start to go awry. In this way, you could set the number of epochs to be arbitrarily large and know that training will continue until the validation cost stops improving—and certainly before the model begins overfitting!
Escaping the Local Minimum
In all of the examples of gradient descent thus far in the chapter, our hiking trilobite has encountered no hurdles on its journey toward minimum cost. There are no guarantees that this would be the case, however. Indeed, such smooth sailing is unusual.
Figure 8.7 shows the mountaineering trilobite exploring the cost of some new model that is being used to solve some new problem. With this new problem, the relationship between the parameter p and cost C is more complex. To have our neural network estimate y as accurately as possible, gradient descent needs to identify the parameter values associated with the lowest-attainable cost. However, as our trilobite makes its way from its random starting point in the top panel, gradient descent leads it to getting trapped in a local minimum. As shown in the middle panel, while our intrepid explorer is in the local minimum, a step to the left or a step to the right both lead to an increase in cost, and so the blind trilobite stays put, completely oblivious of the existence of a deeper valley—the global minimum—lying yonder.
All is not lost, friends, for stochastic gradient descent comes to the rescue here again. The sampling of mini-batches can have the effect of smoothing out the cost curve, as exemplified by the dashed curve shown in the bottom panel of Figure 8.7. This smoothing happens because the estimate is noisier when estimating the gradient from a smaller mini-batch (versus from the entire dataset). Although the actual gradient in the local minimum truly is zero, estimates of the gradient from small subsets of the data don’t provide the complete picture and might give an inaccurate reading, causing our trilobite to take a step left thinking there is a gradient when there really isn’t one. This noisiness and inaccuracy is paradoxically a good thing! The incorrect gradient may result in a step that is large enough for the trilobite to escape the local valley and continue making its way down the mountain. Thus, by estimating the gradient many times on these mini-batches, the noise is smoothed out and we are able to avoid local minima. In summary, although each mini-batch on its own lacks complete information about the cost curve, in the long run—over a large number of mini-batches—this tends to work to our advantage.
)
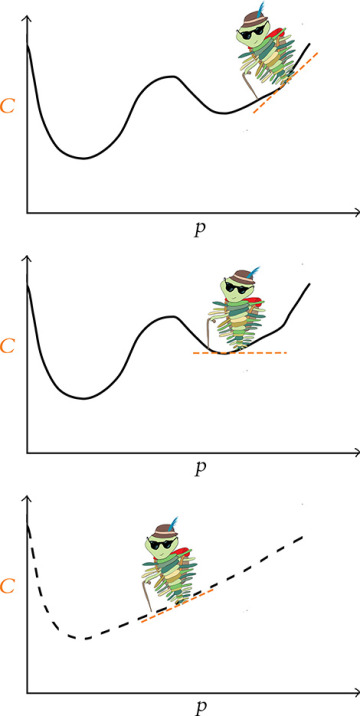
FIGURE 8.7 A trilobite applying vanilla gradient descent from a random starting point (top panel) is ensnared by a local minimum of cost (middle panel). By turning to stochastic gradient descent in the bottom panel, the daring trilobite is able to bypass the local minimum and make its way toward the global minimum.
Like the learning rate hyperparameter η, there is also a Goldilocks-style sweet spot for batch size. If the batch size is too large, the estimate of the gradient of the cost function is far more accurate. In this way, the trilobite has a more exacting impression of the gradient in its immediate vicinity and is able to take a step (proportional to η) in the direction of the steepest possible descent. However, the model is at risk of becoming trapped in local minima as described in the preceding paragraph.13 Besides that, the model might not fit in memory on your machine, and the compute time per iteration of gradient descent could be very long.
On the other hand, if the batch size is too small, each gradient estimate may be excessively noisy (because a very small subset of the data is being used to estimate the gradient of the entire dataset) and the corresponding path down the mountain will be unnecessarily circuitous; training will take longer because of these erratic gradient descent steps. Furthermore, you’re not taking advantage of the memory and compute resources on your machine.14 With that in mind, here are our rules of thumb for finding the batch-size sweet spot:
Start with a batch size of 32.
If the mini-batch is too large to fit into memory on your machine, try decreasing your batch size by powers of 2 (e.g., from 32 to 16).
If your model trains well (i.e., cost is going down consistently) but each epoch is taking very long and you are aware that you have RAM to spare,15 you could experiment with increasing your batch size. To avoid getting trapped in local minima, we don’t recommend going beyond 128.