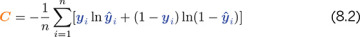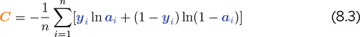Training Deep Networks
Become acquainted with two techniques—called gradient descent and backpropagation—that work in tandem to learn artificial neural network parameters.
Save 35% off the list price* of the related book or multi-format eBook (EPUB + MOBI + PDF) with discount code ARTICLE.
* See informit.com/terms
In the preceding chapters, we described artificial neurons comprehensively and we walked through the process of forward propagating information through a network of neurons to output a prediction, such as whether a given fast food item is a hot dog, a juicy burger, or a greasy slice of pizza. In those culinary examples from Chapters 6 and 7, we fabricated numbers for the neuron parameters—the neuron weights and biases. In real-world applications, however, these parameters are not typically concocted arbitrarily: They are learned by training the network on data.
In this chapter, you will become acquainted with two techniques—called gradient descent and backpropagation—that work in tandem to learn artificial neural network parameters. As usual in this book, our presentation of these methods is not only theoretical: We provide pragmatic best practices for implementing the techniques. The chapter culminates in the application of these practices to the construction of a neural network with more than one hidden layer.
Cost Functions
In Chapter 7, you discovered that, upon forward propagating some input values all the way through an artificial neural network, the network provides its estimated output, which is denoted ŷ. If a network were perfectly calibrated, it would output ŷ values that are exactly equal to the true label y. In our binary classifier for detecting hot dogs, for example (Figure 7.3), y = 1 indicated that the object presented to the network is a hot dog, while y = 0 indicated that it’s something else. In an instance where we have in fact presented a hot dog to the network, therefore, ideally it would output ŷ = 1.
In practice, the gold standard of ŷ = y is not always attained and so may be an excessively stringent definition of the “correct” ŷ. Instead, if y = 1 we might be quite pleased to see a ŷ of, say, 0.9997, because that would indicate that the network has an extremely high confidence that the object is a hot dog. A ŷ of 0.9 might be considered acceptable, ŷ = 0.6 to be disappointing, and ŷ = 0.1192 (as computed in Equation 7.7) to be awful.
To quantify the spectrum of output-evaluation sentiments from “quite pleased” all the way down to “awful,” machine learning algorithms often involve cost functions (also known as loss functions). The two such functions that we cover in this book are called quadratic cost and cross-entropy cost. Let’s cover them in turn.
Quadratic Cost
Quadratic cost is one of the simplest cost functions to calculate. It is alternatively called mean squared error, which handily describes all that there is to its calculation:
For any given instance i, we calculate the difference (the error) between the true label yi and the network’s estimated ŷi. We then square this difference, for two reasons:
Squaring ensures that whether y is greater than ŷ or vice versa, the difference between the two is stated as a positive value.
Squaring penalizes large differences between y and ŷ much more severely than small differences.
Having obtained a squared error for each instance i by using (yi − ŷi)2, we can then calculate the mean cost C across all n of our instances by:
Summing up cost across all instances using
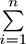
Dividing by however many instances we have using
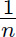
By taking a peek inside the Quadratic Cost Jupyter notebook from the book’s GitHub repo, you can play around with Equation 8.1 yourself. At the top of the notebook, we define a function to calculate the squared error for an instance i:
def squared_error(y, yhat):
return (y - yhat)**2
By plugging a true y of 1 and the ideal yhat of 1 in to the function by using squared_error(1, 1), we observe that—as desired—this perfect estimate is associated with a cost of 0. Likewise, minor deviations from the ideal, such as a yhat of 0.9997, correspond to an extremely small cost: 9.0e-08.1 As the difference between y and yhat increases, we witness the expected exponential increase in cost: Holding y steady at 1 but lowering yhat from 0.9 to 0.6, and then to 0.1192, the cost climbs increasingly rapidly from 0.01 to 0.16 and then to 0.78. As a final bit of amusement in the notebook, we note that had y truly been 0, our yhat of 0.1192 would be associated with a small cost: 0.0142.
Saturated Neurons
While quadratic cost serves as a straightforward introduction to loss functions, it has a vital flaw. Consider Figure 8.1, in which we recapitulate the tanh activation function from Figure 6.10. The issue presented in the figure, called neuron saturation, is common across all activation functions, but we’ll use tanh as our lone exemplar. A neuron is considered saturated when the combination of its inputs and parameters (interacting as per “the most important equation,” z = w · x + b, which is captured in Figure 6.10) produces extreme values of z—the areas encircled with red in the plot in Figure 8.1. In these areas, changes in z (via adjustments to the neuron’s underlying parameters w and b) cause only teensy-weensy changes in the neuron’s activation a.2
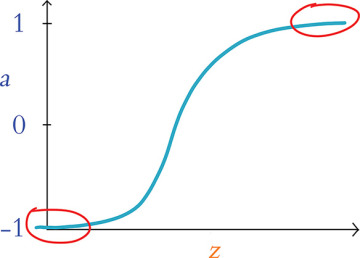
FIGURE 8.1 Plot reproducing the tanh activation function shown in Figure 6.10, drawing attention to the high and low values of z at which a neuron is saturated
Using methods that we cover later in this chapter—namely, gradient descent and backpropagation—a neural network is able to learn to approximate y through the tuning of the parameters w and b associated with all of its constituent neurons. In a saturated neuron, where changes to w and b lead to only minuscule changes in a, this learning slows to a crawl: If adjustments to w and b make no discernible impact on a given neuron’s activation a, then these adjustments cannot have any discernible impact downstream (via forward propagation) on the network’s ŷ, its estimate of y.
Cross-Entropy Cost
One of the ways3 to minimize the impact of saturated neurons on learning speed is to use cross-entropy cost in lieu of quadratic cost. This alternative loss function is configured to enable efficient learning anywhere within the activation function curve of Figure 8.1. Because of this, it is a far more popular choice of cost function and it is the selection that predominates the remainder of this book.4
You need not preoccupy yourself with the equation for cross-entropy cost, but for the sake of completeness, here it is:
The most pertinent aspects of the equation are:
Like quadratic cost, divergence of ŷ from y corresponds to increased cost.
Analogous to the use of the square in quadratic cost, the use of the natural logarithm ln in cross-entropy cost causes larger differences between ŷ and y to be associated with exponentially larger cost.
Cross-entropy cost is structured so that the larger the difference between ŷ and y, the faster the neuron is able to learn.5

To make it easier to remember that the greater the cost, the more quickly a neural network incorporating cross-entropy cost learns, here’s an analogy that would absolutely never involve any of your esteemed authors: Let’s say you’re at a cocktail party leading the conversation of a group of people that you’ve met that evening. The strong martini you’re holding has already gone to your head, and you go out on a limb by throwing a risqué line into your otherwise charming repartee. Your audience reacts with immediate, visible disgust. With this response clearly indicating that your quip was well off the mark, you learn pretty darn quickly. It’s exceedingly unlikely you’ll be repeating the joke anytime soon.
Anyway, that’s plenty enough on disasters of social etiquette. The final item to note on cross-entropy cost is that, by including ŷ, the formula provided in Equation 8.2 applies to only the output layer. Recall from Chapter 7 (specifically the discussion of Figure 7.3) that ŷ is a special case of a: It’s actually just another plain old a value—except that it’s being calculated by neurons in the output layer of a neural network. With this in mind, Equation 8.2 could be expressed with ai substituted in for ŷi so that the equation generalizes neatly beyond the output layer to neurons in any layer of a network:
To cement all of this theoretical chatter about cross-entropy cost, let’s interactively explore our aptly named Cross Entropy Cost Jupyter notebook. There is only one dependency in the notebook: the log function from the NumPy package, which enables us to compute the natural logarithm ln shown twice in Equation 8.3. We load this dependency using from numpy import log.
Next, we define a function for calculating cross-entropy cost for an instance i:
def cross_entropy(y, a):
return -1*(y*log(a) + (1-y)*log (1-a))
Plugging the same values in to our cross_entropy() function as we did the squared_ error() function earlier in this chapter, we observe comparable behavior. As shown in Table 8.1, by holding y steady at 1 and gradually decreasing a from the nearly ideal estimate of 0.9997 downward, we get exponential increases in cross-entropy cost. The table further illustrates that—again, consistent with the behavior of its quadratic cousin—cross-entropy cost would be low, with an a of 0.1192, if y happened to in fact be 0. These results reiterate for us that the chief distinction between the quadratic and cross-entropy functions is not the particular cost value that they calculate per se, but rather it is the rate at which they learn within a neural net—especially if saturated neurons are involved.
Table 8.1 Cross-entropy costs associated with selected example inputs
y |
a |
C |
|---|---|---|
1 |
0.9997 |
0.0003 |
1 |
0.9 |
0.1 |
1 |
0.6 |
0.5 |
1 |
0.1192 |
2.1 |
0 |
0.1192 |
0.1269 |
1 |
1− 0.1192 |
0.1269 |