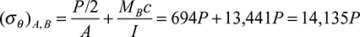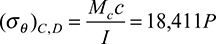- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
5.16 Combined Tangential and Normal Stresses
Curved beams are often loaded so that there is both an axial force and a moment on the cross section. The tangential stress given by Eq. (5.70) may then be algebraically added to the stress due to an axial force P acting through the centroid of cross-sectional area A. For this simple case of superposition, the total stress at a point located at distance r from the center of curvature O may be expressed as follows:
As before, a negative sign would be associated with a compressive load P.
Of course, the theory developed in this section applies only to the elastic stress distribution in curved beams. Stresses in straight members under various combined loads are discussed in detail throughout this text.
The following problems illustrate the application of the formulas developed to statically determinate and statically indeterminate beams under combined loadings. In the latter case, the energy method (Section 10.4) facilitates the determination of the unknown, redundant moment in the member.

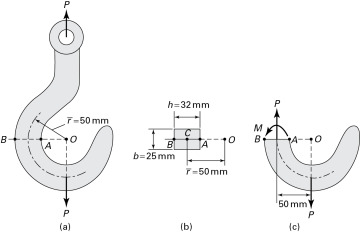
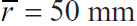 , b = 25 mm, and h = 32 mm.
, b = 25 mm, and h = 32 mm.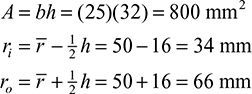
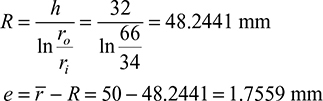
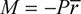 at the centroid of the section (
at the centroid of the section (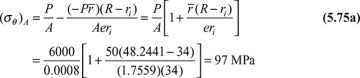
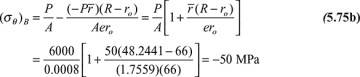
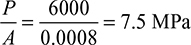
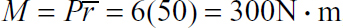 , gives
, gives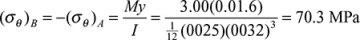
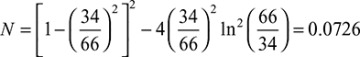
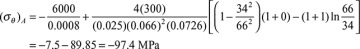
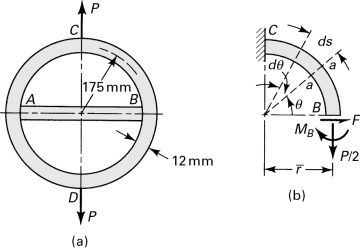
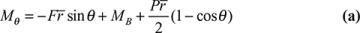
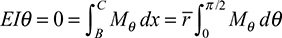
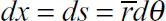 is the length of beam segment corresponding to dθ. Substituting in Eq. (a), this becomes, after integrating,
is the length of beam segment corresponding to dθ. Substituting in Eq. (a), this becomes, after integrating,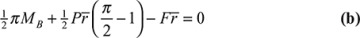
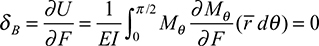
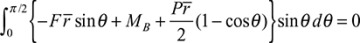
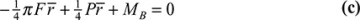
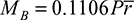
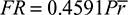 . Substituting Eq. (a) gives
. Substituting Eq. (a) gives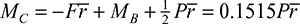
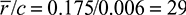 , the simple flexure formula offers the most efficient means of computation. The maximum stress is found at points A and B:
, the simple flexure formula offers the most efficient means of computation. The maximum stress is found at points A and B: