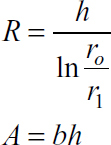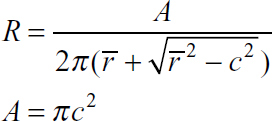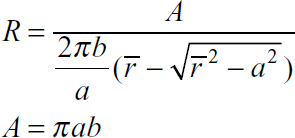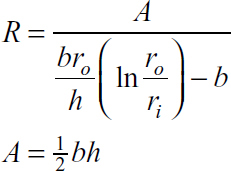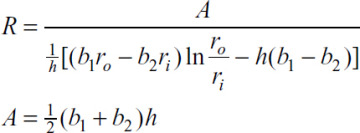- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.14 Curved Beam Formula
The approach to curved beams explored in this section was developed by E. Winkler (1835—1888). As an extension of the elementary theory of straight beams, Winkler′s theory assumes that all conditions required to make the straight-beam formula applicable are satisfied except that the beam is initially curved.
Consider the pure bending of a curved beam as illustrated in Fig. 5.25a. The distance from the center of curvature to the centroidal axis is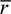 
. The positive y coordinate is measured toward the center of curvature O from the neutral axis (Fig. 5.25b). The outer and inner fibers are at distances of ro and ri from the center of curvature, respectively.
)
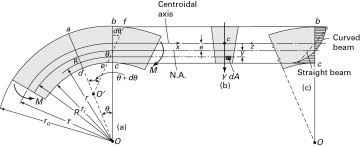
Figure 5.25. (a) Curved beam in pure bending with a cross-sectional vertical (y) axis of symmetry; (b) cross section; (c) stress distributions over the cross section.
5.14.1 Basic Assumptions
Derivation of the stress in the beam is again based on the three principles of solid mechanics and the familiar presuppositions:
All cross sections possess a vertical axis of symmetry lying in the plane of the centroidal axis passing through C.
The beam is subjected to end couples M. The bending moment vector is everywhere normal to the plane of symmetry of the beam.
Sections originally plane and perpendicular to the centroidal beam axis remain so subsequent to bending. (The influence of transverse shear on beam deformation is not taken into account.)
Referring to assumption (3), note the relationship in Fig. 5.25a between lines bc and ef representing the plane sections before and after the bending of an initially curved beam. Note also that the initial length of a beam fiber such as gh depends on the distance r from the center of curvature O. On the basis of plane sections remaining plane, we can state that the total deformation of a beam fiber obeys a linear law, as the beam element rotates through small angle.
5.14.2 Location of the Neutral Axis
In Fig. 5.25a, it is clear that the initial length of any arbitrary fiber gh of the beam depends on the distance r from the center of curvature O. Thus, the total deformation of a beam fiber obeys a linear law, as the beam element rotates through a small angle dθ. Conversely, the normal or tangential strain ɛθ does not follow a linear relationship. The contraction of fiber gh equals -(R - r)dθ where R is the distance from O to the neutral axis (yet to be determined) and its initial length is rθ. So, the normal strain of this fiber is given by ɛθ = - (R - r)dθ/rθ. For convenience, we denote λ = dθ/θ which is constant for any element.
The tangential normal stress, acting on an area dA of the cross section, can now be obtained through the use of Hooke8217;s law, σθ = Eɛθ. It follows that
)
The equations of equilibrium, ΣFx = 0 and ΣMz = 0 are, respectively,
)
)
When the tangential stress of Eq. (a) is inserted into Eq. (b), we obtain
)
Since Eλ and R are constants, they may be moved outside the integral sign, as follows:
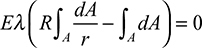
The radius of the neutral axis R is then written in the form
)
where A is the cross-sectional area of the beam. The integral in Eq. (5.68) may be evaluated for various cross-sectional shapes (see Example 5.13 and Probs. 5.46 through 5.48). For reference, Table 5.3 lists explicit formulas for R and A for some commonly used cases.
Table 5.3. Properties for Various Cross-Sectional Shapes
Cross Section |
Radius of Neutral Surface R |
|---|---|
A. Rectangle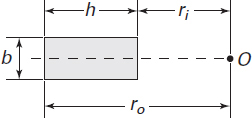 
|
|
B. Circle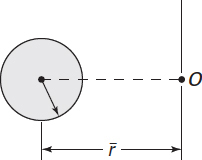 
|
|
C. Ellipse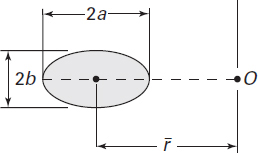 
|
|
D. Triangle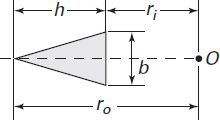 
|
|
E. Trapezoid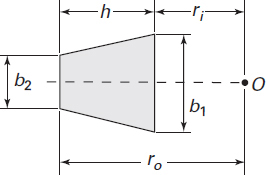 
|
|
)
The distance e between the centroidal axis and the neutral axis (y = 0) of the cross section of a curved beam (Fig. 5.25b) is equal to
)
Thus, in a curved member, the neutral axis does not coincide with the centroidal axis. This differs from the case involving straight elastic beams.
5.14.3 Tangential Stress
Once we know the location of the neutral axis, we can obtain the equation for the stress distribution by introducing Eq. (a) into Eq. (c). Therefore,
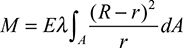
Expanding this equation, we have
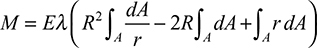
Here, the first integral is equivalent to A/R, as determined by Eq. (5.68), and the second integral equals the cross-sectional area A. The third integral, by definition, represents 
, where 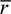is the radius of the centroidal axis. Therefore, 
.
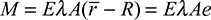We now introduce E from Eq. (a) into the discussion and solve for σθ from the resulting expression. Then, the tangential stress in a curved beam, subject to pure bending at a distance r from the center of curvature, is expressed in the following form:
)
where e is defined by Eq. (5.69). Alternatively, substituting y = R − r or r = R − y (Fig. 5.25a) into Eq. (5.70) yields
)
5.14.4 Winkler’s Formula
Equations (5.70) and (5.71) represent two forms of the curved-beam formula. Another alternative form of these equations is often referred to as Winkler’s formula. The variation of stress over the cross section is hyperbolic, as sketched in Fig. 5.25c. The sign convention applied to bending moment is the same as that used in Section 5.13—namely, the bending moment is positive when directed toward the concave side of the beam, as shown in the figure. If Eq. (5.70) or Eq. (5.71) results in a positive value, a tensile stress is present.