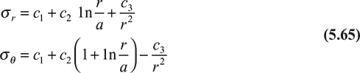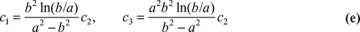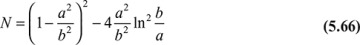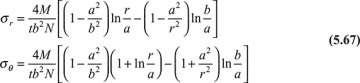- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.13 Elasticity Theory
Our treatment of stresses and deflections caused by the bending has been restricted so far to straight members. In real-world applications, many members—such as crane hooks, chain links, C-lamps, and punch-press frames—are curved and loaded as beams. Part C deals with the stresses caused by the bending of bars that are initially curved.
A curved bar or beam is a structural element for which the locus of the centroids of the cross sections is a curved line. This section focuses on an application of the theory of elasticity to a bar characterized by a constant narrow rectangular cross section and a circular axis. The axis of symmetry of the cross section lies in a single plane throughout the length of the member.
5.13.1 Equations of Equilibrium and Compatibility
Consider a beam subjected to equal end couples M such that bending takes place in the plane of curvature, as shown in Fig. 5.24a. Given that the bending moment remains constant along the length of the bar, the stress distribution should be identical in any radial cross section. Stated differently, we seek a distribution of stress displaying θ independence. It is clear that the appropriate expression of equilibrium is Eq. (8.2):
)
and that the condition of compatibility for plane stress, Eq. (3.41),
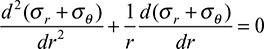
must also be satisfied. The latter is an equidimensional equation, which can be reduced to a second-order equation with constant coefficients by substituting r = et or t = In r. Direct integration then leads to σr +, σθ = c" + c′ 1n r which may be written in the form σr + σθ = c′'' + c′ In (r/a). Solving this expression together with Eq. (a) results in the following equations for the radial and tangential stress:
)
)
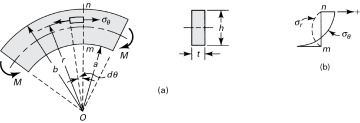
Figure 5.24. Pure bending of a curved beam of rectangular cross section.
5.13.2 Boundary Conditions
To evaluate the constants of integration, the boundary conditions are applied as follows:
No normal forces act along the curved boundaries at r = a and r = b, so that
Because there is no force acting at the ends, the normal stresses acting at the straight edges of the bar must be distributed to yield a zero resultant:
where t represents the beam thickness.
The normal stresses at the ends must produce a couple M:
)
)
)
The conditions (c) and (d) apply not just at the ends; that is, because of σθ independence, they apply at any θ. In addition, shearing stresses are assumed to be zero throughout the beam, so τrθ = 0 is satisfied at the boundaries, where no tangential forces exist.
Combining the first equation of Eqs. (5.65) with the condition (b), we find that
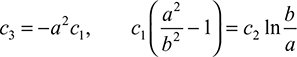
These constants together with the second of Eqs. (5.65) satisfy condition (c). Thus, we have
)
Finally, substitution of the second of Eqs. (5.65) and (e) into (d) provides
)
where
)
5.13.3 Stress Distribution
When the expressions for constants c1, c2 and c3 are inserted into Eq. (5.65), the following equations are obtained for the radial stress and tangential stress:
)
If the end moments are applied so that the force couples producing them are distributed in the manner indicated by Eq. (5.67), then these equations are applicable throughout the bar. If the distribution of applied stress (to produce M) differs from Eq. (5.67), the results may be regarded as valid in regions away from the ends, in accordance with Saint-Venant′s principle.
These results, when applied to a beam with radius a, large relative to its depth h, yield an interesting comparison between straight and curved beam theory. For slender beams with h << a, the radial stress σr in Eq. (5.67) becomes negligible, and the tangential stress σθ is approximately the same as that obtained from My/I. Note that the radial stresses developed in nonslender curved beams made of isotropic materials are small enough that they can be neglected in analysis and design.
The bending moment is taken as positive when it tends to decrease the radius of curvature of the beam, as in Fig. 5.24a. Employing this sign convention, σr as determined from Eq. (5.67) is always negative, indicating that this stress is compressive. Similarly, when σθ is positive, the stress is tensile; otherwise, it is compressive. Figure 5.24b plots the stresses at section mn. Note that the maximum stress magnitude is found at the extreme fiber of the concave side.
5.13.4 Deflections
Substitution of σr and σθ from Eq. (5.67) into Hooke′s law provides expressions for the strains ɛθ, ɛr, and γrθ. The displacements u and υ then follow, upon integration, from the strain-displacement relationships, described by Eqs. (3.33). The resulting displacements indicate that plane sections of the curved beam subjected to pure bending remain plane subsequent to bending. Castigliano′s theorem (Section 5.12) is a particularly attractive method for determining the deflection of curved members.
For beams in which the depth of the member is small relative to the radius of curvature or, as is usually assumed,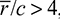 
, the initial curvature may be neglected in evaluating the strain energy. In such a case, 
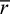represents the radius to the centroid, and c is the distance from the centroid to the extreme fiber on the concave side. Thus, the strain energy due to the bending of a straight beam [Eq. (5.62)] is also a good approximation for curved, slender beams.