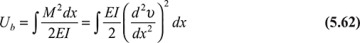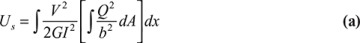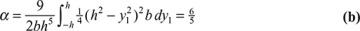- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.12 Energy Method for Deflections
Strain energy methods are frequently employed to analyze the deflections of beams and other structural elements. Of the many approaches available, Castigliano′s second theorem is one of the most widely used. To apply this theory, the strain energy must be represented as a function of loading. Detailed discussions of energy techniques are found in Chapter 10. In this section, we limit ourselves to a simple example to illustrate how the strain energy in a beam is evaluated and how the deflection is obtained by the use of Castigliano′s theorem (Section 10.4).
The strain energy stored in a beam under bending stress σx only, substituting M = EI(d2υ/dx2 into Eq. (2.63), is expressed in the form
)
where the integrations are carried out over the beam length. We next determine the strain energy stored in a beam that is only due to the shear loading V. As described in Section 5.7, this force produces shear stress τxy at every point in the beam. The strain energy density is, from Eq. (2.50), Uo = τxy/2G. Substituting τxy as expressed by Eq. (5.39), we have Uo = V2Q2/2GI2b2. Integrating this expression over the volume of the beam of cross-sectional area A, we obtain
)
5.12.1 Form Factor for Shear
Let us denote
)
This value is termed the shape or form factor for shear. When it is substituted in Eq. (a), we obtain
)
where the integration is carried over the beam length. The form factor is a dimensionless quantity specific to a given cross-section geometry.
For example, for a rectangular cross section of width b and height 2h, the first moment Q, from Eq. (5.41), is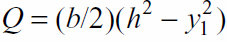 
. Because A/I2 = 9/2bh5, Eq. (5.63) provides the following result:
)
In a like manner, the form factor for other cross sections can be determined. Table 5.2 lists several typical cases. Following the determination of α the strain energy is evaluated by applying Eq. (5.64).
Table 5.2. Form Factor for Shear for Various Beam Cross Sections
Cross Section |
Form Factor α |
|---|---|
A. Rectangle |
6/5 |
B. I-section, box section, or channelsa |
A/Aweb |
C. Circle |
10/9 |
D. Thin-walled circular |
2 |
aA = area of the entire section, Aweb = area of the web ht, where h is the beam depth and t is the web thickness.
For a linearly elastic beam, Castigliano′s theorem, from Eq. (10.3), is expressed by
)
where P is a load acting on the beam and δ is the displacement of the point of application in the direction of P. Note that the strain energy U = Ub + Us is expressed as a function of the externally applied forces (or moments).
As an illustration, consider the bending of a cantilever beam of rectangular cross section and length L, subjected to a concentrated force P at the free end (Fig. 5.5). The bending moment at any section is M = Px and the shear force V is equal in magnitude to P. Substituting these together with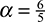 
into Eqs. (5.62) and (5.64) and integrating, we find the strain energy stored in the cantilever to be
){kind=link}
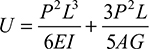
The displacement of the free end owing to bending and shear is, by application of Castigliano′s theorem, therefore
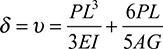
The exact solution is given by Eq. (5.24).
Part C: Curved Beams