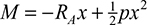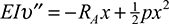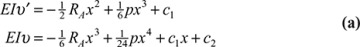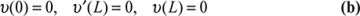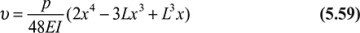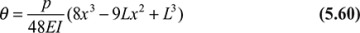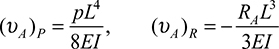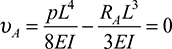- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
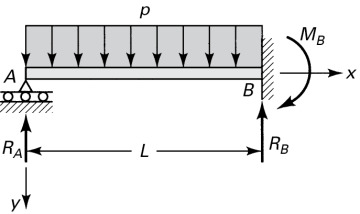
5.11 Statically Indeterminate Systems
A large class of problems of considerable practical interest relate to structural systems for which the equations of statics are not sufficient (but are necessary) for determination of the reactions or other unknown forces. Such systems are called statically indeterminate, and they require supplementary information for their solution. Additional equations usually describe certain geometric conditions associated with displacement or strain. These equations of compatibility state that the strain owing to deflection or rotation must preserve continuity.
With this additional information, the solution proceeds in essentially the same manner as for statically determinate systems. The number of reactions in excess of the number of equilibrium equations is called the degree of statical indeterminacy. Any reaction in excess of that which can be obtained by statics alone is said to be redundant. Thus, the number of redundants is the same as the degree of indeterminacy.
Several methods are available to analyze statically indeterminate structures. The principle of superposition, briefly discussed next, is an effective approach for many cases. In Section 5.6 and in Chapters 7 and 10, a number of commonly employed methods are discussed for the solution of the indeterminate beam, frame, and truss problems.
5.11.1 The Method of Superposition
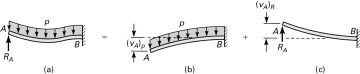
In the event of complicated load configurations, the method of superposition may be used to good advantage to simplify the analysis. Consider, for example, the continuous beam shown in Fig. 5.21a, which is then replaced by the beams shown in Fig. 5.21b and c. At point A, the beam now experiences the deflections (υA)p and (υA)R due to P and R, respectively. Subject to the restrictions imposed by small deformation theory and a material obeying Hooke′s law, the deflections and stresses are linear functions of transverse loadings, and superposition is valid:
)
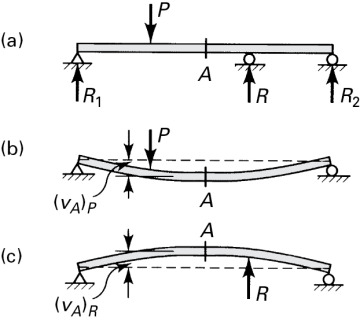
Figure 5.21. Superposition of displacements in a continuous beam.
This procedure may, in principle, be extended to situations involving any degree of indeterminacy.
EXAMPLE 5.11 DISPLACEMENTS OF A PROPPED CANTILEVER BEAM
Figure 5.22 shows a propped cantilever beam AB subject to a uniform load of intensity p. Determine (a) the reactions, (b) the equation of the deflection curve, and (c) the slope at A.
)
Figure 5.22. Example 5.11. A propped beam under uniform load.
Solution Reactions RA, RB and MB are statically indeterminate because there are only two equilibrium conditions (ΣFy = 0,Σ Mz = 0; thus, the beamis statically indeterminate to the first degree. With the origin of coordinates taken at the left support, the equation for the beam moment is
The third of Eqs. (5.32) then becomes
and successive integrations yield
)
There are three unknown quantities in these equations (c1,c2, and RA) and three boundary conditions:
)
Introducing Eqs. (b) into the preceding expressions, we obtain c2=0,c1=pL3/48 and
We can now determine the remaining reactions from the equations of equilibrium:
By substituting for RA, c1 and c2 in Eq. (a), we obtain the equation of the deflection curve:
Differentiating Eq. (5.59) with respect to x, we obtain the equation of the angle of rotation:
)
)
)
)
Setting x = 0 we have the slope at A:
)
EXAMPLE 5.12 REACTIONS OF A PROPPED CANTILEVER BEAM
Consider again the statically indeterminate beam shown in Fig. 5.22. Determine the reactions using the method of superposition.
Solution Reaction RA is selected as redundant; it becomes an unknown load when we eliminate the support at A (Fig. 5.23a). The loading is resolved into those shown in Figs. 5.23b and 5.23c. The solution for each case is (see Table D.4)
)
Figure 5.23. Example 5.12. Method of superposition: (a) reaction RA is selected as redundant; (b) deflection at end A due to load P; (c) deflection at end A due to reaction RA.
The compatibility condition for the original beam requires that
from which RA = 3pL/8. Reaction RB and moment MB can now be found from the equilibrium requirements. The results correspond to those of Example 5.11.