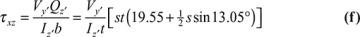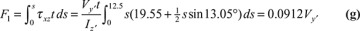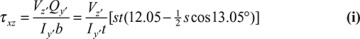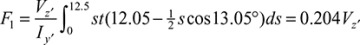- 5.1 Introduction
- 5.2 Pure Bending of Beams of Symmetrical Cross Section
- 5.3 Pure Bending of Beams of Asymmetrical Cross Section
- 5.4 Bending of A Cantilever of Narrow Section
- 5.5 Bending of a Simply Supported Narrow Beam
- 5.6 Elementary Theory of Bending
- 5.7 Normal and Shear Stresses
- 5.8 Effect of Transverse Normal Stress
- 5.9 Composite Beams
- 5.10 Shear Center
- 5.11 Statically Indeterminate Systems
- 5.12 Energy Method for Deflections
- 5.13 Elasticity Theory
- 5.14 Curved Beam Formula
- 5.15 Comparison of the Results of Various Theories
- 5.16 Combined Tangential and Normal Stresses
- References
- Problems
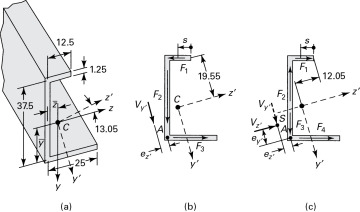
5.10 Shear Center
Given any cross-sectional configuration, one point may be found in the plane of the cross section through which the resultant of the transverse shearing stresses passes. A transverse load applied on the beam must act through this point, called the shear center or flexural center, if no twisting is to occur [Ref. 5.3]. The center of shear is sometimes defined as the point in the end section of a cantilever beam at which an applied load results in bending only. When the load does not act through the shear center, in addition to bending, a twisting action results (Section 6.1).
The location of the shear center is independent of the direction and magnitude of the transverse forces. For singly symmetrical sections, the shear center lies on the axis of symmetry, while for a beam with two axes of symmetry, the shear center coincides with their point of intersection (also the centroid). It is not necessary, in general, for the shear center to lie on a principal axis, and it may be located outside the cross section of the beam.
5.10.1 Thin-Walled Open Cross Sections
For thin-walled sections, the shearing stresses are taken to be distributed uniformly over the thickness of the wall and directed so as to parallel the boundary of the cross section. If the shear center S for the typical section of Fig. 5.18a is required, we begin by calculating the shear stresses by means of Eq. (5.39). The moment Mx of these stresses about arbitrary point A is then obtained. Since the external moment attributable to Vy about A is Vye, the distance between A and the shear center is given by
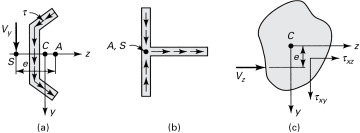
Figure 5.18. Shear centers.
If the force is parallel to the z axis rather than the y axis, the position of the line of action may be established in the manner discussed previously. If both Vy and Vz exist, the shear center is located at the intersection of the two lines of action.
The determination of Mx is simplified by propitious selection of point A, such as in Fig. 5.18b. There, the moment Mx of the shear forces about A is zero; point A is also the shear center. For all sections consisting of two intersecting rectangular elements, the same situation exists.
For thin-walled box beams (with boxlike cross section), the point or points in the wall where the shear flow q = 0 (or τxy = 0) is unknown. Here, shear flow is represented by the superposition of transverse and torsional flow (see Section 6.8). Hence, the unit angle of twist equation, Eq. (6.23), along with q = VQ/I, is required to find the shear flow for a cross section of a box beam. The analysis procedure is as follows: First, introduce a free edge by cutting the section open; second, close it again by obtaining the shear flow that makes the angle of twist in the beam zero [Refs. 5.4 through 5.6].
In the following examples, the shear center of an open, thin-walled section is determined for two typical situations. In the first, the section has only one axis of symmetry; in the second, there is an asymmetrical section.
5.10.2 Arbitrary Solid Cross Sections
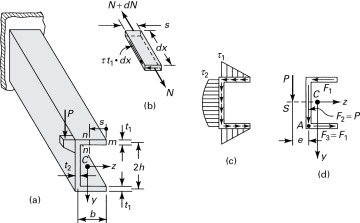
The preceding considerations can be extended to beams of arbitrary solid cross section, in which the shearing stress varies with both cross-sectional coordinates y and z. For these sections, the exact theory can, in some cases, be successfully applied to locate the shear center. Examine the section of Fig. 5.18c subjected to the shear force Vz, which produces the stresses indicated. Denote y and z as the principal directions. The moment about the x axis is then
Vz must be located a distance e from the z axis, where e = Mx/vz.





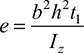
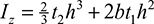

 and
and  with respect to nonprincipal axes z and y. By performing the procedure given in Example 5.1, we obtain
with respect to nonprincipal axes z and y. By performing the procedure given in Example 5.1, we obtain 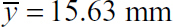
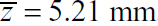 , Iy = 4765.62 mm4, Iz = 21,054.69 mm4, and Iyz = 3984.37 mm4. Equation (5.18) then yields the direction of the principal axis x′, y′ as θp = 13.05°, and Eq. (5.19) gives the principal moments of inertia as Iy′ = 3828.12 mm4, Iz′ = 21,953.12 mm4 (
, Iy = 4765.62 mm4, Iz = 21,054.69 mm4, and Iyz = 3984.37 mm4. Equation (5.18) then yields the direction of the principal axis x′, y′ as θp = 13.05°, and Eq. (5.19) gives the principal moments of inertia as Iy′ = 3828.12 mm4, Iz′ = 21,953.12 mm4 (