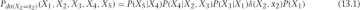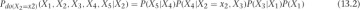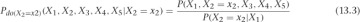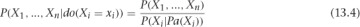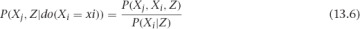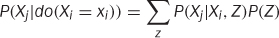- 13.1 Introduction
- 13.2 Experiments
- 13.3 Observation: An Example
- 13.4 Controlling to Block Non-causal Paths
- 13.5 Machine-Learning Estimators
- 13.6 Conclusion
This chapter is from the book
This chapter is from the book
This chapter is from the book
13.4 Controlling to Block Non-causal Paths
You just saw that you can take a correlative result and make it a causal result by controlling for the right variables. How do you know what variables to control for? How do you know that regression analysis will control for them? This section relies heavily on d-separation from Chapter 11. If that material isn’t fresh, you might want to review it now.
You saw in the previous chapter that conditioning can break statistical dependence. If you condition on the middle variable of a path X → Y → Z, you’ll break the dependence between X and Z that the path produces. If you condition on a confounding variable X ← Z → Y, you can break the dependence between X and Y induced by the confounder as well. It’s important to note that statistical dependence induced by other paths between X and Y is left unharmed by this conditioning. If, for example, you condition on Z in the system in Figure 13.10, you’ll get rid of the confounding but leave the causal dependence.
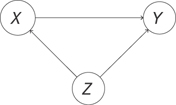
Figure 13.10 Conditioning on Z disrupts the confounding but leaves the causal statistical dependence between X and Y intact
If you had a general rule to choose which paths to block, you could eliminate all noncausal dependence between variables but save the causal dependence. The “back-door” criterion is the rule you’re looking for. It tells you what set of variables, Z, you should control for to eliminate any noncausal statistical dependence between Xi and Xj. You should note a final nuance before introducing the criterion. If you want to know if the correlation between Xi and Xj is “causal,” you have to worry about the direction of the effect. It’s great to know, for example, that the correlation “being on vacation” and “being relaxed” is not confounded, but you’d really like to know whether “being on vacation” causes you to “be relaxed.” That will inform a policy of going on vacation in order to be relaxed. If the causation were reversed, you couldn’t take that policy.
With that in mind, the back-door criterion is defined relative to an ordered pair of variables, (Xi, Xj), where Xi will be the cause, and Xj will be the effect.
We won’t prove this theorem, but let’s build some intuition for it. First, let’s examine the condition “no variable in Z is a descendant of Xi.” You learned earlier that if you condition on a common effect of Xi and Xj, then the two variables will be conditionally dependent, even if they’re normally independent. This remains true if you condition on any effect of the common effect (and so on down the paths). Thus, you can see that the first part of the back-door criterion prevents you from introducing extra dependence where there is none.
There is something more to this condition, too. If you have a chain like Xi → Xk → Xj, you see that Xk is a descendant of Xi. It’s not allowed in Z. This is because if you condition on Xk, you’d block a causal path between Xi and Xj. Thus, you see that the first condition also prevents you from conditioning on variables that fall along causal paths.
The second condition says “Z blocks every path between Xi and Xj that contains an arrow into Xi.” This part will tell us to control for confounders. How can you see this? Let’s consider some cases where there is one or more node along the path between Xi and Xj and the path contains an arrow into Xi. If there is a collider along the path between Xi and Xj, then the path is already blocked, so you just condition on the empty set to block that path. Next, if there is a fork along the path, like the path Xi ← Xk → Xj, and no colliders, then you have typical confounding. You can condition on any node along the path that will block it. In this case, you add Xk to the set Z. Note that there can be no causal path from Xi to Xj with an arrow pointing into Xi because of the arrow pointing into Xi.
Thus, you can see that you’re blocking all noncausal paths from Xi to Xj, and the remaining statistical dependence will be showing the causal dependence of Xj on Xi. Is there a way you can use this dependence to estimate the effects of interventions?
13.4.1 The G-formula
Let’s look at what it really means to make an intervention. What it means is that you have a graph like in Figure 13.11.
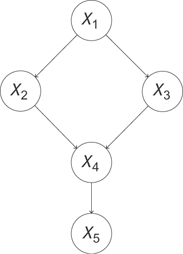
Figure 13.11 A pre-intervention causal graph. Data collected from this system reflects the way the world works when we just observe it.
You want to estimate the effect of X2 on X5. That is, you want to say “If I intervene in this system to set the value of X2 to x2, what will happen to X5? To quantify the effect, you have to realize that all of these variables are taking on values that depend not only on their predecessors but also on noise in the system. Thus, even if there’s a deterministic effect of X2 on X5 (say, raising the value of X5 by exactly one unit), you can only really describe the value X5 will take with a distribution of values. Thus, when you’re estimating the effect of X2 on X5, what you really want is the distribution of X5 when you intervene to set the value of X2.
Let’s look at what we mean by intervene. We’re saying we want to ignore the usual effect of X1 on X2 and set the value of X2 to x2 by applying some external force (our action) to X2. This removes the usual dependence between X2 and X1 and disrupts the downstream effect of X1 on X4 by breaking the path that passes through X2. Thus, we’ll also expect the marginal distribution between X1 and X4, P(X1, X4) to change, as well as the distribution of X1 and X5! Our intervention can affect every variable downstream from it in ways that don’t just depend on the value x2. We actually disrupt other dependences.
You can draw a new graph that represents this intervention. At this point, you’re seeing that the operation is very different from observing the value of X2 = x2, i.e., simply conditioning on X2 = x2. This is because you’re disrupting other dependences in the graph. You’re actually talking about a new system described by the graph in Figure 13.12.
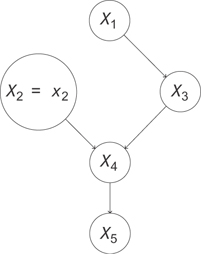
Figure 13.12 The graph representing the intervention do(x2 = x2). The statistics of this data will be different from that in from the system in Figure 13.11
You need some new notation to talk about an intervention like this, so you’ll denote do(X2 = x2) the intervention where you perform this operation. This gives you the definition of the intervention, or do-operation.
What does the joint distribution look like for this new graph? Let’s use the usual factorization, and write the following:
)
Here we’ve just indicated P(X2) by the -function, so P(X2) = 0 if X2 ≠ x2, and P(X2) = 1 when X2 = x2. We’re basically saying that when we intervene to set X2 = x2, we’re sure that it worked. We can carry through that X2 = x2 elsewhere, like in the distribution for P(X4|X2, X3), but just replacing X2 with X2 = x2, since the whole right-hand side is zero if X2 ≠ x2.
Finally, let’s just condition on the X2 distribution to get rid of the weirdness on the right-hand side of this formula. We can write the following:
)
However, this is the same as the original formula, divided by P(X2|X1)! To be precise,
)
Incredibly, this formula works in general. We can write the following:
)
This leads us to a nice general rule: the parents of a variable will always satisfy the back-door criterion! It turns out we can be more general than this even. If we marginalize out everything except Xi and Xj, we see the parents are the set of variables that control confounders.
)
It turns out (we’ll state without proof) that you can generalize the parents to any set, Z, that satisfies the back door criterion.
)
){kind=link}
){kind=link}
){kind=link}
You can marginalize Z out of this and use the definition of conditional probability to write an important formula, shown in Definition 13.3.
DEFINITION 13.3. ROBINS G-FORMULA
This is a general formula for estimating the distribution of Xj under the intervention Xi. Notice that all of these distributions are from the pre-intervention system. This means you can use observational data to estimate the distribution of Xj under some hypothetical intervention!
There are a few critical caveats here. First, the term in the denominator of Equation 13.4, P(Xi|Pa(Xi)), must be nonzero for the quantity on the left side to be defined. This means you would have to have observed Xi taking on the value you’d like to set it to with your intervention. If you’ve never seen it, you can’t say how the system might behave in response to it!
Next, you’re assuming that you have a set Z that you can control for. Practically, it’s hard to know if you’ve found a good set of variables. There can always be a confounder you have never thought to measure. Likewise, your way of controlling for known confounders might not do a very good job. You’ll understand this second caveat more as you go into some machine learning estimators.
With these caveats, it can be hard to estimate causal effects from observational data. You should consider the results of a conditioning approach to be a provisional estimate of a causal effect. If you’re sure you’re not violating the first condition of the back-door criterion, then you can expect that you’ve removed some spurious dependence. You can’t say for sure that you’ve reduced bias.
Imagine, for example, two sources of bias for the effect of Xi on Xj. Suppose you’re interested in measuring an average value of Xj, Edo(xi=xi)[Xj] = μj. Path A introduces a bias of−δ, and path B introduces a bias of 2δ. If you estimate the mean without controlling for either path, you’ll find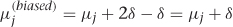 
. If you control for a confounder along path A, then you remove its contribution to the bias, which leaves 
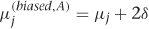. Now the bias is twice as large! The problem, of course, is that the bias you corrected was actually pushing our estimate back toward its correct value. In practice, more controlling usually helps, but you can’t be guaranteed that you won’t find an effect like this.
Now that you have a good background in observational causal inference, let’s see how machine-learning estimators can help in practice!