Updating the Game
Most video games have some concept of time progression. For real-time games, you measure this progression of time in fractions of a second. For example, a game running at 30 FPS has roughly 33 milliseconds (ms) elapse from frame to frame. Remember that even though a game appears to feature continuous movement, it is merely an illusion. The game loop actually runs several times per second, and every iteration of the game loop updates the game in a discrete time step. So, in the 30 FPS example, each iteration of the game loop should simulate 33ms of time progression in the game. This section looks at how to consider this discrete progression of time when programming a game.
Real Time and Game Time
It is important to distinguish real time, the time elapsing in the real world, from game time, the time elapsing in the game’s world. Although there often is a 1:1 correspondence between real time and game time, this isn’t always the case. Take, for instance, a game in a paused state. Although a great deal of time might elapse in the real world, the game doesn’t advance at all. It’s not until the player unpauses the game that the game time resumes updating.
There are many other instances where real time and game time might diverge. For example, some games feature a “bullet time” gameplay mechanic that reduces the speed of the game. In this case, the game time must update at a substantially slower rate than actual time. On the opposite end of the spectrum, many sports games feature sped-up time. In a football game, rather than requiring a player to sit through 15 full minutes per quarter, the game may update the clock twice as fast, so each quarter takes only 7.5 minutes. And some games may even have time advance in reverse. For example, Prince of Persia: The Sands of Time featured a unique mechanic where the player could rewind the game time to a certain point.
With all these ways real time and game time might diverge, it’s clear that the “update game” phase of the game loop should account for elapsed game time.
Logic as a Function of Delta Time
Early game programmers assumed a specific processor speed and, therefore, a specific frame rate. The programmer might write the code assuming an 8 MHz processor, and if it worked properly for those processors, the code was just fine. When assuming a fixed frame rate, code that updates the position of an enemy might look something like this:
// Update x position by 5 pixels enemy.mPosition.x += 5;
If this code moves the enemy at the desired speed on an 8 MHz processor, what happens on a 16 MHz processor? Well, because the game loop now runs twice as fast, the enemy will now also move twice as fast. This could be the difference between a game that’s challenging for players and one that’s impossible. Imagine running this game on a modern processor that is thousands of times faster. The game would be over in a heartbeat!
To solve this issue, games use delta time: the amount of elapsed game time since the last frame. To convert the preceding code to using delta time, instead of thinking of movement as pixels per frame, you should think of it as pixels per second. So, if the ideal movement speed is 150 pixels per second, the following code is much more flexible:
// Update x position by 150 pixels/second enemy.mPosition.x += 150 * deltaTime;
Now the code will work well regardless of the frame rate. At 30 FPS, the delta time is ~0.033, so the enemy will move 5 pixels per frame, for a total of 150 pixels per second. At 60 FPS, the enemy will move only 2.5 pixels per frame but will still move a total of 150 pixels per second. The movement certainly will be smoother in the 60 FPS case, but the overall per-second speed remains the same.
Because this works across many frame rates, as a rule of thumb, everything in the game world should update as a function of delta time.
To help calculate delta time, SDL provides an SDL_GetTicks member function that returns the number of milliseconds elapsed since the SDL_Init function call. By saving the result of SDL_GetTicks from the previous frame in a member variable, you can use the current value to calculate delta time.
First, you declare an mTicksCount member variable (initializing it to zero in the constructor):
Uint32 mTicksCount;
Using SDL_GetTicks, you can then create a first implementation of Game::UpdateGame:
void Game::UpdateGame()
{
// Delta time is the difference in ticks from last frame
// (converted to seconds)
float deltaTime = (SDL_GetTicks() - mTicksCount) / 1000.0f;
// Update tick counts (for next frame)
mTicksCount = SDL_GetTicks();
// TODO: Update objects in game world as function of delta time!
// ...
}
Consider what happens the very first time you call UpdateGame. Because mTicksCount starts at zero, you end up with some positive value of SDL_GetTicks (the milliseconds since initialization) and divide it by 1000.0f to get a delta time in seconds. Next, you save the current value of SDL_GetTicks in mTicksCount. On the next frame, the deltaTime line calculates a new delta time based on the old value of mTicksCount and the new value. Thus, on every frame, you compute a delta time based on the ticks elapsed since the previous frame.
Although it may seem like a great idea to allow the game simulation to run at whatever frame rate the system allows, in practice there can be several issues with this. Most notably, any game that relies on physics (such as a platformer with jumping) will have differences in behavior based on the frame rate.
Though there are more complex solutions to this problem, the simplest solution is to implement frame limiting, which forces the game loop to wait until a target delta time has elapsed. For example, suppose that the target frame rate is 60 FPS. If a frame completes after only 15ms, frame limiting says to wait an additional ~1.6ms to meet the 16.6ms target time.
Conveniently, SDL also provides a method for frame limiting. For example, to ensure that at least 16ms elapses between frames, you can add the following code to the start of UpdateGame:
while (!SDL_TICKS_PASSED(SDL_GetTicks(), mTicksCount + 16)) ;
You also must watch out for a delta time that’s too high. Most notably, this happens when stepping through game code in the debugger. For example, if you pause at a breakpoint in the debugger for five seconds, you’ll end up with a huge delta time, and everything will jump far forward in the simulation. To fix this problem, you can clamp the delta time to a maximum value (such as 0.05f). This way, the game simulation will never jump too far forward on any one frame. This yields the version of Game::UpdateGame in Listing 1.5. While you aren’t updating the position of the paddle or ball just yet, you are at least calculating the delta time value.
Listing 1.5 Game::UpdateGame Implementation
void Game::UpdateGame()
{
// Wait until 16ms has elapsed since last frame
while (!SDL_TICKS_PASSED(SDL_GetTicks(), mTicksCount + 16))
;
// Delta time is the difference in ticks from last frame
// (converted to seconds)
float deltaTime = (SDL_GetTicks() - mTicksCount) / 1000.0f;
// Clamp maximum delta time value
if (deltaTime > 0.05f)
{
deltaTime = 0.05f;
}
// TODO: Update objects in game world as function of delta time!
}
Updating the Paddle’s Position
In Pong, the player controls the position of the paddle based on input. Suppose you want the W key to move the paddle up and the S key to move the paddle down. Pressing neither key or both keys should mean the paddle doesn’t move at all.
You can make this concrete by using a mPaddleDir integer member variable that’s set to 0 if the paddle doesn’t move, -1 if if the paddle moves up (negative y), and 1 if the paddle moves down (positive y).
Because the player controls the position of the paddle via keyboard input, you need code in ProcessInput that updates mPaddleDir based on the input:
mPaddleDir = 0;
if (state[SDL_SCANCODE_W])
{
mPaddleDir -= 1;
}
if (state[SDL_SCANCODE_S])
{
mPaddleDir += 1;
}
Note how you add and subtract from mPaddleDir, which ensures that if the player presses both keys, mPaddleDir is zero.
Next, in UpdateGame, you can add code that updates the paddle based on delta time:
if (mPaddleDir != 0)
{
mPaddlePos.y += mPaddleDir * 300.0f * deltaTime;
}
Here, you update the y position of the paddle based on the paddle direction, a speed of 300.0f pixels/second, and delta time. If mPaddleDir is -1, the paddle will move up, and if it’s 1, it’ll move down.
One problem is that this code allows the paddle to move off the screen. To fix this, you can add boundary conditions for the paddle’s y position. If the position is too high or too low, move it back to a valid position:
if (mPaddleDir != 0)
{
mPaddlePos.y += mPaddleDir * 300.0f * deltaTime;
// Make sure paddle doesn't move off screen!
if (mPaddlePos.y < (paddleH/2.0f + thickness))
{
mPaddlePos.y = paddleH/2.0f + thickness;
}
else if (mPaddlePos.y > (768.0f - paddleH/2.0f - thickness))
{
mPaddlePos.y = 768.0f - paddleH/2.0f - thickness;
}
}
Here, the paddleH variable is a constant that describes the height of the paddle. With this code in place, the player can now move the paddle up and down, and the paddle can’t move offscreen.
Updating the Ball’s Position
Updating the position of the ball is a bit more complex than updating the position of the paddle. First, the ball travels in both the x and y directions, not just in one direction. Second, the ball needs to bounce off the walls and paddles, which changes the direction of travel. So you need to both represent the velocity (speed and direction) of the ball and perform collision detection to determine if the ball collides with a wall.
To represent the ball’s velocity, add another Vector2 member variable called mBallVel. Initialize mBallVel to (-200.0f, 235.0f), which means the ball starts out moving −200 pixels/second in the x direction and 235 pixels/second in the y direction. (In other words, the ball moves diagonally down and to the left.)
To update the position of the ball in terms of the velocity, add the following two lines of code to UpdateGame:
mBallPos.x += mBallVel.x * deltaTime; mBallPos.y += mBallVel.y * deltaTime;
This is like updating the paddle’s position, except now you are updating the position of the ball in both the x and y directions.
Next, you need code that bounces the ball off walls. The code for determining whether the ball collides with a wall is like the code for checking whether the paddle is offscreen. For example, the ball collides with the top wall if its y position is less than or equal to the height of the ball.
The important question is: what to do when the ball collides with the wall? For example, suppose the ball moves upward and to the right before colliding against the top wall. In this case, you want the ball to now start moving downward and to the right. Similarly, if the ball hits the bottom wall, you want the ball to start moving upward. The insight is that bouncing off the top or bottom wall negates the y component of the velocity, as shown in Figure 1.7(a). Similarly, colliding with the paddle on the left or wall on the right should negate the x component of the velocity.

Figure 1.7 (a) The ball collides with the top wall so starts moving down. (b) The y difference between the ball and paddle is too large
For the case of the top wall, this yields code like the following:
if (mBallPos.y <= thickness)
{
mBallVel.y *= -1;
}
However, there’s a key problem with this code. Suppose the ball collides with the top wall on frame A, so the code negates the y velocity to make the ball start moving downward. On frame B, the ball tries to move away from the wall, but it doesn’t move far enough. Because the ball still collides with the wall, the code negates the y velocity again, which means the ball starts moving upward. Then on every subsequent frame, the code keeps negating the ball’s y velocity, so it is forever stuck on the top wall.
To fix this issue of the ball getting stuck, you need an additional check. You want to only negate the y velocity if the ball collides with the top wall and the ball is moving toward the top wall (meaning the y velocity is negative):
if (mBallPos.y <= thickness && mBallVel.y < 0.0f)
{
mBallVel.y *= -1;
}
This way, if the ball collides with the top wall but is moving away from the wall, you do not negate the y velocity.
The code for colliding against the bottom and right walls is very similar to the code for colliding against the top wall. Colliding against the paddle, however, is slightly more complex. First, you calculate the absolute value of the difference between the y position of the ball and the y position of the paddle. If this difference is greater than half the height of the paddle, the ball is too high or too low, as shown earlier in Figure 1.7(b). You also need to check that the ball’s x-position lines up with the paddle, and the ball is not trying to move away from the paddle. Satisfying all these conditions means the ball collides with the paddle, and you should negate the x velocity:
if (
// Our y-difference is small enough
diff <= paddleH / 2.0f &&
// Ball is at the correct x-position
mBallPos.x <= 25.0f && mBallPos.x >= 20.0f &&
// The ball is moving to the left
mBallVel.x < 0.0f)
{
mBallVel.x *= -1.0f;
}
With this code complete, the ball and paddle now both move onscreen, as in Figure 1.8. You have now completed your simple version of Pong!
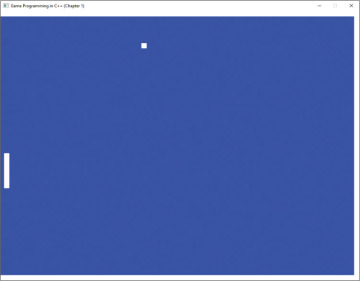
Figure 1.8 Final version of Pong

