- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.9 Characteristic Impedance and Controlled Impedance
For a uniform line, anywhere we choose to look, we will see the same instantaneous impedance as we propagate down the line. There is one instantaneous impedance that characterizes the transmission line, and we give it the special name: characteristic impedance.
To distinguish that we are referring of the special case of the characteristic impedance of the line, which is an intrinsic property of the line, we give it the special symbol Z0 (Z with a subscript zero). Characteristic impedance is given in units of Ohms. Every uniform transmission line has a characteristic impedance, which is one of the most important terms describing its electrical properties and how signals will interact with it.
Characteristic impedance is numerically equal to the instantaneous impedance of the line and is intrinsic to the line. It depends only on the dielectric constant and the capacitance per length of the line. It does not depend on the length of the line.
For a uniform line, the characteristic impedance is:
If the line is uniform, it has only one instantaneous impedance, which we call the characteristic impedance. One measure of the uniformity of the line is how constant the instantaneous impedance is down the length. If the line width varies down the line, there is no one single value of instantaneous impedance for the whole line. By definition, a nonuniform line has no characteristic impedance. When the cross section is uniform, the impedance a signal sees as it propagates down the interconnect will be constant, and we say the impedance is controlled. For this reason, we call uniform cross-section transmission lines controlled-impedance lines.
When the geometry and material properties are constant down the line, the instantaneous impedance of the line is uniform, and one number fully characterizes the impedance of the line.
A controlled-impedance line can be fabricated with virtually any uniform cross section. There are many standard cross-sectional shapes that can have controlled impedance, and many of these families of shapes have special names. For example, two round wires twisted together are called a twisted pair. A center conductor surrounded by an outer conductor is a coaxial, or coax, transmission line. A narrow strip of signal line over a wide plane is a microstrip. When the return path is two planes and the signal line is a narrow strip between them, we call this a stripline. The only requirement for a controlled-impedance interconnect is that the cross section be constant.
With this connection between the capacitance per length and the characteristic impedance, we can now relate our intuition about capacitance to our new intuition about characteristic impedance: What increases one will decrease the other.
We generally have a pretty good intuitive feel for capacitance and capacitance per length for the two conductors in a transmission line. If we make the two conductors wider, we increase the capacitance per length. This will decrease the characteristic impedance. If we move them farther apart, we make the capacitance per length lower and the characteristic impedance higher.
For a microstrip using FR4 dielectric, when the line width is twice the dielectric thickness, the characteristic impedance is about 50 Ohms. What happens to the characteristic impedance when we make the dielectric separation larger? It’s not obvious initially. However, we now know that the characteristic impedance of a transmission line is inversely proportional to the capacitance per length between the conductors.
Therefore, if we move the conductors farther apart, the capacitance will decrease, and the characteristic impedance will increase. Making the microstrip signal trace wider will increase the capacitance per length and decrease the characteristic impedance. This is illustrated in Figure 7-10.
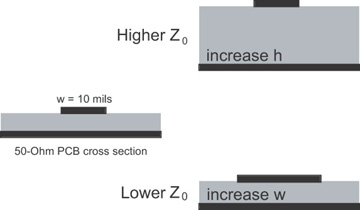
Figure 7-10 If line width increases, capacitance per length increases, and characteristic impedance decreases. If dielectric spacing increases, capacitance per length decreases, and characteristic impedance increases.
In general, a wide conductor with a thin dielectric will have a low characteristic impedance. For example, the characteristic impedance of the transmission line formed from the power and ground planes in a PCB will have a low characteristic impedance, generally less than 1 Ohm. Narrow conductors with a thick dielectric will have a high characteristic impedance. Signal traces with narrow lines will have high characteristic impedance, typically between 60 Ohms and 90 Ohms.


