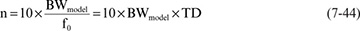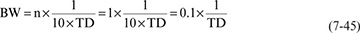- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.18 An n-Section Lumped-Circuit Model
The ideal transmission-line circuit element is a distributed element that very accurately predicts the measured performance of real interconnects. Figure 7-37 shows the comparison of the measured and simulated impedance of a 1-inch-long transmission line in the frequency domain. We see the excellent agreement even up to 5 GHz, the bandwidth of the measurement.
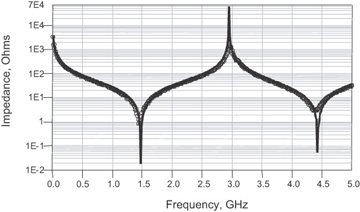
Figure 7-37 Measured (circles) and simulated (line) impedance of a 1-inch-long, 50-Ohm transmission line. The model is an ideal, lossless transmission line. The agreement is excellent up to the bandwidth of the measurement.
We can approximate this ideal model with a combination of LC lumped-circuit sections. How do we know how many LC sections to use for a given level of accuracy? What happens if we use too few sections?
These questions can be explored using a simulation tool like SPICE. We will first work in the frequency domain to evaluate the impedance by looking into the front end of a transmission line and then interpret this result in the time domain.
In the frequency domain, we can ask What is the impedance when looking into the front end of a transmission line, with the far end open? In this example, we will use a 50-Ohm line that is 6 inches long with a dielectric constant of 4. Its time delay, TD, is 1 nsec.
The total capacitance is given by Ctotal = TD/Z0 = 1 nsec/50 Ohms = 20 pF. The total loop inductance is given by Ltotal = Z0 × TD = 50 Ohms × 1 nsec = 50 nH.
The simplest approximation for a transmission line is a single LC model, with the L and C values as the total values of the transmission line. This is the simplest lumped-circuit model for an ideal transmission line.
Figure 7-38 shows the predicted impedance for an ideal, distributed transmission line and the calculated impedance of a single-section LC lumped-circuit model using these values. In the low-frequency range, the LC model matches the performance really well. The bandwidth of this model is about 100 MHz. The limitation to the bandwidth occurs because, in fact, this ideal transmission line does not have all its capacitance in one place. Instead, it is distributed down the length, and between each capacitor is some loop inductance associated with the length of the sections. However, it is clear from this comparison that a transmission line, open at the far end, will look exactly like an ideal capacitor at low frequency.
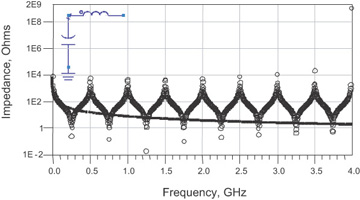
Figure 7-38 Simulated impedance of an ideal transmission line (circles) and simulated impedance of a single-section LC lumped-circuit model (line). The agreement is excellent up to bandwidth of about 100 MHz.
The impedance of the ideal transmission line shows the resonance peaks occurring when the frequency matches another half wavelength that can fit in the length of the transmission line. The peak resonant frequencies, fres, are given by:
where:
fres = frequency for the peaks in the impedance
m = number of the peak, also the number of half waves that fit in the transmission line
TD = time delay of the transmission line
f0 = frequency at which one complete wave fits in the transmission line
The first resonance for m = 1 is for 1 × 1 GHz/2 = 0.5 GHz. Here, just one half wave will fit evenly in the length of the transmission line, with a TD of 1 nsec. The second resonance for m = 2 is at 2 × 1 GHz/2 = 1 GHz. Here, exactly one wave will fit in the transmission line. These standing wave patterns are shown in Figure 7-39.
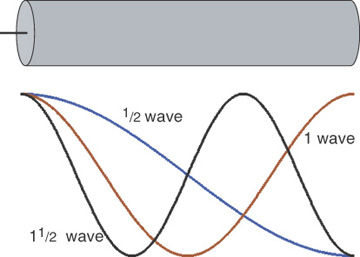
Figure 7-39 Voltage waves on the transmission line. Resonances occur when an additional half wavelength can fit in the line.
The bandwidth of the single-section LC model is about one-quarter the frequency of the first resonance, up to about 125 MHz. We can improve the bandwidth of the model by breaking the transmission line into more sections. If we break it up in two sections, each section can be modeled as an identical LC model, and the values of each L and C would be Ltotal/2 and Ctotal/2. The predicted impedance of this two-section LC model compared with the ideal T line is shown in Figure 7-40. The bandwidth of this model is roughly at half the first resonance peak. This is a frequency of about 250 MHz.
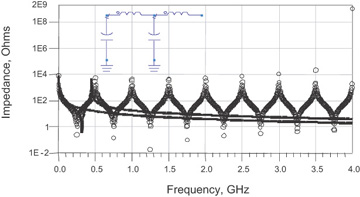
Figure 7-40 Simulated impedance of an ideal transmission line (circles) and simulated impedance of a one-section and two-section LC lumped-circuit model (lines).
We can further increase the bandwidth of this lumped-circuit model by breaking up the length into more LC sections. Figure 7-41 shows the comparison with an ideal transmission line and using 16 different LC sections, with each L and C being Ltotal/16 and Ctotal/16. As we increase the number of sections, we are able to better approximate, to a higher bandwidth, the impedance behavior of an ideal transmission line. The bandwidth of this model is about up to the fourth resonance peak, at 2 GHz.
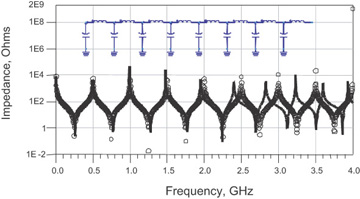
Figure 7-41 Simulated impedance of an ideal transmission line (circles) and simulated impedance of a 16-section LC lumped-circuit model (line).
We can estimate the bandwidth of an n-section lumped-circuit model based on the time delay of this ideal transmission line. These last examples illustrate that the more segments in the LC model, the higher the bandwidth. One section has a bandwidth up to one-quarter of the first resonant peak; 2 sections up to half the first resonance; and 16 sections up to the second resonant frequency. We can generalize that the highest frequency at which we have good agreement—the bandwidth of the model—is:
or:
where:
BWmodel = bandwidth of the n-section lumped-circuit model
n = number of LC sections in the model
TD = time delay of the transmission line
f0 = resonant frequency for one complete wavelength = 1/TD
We have approximated the relationship to be a little more conservative and a little easier to remember by using n = 10 × BWmodel × TD rather than n = 8 × BWmodel × TD.
For example, if the interconnect has a TD = 1 nsec, and we would like an n-section LC model with a bandwidth of 5 GHz, then we need at least n = 10 × 5 GHz × 1 nsec = 50 sections. At this highest frequency, there will be 5 GHz × 1 nsec = 5 wavelengths on the transmission line. For each wave, we need 10sections; therefore, we need 5 × 10 = 50 LC sections for a good approximation.
If the TD of a line is 0.5 nsec, and we need a bandwidth of 2 GHz, the number of sections required is n = 10 × 2 GHz × 0.5 nsec = 10 sections.
We can also evaluate the frequency to which we can use a single LC section to model a transmission line. In other words, up to what frequency does a transmission line look like a simple LC circuit? The bandwidth of one section is:
For the case of a transmission line with TD = 1 nsec, the bandwidth of a single-section LC model for this line is 0.1 × 1/1 nsec = 100 MHz. If TD = 0.16 nsec (roughly 1 inch long), the bandwidth of a simple LC model for this line is 0.1 × 1/0.16 nsec = 600 MHz. The longer the time delay of a transmission line, the lower the frequency at which we can approximate it as a simple LC model.
In evaluating the number of sections we need to describe a transmission line for a required bandwidth, we have found that we needed about 10 LC sections per wavelength of the highest-frequency component of the signal and a total number of LC segments depending on the number of wavelengths of the highest frequency component of the signal that can fit in the transmission line.
If we have a signal with a rise time, RT, the bandwidth associated with the signal (the highest-sine-wave frequency component that is significant) is BWsig = 0.35/RT. If we have a transmission line that has a time delay of TD, and we wish to approximate it with an n-section lumped-circuit model, we need to make sure the bandwidth of the model, BWmodel, is at least > BWsig:
where:
BWsig = bandwidth of the signal
BWmodel = bandwidth of the model
RT = rise time of the signal
TD = time delay of the transmission line
n = minimum number of LC sections needed for an accurate model
For example, with a rise time of 0.5 nsec and time delay of 1 nsec, we would need n > 3.5 × 1/0.5 = 7 sections for an accurate model.
When the rise time is equal to the TD of the line we want to model, we need at least 3.5 sections for an accurate model. In this case, the spatial extent of the rise time is the length of the transmission line. This suggests a very important rule of thumb, given in the following tip.
This rule of thumb is illustrated in Figure 7-42. In FR4, if the rise time is 1 nsec, the spatial extent of the leading edge is 6 inches. We need 3.5 LC sections for every 6 inches of length, or about 1.7 inches per section. We can generalize this: If the rise time is RT, and the speed of the signal is v, then the length for each LC section is (RT × v)/3.5. In FR4, where the speed is about 6 inches/nsec, the length of each LC section required for a rise time, RT, is 1.7 × RT, with rise time in nsec.
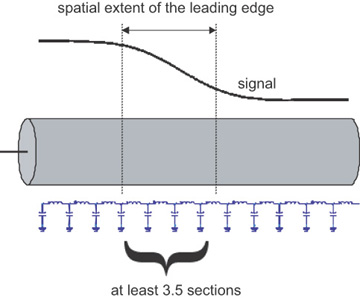
Figure 7-42 As a general rule of thumb, there should be at least 3.5 LC sections per spatial extent of the rise time for an accurate model of the interconnect at the bandwidth of the signal.
If the rise time is 1 nsec, the length of each single LC should be less than 1.7 inches. If the rise time is 0.5 nsec, the length of each LC section should be no longer than 0.5 × 1.7 = 0.85 inches.
The analysis in this section evaluated the minimum number of many LC sections required to model a real transmission with adequate accuracy up to the bandwidth of the signal. But this is still an approximation with limited bandwidth. This is why the first choice when selecting a model for a real transmission line should always be an ideal transmission line, defined by a characteristic impedance and time delay. Only under very rare conditions, when the question is phrased in terms of the L or C values, should an n-section lumped model ever be used to model a real transmission line. Always start with an ideal transmission-line model.