- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.17 Calculating the Characteristic Impedance with a 2D Field Solver
If we need better than 10% accuracy or are worrying about second-order effects, such as the effect of trace thickness, solder-mask coverage, or side-wall shape, we should not be using one of these approximations. The most important tool that should be in every engineer’s toolbox for doing impedance calculations is a 2D field solver.
The basic assumption made by all 2D field solvers is that the geometry is uniform down the length of the line. That is, as we move down the length of the transmission line, the cross-sectional geometry stays the same. This is the basic definition of a controlled-impedance line—that the cross section is uniform. In such a case, there is only one characteristic impedance that describes the line. This is why a 2D field solver is the right tool to provide an accurate prediction of the characteristic impedance of uniform transmission lines. Only the 2D cross-sectional information is important.
Whenever accuracy is important, a 2D field solver should be used. This means that before sign-off on a design and committing to hardware, the stack-up should be designed with a 2D field solver. Sometimes the argument is made that if the manufacturing tolerance is 10%, we should not care if the accuracy of the prediction is even 5%.
Accuracy is important because of yield. Any inaccuracy in the predicted impedance will shift the center position of the distribution of the manufactured impedances. The better we can center the distribution on the required target, the better we can increase yield. Even an inaccuracy of 1% will shift the distribution off center. Any product close to the spec limits could be shifted outside the limits and contribute to a yield hit. As we showed in Chapter 5, the accuracy of a field solver can be better than 0.5%.
By using a 2D field solver, the characteristic impedance of a microstrip can be calculated. These results are compared to the predictions based on the IPC approximations. Figure 7-32 shows the predicted characteristic impedance of a microstrip with dielectric constant of 4, with 1/2-ounce copper and dielectric thickness of 10 mils, as the line width is varied. Near and above 50 Ohms, the agreement is very good. However, for lower impedances, the IPC approximation can be off by as much as 25%.
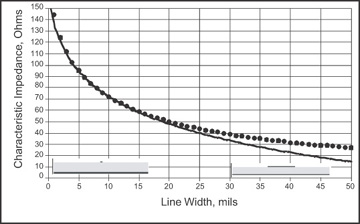
Figure 7-32 Comparison of field-solver results (circles) and the IPC approximation (line) for a microstrip with 10-mil-thick FR4 dielectric and 1/2-ounce copper. Field-solver results from the Ansoft 2D Extractor.
The same comparison is made for stripline and is shown in Figure 7-33. The agreement close to 50 Ohms is very good, but for low impedances, the approximation can be off by more than 25%. Approximations should not be used when accuracy counts.
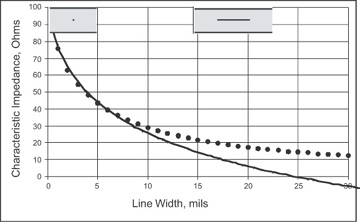
Figure 7-33 Comparison of field-solver results (circles) and the IPC approximation (line) for a stripline with 10-mil-thick FR4 dielectric and 1/2-ounce copper. Field-solver results from the Ansoft 2D Extractor.
In addition to providing an accurate estimate for the characteristic impedance, a 2D field solver can also provide insight into the impact from second-order effects, such as:
The width of the return path
The thickness of the signal-trace conductor
The presence of solder mask over a surface trace
The effective dielectric constant
How does the width of the return path influence the characteristic impedance? Applying the principles of Bogatin’s rule 9, we would anticipate that if the width of the return path is narrow, the capacitance should be smaller and the characteristic impedance higher. Using a field solver, we can calculate how wide the return path has to be so that it doesn’t matter anymore.
Figure 7-34 shows the calculated characteristic impedance of a microstrip with dielectric constant of 4 and trace thickness of 0.7 mil, corresponding to 1/2-ounce copper, dielectric thickness of 5 mils, and line width of 10 mils. This is nominally a 50-Ohm line. The width of the return path is varied and the characteristic impedance calculated. If the width of the extension on each side of the signal trace is greater than 15 mils, the characteristic impedance is less than 1% off from its infinite-width value. Because the fringe fields along the edge of the trace scale with the dielectric thickness, this is the important scale factor. The extent of the return path on either side of the signal path should be roughly three times the dielectric thickness, h.
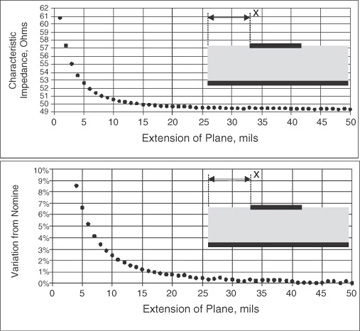
Figure 7-34 Top: Calculated characteristic impedance of a microstrip with 10-mil-wide trace and 5-mil-thick dielectric, as the return-path plane is widened. Bottom: Variation from the nominal value. Field-solver results from the Ansoft 2D Extractor.
Again following rule 9, we would anticipate that as trace thickness increases, there will be more fringe fields coming off the sides, and the capacitance per length would increase. This would make the characteristic impedance lower as the conductor thickness increases.
Using a 2D field solver, we can calculate the characteristic impedance as the trace thickness changes from 0.1 mil thick to 3 mils thick. This is plotted in Figure 7-35. Each point on the curve is the calculated characteristic impedance for a different trace thickness. Sure enough, as the metal thickness increases, the fringe field capacitance increases, and the characteristic impedance decreases. Thicker metal means higher capacitance between the signal trace and the return path, which also means lower characteristic impedance. However, as we can see from the calculated results, this is not a large effect; it is second order.
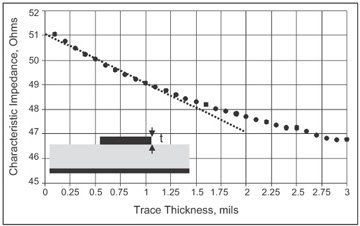
Figure 7-35 Calculated characteristic impedance of a nominal 50-Ohm microstrip as the trace thickness is changed. The circles are calculated results; the line is 2 Ohms/mil. Field-solver results from the Ansoft 2D Extractor.
If there is a thin solder-mask coating on top of the microstrip, the fringe field capacitance should increase, and the characteristic impedance should decrease. For the same microstrip as above, but using a conductor only 0.1 mil thick, the characteristic impedance is calculated for an increasing solder-mask coating, using a dielectric constant of 4. Figure 7-36 shows the decrease in characteristic impedance. It is about 2 Ohms/mil of coating for thin coatings. After about 10-mil-thick coating, the characteristic impedance is no longer affected, as all the external fringe fields are contained in the first 10 mils of coating. This is a measure of how far the fringe fields extend above the surface.
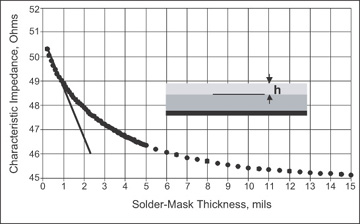
Figure 7-36 Calculated characteristic impedance of a nominal 50-Ohm microstrip as a solder mask with dielectric constant of 4 is added. Circles are the field-solver results; the line is 2 Ohms/mil. Field-solver results from the Ansoft 2D Extractor.
Of course, solder mask is more typically 0.5 mil to 2 mils. In this regime, we see that the presence of the solder mask can lower the characteristic impedance by as much as 2 Ohms—a significant amount. Reaching a target impedance with solder mask requires the line width to be narrower than nominal, so the solder mask would bring the impedance back down to the target value.
This last example illustrates that the characteristic impedance depends on the dielectric distribution above the trace in a microstrip. Of course, in a stripline, all the fields are contained by the dielectric, so solder mask on top of the upper plane has no impact on the characteristic impedance.
In addition to the characteristic impedance affected by the inhomogeneous dielectric distribution, the effective dielectric constant that the fields experience is also affected by the dielectric distribution. In microstrip, the effective dielectric constant, which determines the speed of the signal, depends on the specific geometry of the dielectric. Often, the effective dielectric constant can be accurately calculated only with a field solver. This was discussed in detail in Chapter 5.

