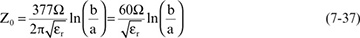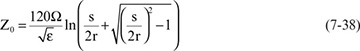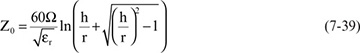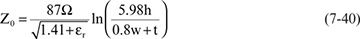- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.16 Calculating Characteristic Impedance with Approximations
Engineering a particular target characteristic impedance is really a matter of adjusting the line widths, dielectric thickness, and dielectric constants. If we know the length of the transmission line and the dielectric constant of the material around the conductors and we can calculate the characteristic impedance, we can use the relationships above to calculate all other parameters.
Of course, every different type of cross-sectional geometry will have a different relationship between the geometrical features and the characteristic impedance. In general, there are three types of analysis we can use to calculate the characteristic impedance from the geometry:
Rules of thumb
Approximations
2D field solvers
The two most important rules of thumb relate the characteristic impedance of a microstrip and stripline fabricated with FR4. The cross sections for 50-Ohm transmission lines are illustrated in Figure 7-30.
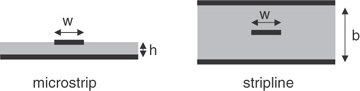
Figure 7-30 Scaled cross sections for 50-Ohm transmission lines in FR4. Left: 50-Ohm microstrip with w = 2 × h. Right: 50-Ohm stripline with b = 2 × w.
There are only three cross-section geometries that have exact equations: coax, twin-round-wire, and round-wire-over-plane geometries (see Figure 7-31). All others are approximations. The relationship between characteristic impedance and geometry for coax is:
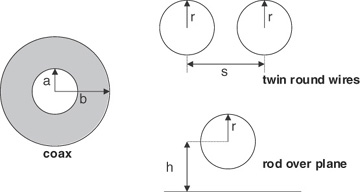
Figure 7-31 The only three cross sections for which there are exact equations for the characteristic impedance. All others are approximations.
For twin parallel round wires, the characteristic impedance is:
For the case of a round rod over a plane, the characteristic impedance is:
where:
Z0 = characteristic impedance, in Ohms
a = inner radius of the coax, in inches
b = outer radius of the coax, in inches
r = radius of the round rod, in inches
s = center-to-center spacing of the round rod, in inches
h = height of the center of the rod over the plane, in inches
εr = dielectric constant of the materials
These relationships assume that the dielectric material completely and uniformly fills all space wherever there are electric fields. If this is not the case, the effective dielectric constant that affects the speed of the signal down the conductor will be some complicated combination of the mixture of dielectrics. This can often be calculated only with a field solver.
For homogeneous dielectric distributions, these are useful relationships to use to calibrate 2D field solvers since they are exact.
The value of approximations is that they show the relationship between the geometrical terms and can be used for sensitivity analysis in a spreadsheet. The most popular approximation for microstrip recommended by the IPC is:
For stripline, the IPC recommended approximation is:
where:
Z0 = characteristic impedance, in Ohms
h = dielectric thickness below the signal trace to the plane, in mils
w = line width, in mils
b = plane-to-plane spacing, in mils
t = metal thickness, in mils
εr = dielectric constant
If we ignore the impact from the trace thickness, t, then the characteristic impedance for both structures depends only on the ratio of the dielectric thickness to the line width. This is a very important relationship.
For example, if the line width is doubled and the dielectric spacing is doubled, the characteristic impedance, as a first-order approximation, will be unchanged.
Though these equations look complicated, this is no measure of their accuracy. The only way to know the accuracy of an approximation is to compare it to the results from a verified field solver.