- Calculating the Mean
- Calculating the Median
- Calculating the Mode
- From Central Tendency to Variability
Calculating the Median
The median of a group of observations is usually, and somewhat casually, thought of as the middle observation when they are in sorted order. And that’s usually a good way to think of it, even if it’s a little imprecise.
It’s often said, for example, that half the observations lie below the median while half lie above it. The Excel documentation says so. So does my old college stats text. But no. Suppose that your observations consist of the numbers 1, 2, 3, 4, and 5. The middlemost number in that set is 3. But it is not true that half the numbers lie above it or below it. It is accurate to state that the same number of observations lie below the median as lie above it. In the prior example, two observations lie below 3 and two lie above 3.
If there is an even number of observations in the data set, then it’s accurate to say that half lie below the median and half above it. But with an even number of observations there is no specific, middle record, and therefore there is no identifiable median record. Add one observation to the prior set, so that it consists of 1, 2, 3, 4, 5, and 6. There is no record in the middle of that set. Or make it 1, 2, 3, 3, 3, and 4. Although one of the 3s is the median, there is no specific, identifiable record in the middle of the set.
One way, used by Excel, to calculate the median with an even number of records is to take the mean of the two middle numbers. In this example, the mean of 3 and 4 is 3.5, which Excel calculates as the median of 1, 2, 3, 4, 5, and 6. And then, with an even number of observations, exactly half the observations lie below and half above the median. But 3.5 is not a member of the set.
The syntax for the MEDIAN() function echoes the syntax of the AVERAGE() function. For the data shown in Figure 2.7, you just enter this formula:
= MEDIAN(A2:A61)
Choosing to Use the Median
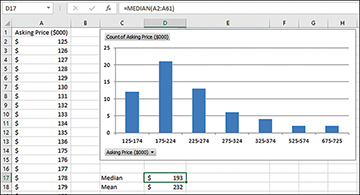
The median is sometimes a more descriptive measure of central tendency than the mean. For example, Figure 2.7 shows what’s called a skewed distribution—that is, the distribution isn’t symmetric. Most of the values bunch up on the left side, and a few are located off to the right (of course, a distribution can skew either direction—this one happens to skew right). This sort of distribution is typical of home prices and it’s the reason that the real estate industry reports medians instead of means.
In Figure 2.7, notice that the median home price reported is $193,000 and the mean home price is $232,000. The median responds only to the number of ranked observations, but the mean also responds to the size of the observations’ values.
Suppose that in the course of a week the price of the most expensive house increases by $100,000 and there are no other changes in housing prices. The median remains where it was, because it’s still at the 50th percentile in the distribution of home prices. It’s that 50% rank that matters, not the dollars associated with the most expensive house—or, for that matter, the cheapest.
In contrast, the mean would react if the most expensive house increased in price. In the situation shown in Figure 2.7, an increase of $120,000 in just one house’s price would increase the mean by $2,000—but the median would remain where it is.
The median’s relatively static quality is one reason that it’s the preferred measure of central tendency for housing prices and similar data. Another reason is that when distributions are skewed, the median can provide a better measure of how things tend centrally. Have another look at Figure 2.7. Which statistic seems to you to better represent the typical home price in that figure: the mean of $232,000 or the median of $193,000? It’s a subjective judgment, of course, but many people would judge that $193,000 is a better summary of the prices of these houses than is $232,000.
Static or Robust?
Since the middle of the last century, three particular concepts in statistics occasionally get hot and generate considerable discussion in journals and books, in blogs, and in classrooms. I’ll touch on these concepts from time to time in the remainder of this book. The concepts are robust statistics, nonparametric procedures, and distribution-free tests. The topics that the concepts address are very different from one another, but for various reasons writers and students tend to conflate them. I’ll try to draw the distinctions between them a little more finely in this book.
The topic of robust statistics is pertinent here because the nature of a distribution of values, as two prior sections have discussed, can cause you to prefer the mean or the median as the measure of central tendency of those values. This chapter has suggested that you prefer the median when the underlying distribution is skewed or asymmetric, and the mean otherwise.
In this context, the median has been termed a robust statistic because it tends to be unaffected by a change in one or more of the values used in its calculation. One or more values must cross the median, from the lower 50% to the upper 50%, or vice versa, for the value of the median to change. In contrast, the smallest change in any underlying value automatically changes the mean of the distribution.
This characteristic of the median has led some statisticians to refer to the median as robust. The term robust connotes a positive attribute. Something that is robust is thought of as strong, healthy, and hearty. For example, the following quote has been taken from a web page that promotes the use of the median in all cases, not just those that involve asymmetric distributions. If you look, you’ll find statements such as this: “The non-robust mean is susceptible to outliers, but the robust median is not affected by outliers.”
The very use of terms such as robust and susceptible tends to characterize the median as the method of choice. Note how easy it is to make the opposite point by replacing a couple of terms with near-synonyms: “The dynamic mean responds reliably to outliers, but the unresponsive median remains static.”
Some students read that sort of material, take note of the use of the word robust, and conclude that it’s easier and perhaps wiser to always use the median in preference to mean. That sort of thinking tends to drag along with it the distantly related concepts of nonparametric procedures and distribution-free tests.
But although there can be good reasons to choose the median rather than the mean, you should not automatically choose the median just because someone has termed it “robust.” You are likely to see other mistaken interpretations of nonparametrics and of distribution-free tests, and this book will discuss them as they arise in subsequent chapters.