- 1.1 What Is Mass Transfer?
- 1.2 Preliminaries: Continuum and Concentration
- 1.3 Flux Vector
- 1.4 Concentration Jump at Interface
- 1.5 Application Examples
- 1.6 Basic Methodology of Model Development
- 1.7 Conservation Principle
- 1.8 Differential Models
- 1.9 Macroscopic Scale
- 1.10 Mesoscopic or Cross-Section Averaged Models
- 1.11 Compartmental Models
- Summary
- Review Questions
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.8 Differential Models
In differential models, a differential control volume (e.g., a box with sides Δx, Δy, and Δz for Cartesian coordinates) is used to develop the transport models. The control volume is then made to tend to zero, thereby producing a set of differential equations for the primary field variable—namely, the concentration. These equations represent models at the highest level of hierarchy and contain the detailed information.
The simplest differential control volume is the one constructed in Cartesian coordinate volumes, which is shown in Figure 1.9. The net generation and accumulation depend on the control volume and, therefore, are known as volumetric terms. The net efflux term, known as the surface term, depends on the combined flux at that control surface. Application of the conservation principle, then, leads to the species mass balance equation involving the unknown fluxes. Nevertheless, this equation alone is not sufficient: We need additional relations because we ultimately want to solve for the concentration field. The flux term in the equation is the combined flux, which is the sum of the convection flux and the diffusion flux. The convection flux depends on the local velocity and local concentration, so it can be calculated if the velocity profile in the system is known. The diffusion flux results from the molecular interactions, which are not modeled at the continuum level. Hence a closure equation—that is, a constitutive model for diffusion— is needed to close the model. The most commonly used constitutive model is some form of Fick’s law. Note that for multicomponent diffusion in mixtures, the Stefan-Maxwell model for diffusion is also used; it is discussed in detail in Chapter 15.
)
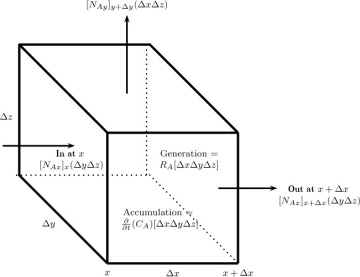
Figure 1.9 Differential control volume in Cartesian coordinates.
Note: Flux components from the hidden faces are not shown to avoid clutter.
In summary, mass transfer models at the differential levels are built through the combination of the conservation law and the constitutive law. The differential equations of mass transfer based on this approach are derived using this methodology in Chapter 5 and have general applicability. Many simpler problems can be deduced by simplification of these equations. In essence, this method is similar to that used in fluid mechanics, where the Navier-Stokes equations have general applicability for modeling flow of Newtonian fluids and where solutions to specific problems such as pipe flow can be obtained by simplification of these general equations. Likewise, we can go from the general to the particular in modeling of mass transfer. However, for simpler cases where the concentration varies only along one coordinate direction, it is instructive to derive and solve the equation by starting directly from the conservation laws and then using Fick’s law, rather than by directly using the general differential equations. This approach is illustrated in Chapter 2 for some common problems in mass transfer. A careful study of Chapter 2 will provide you with a basic understanding of the process of setting up and solving differential models.