- 5.1 Frequency-Flat Wireless Channels
- 5.2 Equalization of Frequency-Selective Channels
- 5.3 Estimating Frequency-Selective Channels
- 5.4 Carrier Frequency Offset Correction in Frequency-Selective Channels
- 5.5 Introduction to Wireless Propagation
- 5.6 Large-Scale Channel Models
- 5.7 Small-Scale Fading Selectivity
- 5.8 Small-Scale Channel Models
- 5.9 Summary
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.8 Small-Scale Channel Models
Because of the challenges associated with time selectivity, wireless communication systems are normally engineered such that the channel is time invariant over a packet, frame, block, or burst (different terminology for often the same thing). This is generally called fading. Even in such systems, though, the channel may still vary from frame to frame. In this section, we describe stochastic small-scale fading models. These models are used to describe how to generate multiple realizations of a channel for analysis or simulation. First, we review some models for flat fading, in particular Rayleigh, Ricean, and Nakagami fading. Then we review some models for frequency-selective fading, including a generalization of the Rayleigh model and the Saleh-Valenzuela clustered channel model. We conclude with an explanation about how to compute a bound on the average probability of symbol error in a flat-fading channel.
5.8.1 Flat-Fading Channel Models
In this section, we present different models for flat-fading channels. We focus on the case where the channel hs is a random variable that is drawn independently from frame to frame. We provide some explanation about how to deal with correlation over time at the end.
The most common model for flat fading is the Rayleigh channel model. In this case, hs has distribution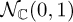 
. The variance is selected so that 
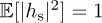, so that all gain in the channel is added by the large-scale fading channel. This is called the Rayleigh model because the envelope of the channel |hs| has the Rayleigh distribution, in this case given by fhs(x) = 2x exp(−x2). The magnitude squared |hs|2 is the sum of the squares of two N(0, 1/2) random variables, giving it a (scaled due to the 1/2) chi-square distribution. The channel phase (hs) is uniformly distributed on [0, 2π]. The Rayleigh fading channel model is said to model the case where there is a rich scattering NLOS environment. In this case, paths arrive from all different directions with slightly different phase shifts, and based on the central limit theorem, the distribution converges to a Gaussian.
Sometimes there is a dominant LOS path. In these cases, the Ricean channel model is used, parameterized by the K-factor. In the Ricean model, hs has distribution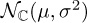 
. The Rice factor is K = |µ|2/σ2. Enforcing 
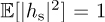, then µ2 + σ2 = 1. Substituting for µ2 = σ2K and simplifying leads to 
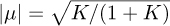and σ2 = 1/(1 + K). Then, in terms of K, hs has distribution 
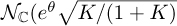where θ = phase(µ), but in most cases θ = 0 is selected. The Rice factor varies from K = 0 (corresponding to the Rayleigh case) to K = ∞ (corresponding to a non-fading channel).
Other distributions are used as well, inspired by measurement data, to give a better fit with observed data. The most common is the Nakagami-m distribution, which is a distribution for |hs| with an extra parameter m, with m = 1 corresponding to the Rayleigh case. The phase of hs is taken to be uniform on [0, 2π]. The Nakagami-m distribution is
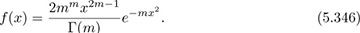
When |hs| is Nakagami-m, |hs|2 has a gamma distribution Γ(m, 1/m). The gamma distribution with two parameters is also used to give further flexibility for approximating measured data.
Time selectivity can also be incorporated into flat-fading models. This is most commonly done for the Rayleigh fading distribution. Let hs[n] denote the small-scale fading distribution as a function of n. In this case, n could index symbols or frames, depending on whether the channel is being generated in a symbol-by-symbol fashion or a frame-by-frame fashion. For purposes of illustration, we generate the channel once per Ntot symbols.
Suppose that we want to generate data with spatial correlation function RDoppler(Δtime). Let RDoppler[k] = RDoppler(kTNtot) be the equivalent discrete-time correlation function. We can generate a Gaussian random process with correlation function RDoppler[k] by generating an IID Gaussian random process with 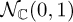and filtering that process with a filter q[k] such that RDoppler[k] = q[k] * q*[−k]. Such a filter can be found using algorithms in statistical signal processing [143]. It is often useful to implement the convolution by representing the filters in terms of their poles and zeros. For example, the coefficients of an all-pole IIR filter can be found by solving the Yule-Walker equations using the Levinson-Durbin recursion. The resulting channel would then be considered an autoregressive random process [19]. Other filter approximations are also possible, for example, using an autoregressive moving average process [25].
There are also deterministic approaches for generating random time-selective channels. The most widely known approach is Jakes’s sum-of-sinusoids approach [165], as a way to generate a channel with approximately the Clarke-Jakes Doppler spectrum. In this case, a finite number of sinusoids are summed together, with the frequency determined by the maximum Doppler shift and a certain amplitude profile. This approach was widely used with hardware simulators. A modified version with a little more randomness improves the statistical properties of the model [368].
5.8.2 Frequency-Selective Channel Models
In this section, we present different models for frequency-selective fading channels, focusing on the case where the channel coefficients are generated independently for each frame. Unlike in the previous section, we present two classes of models. Some are defined directly in discrete time. Others are physical models generated in continuous time, then converted to discrete time.
The discrete-time frequency-selective Rayleigh channel is a generalization of Rayleigh fading. In this model, the variance of the taps changes according to the specified symbol-spaced power delay profile Rdelay[ℓ] = Rdelay(ℓT). In this model hs[ℓ] is distributed as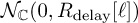 
. A special case of this model is the uniform power delay profile where hs[ℓ] is distributed as 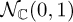, which is often used for analysis because of its simplicity. Sometimes the first tap has a Ricean distribution to model an LOS component.
Note that the total power in the channel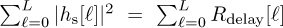 
, which depending on the power delay profile may be greater than 1. This is realistic because the presence of multiple paths allows the receiver to potentially capture more energy versus a flat-fading channel. Sometimes, though, the power delay profile may be normalized to have unit energy, which is useful when making comparisons with different power delay profiles.
Another class of frequency-selective channel models forms what are known as clustered channel models, the first of which is the Saleh-Valenzuela model [285]. This is a model for a continuous-time impulse response based on a set of distributions for amplitudes and delays and is a generalization of the single-path and two-path channels used as examples in Section 3.3.3. The complex baseband equivalent channel is
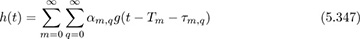
where Tm is the cluster delay, αm,q is the complex path gain, and τm,q is the path delay. The discrete-time equivalent channel is then given using the calculations in Section 3.3.5 as
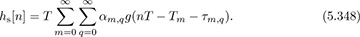
The choice of g(t) depends on exactly where the channel is being simulated. If the simulation only requires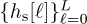 
obtained after matched filtering and sampling, then choosing g(t) = gtx(t) * grx(t) makes sense. If the channel is being simulated with oversampling prior to symbol synchronization and matched filtering, then alternatively it may make sense to replace q(t) with a lowpass filter with bandwidth corresponding to the bandwidth of x(t). In this case, the discrete-time equivalent may be obtained through oversampling, for example, by T/Mrx.
The Saleh-Valenzuela model is inspired by physical measurements that show that multipaths tend to arrive in clusters. The parameter Tm denotes the delay of a cluster, and the corresponding τm,q denotes the qth ray from the mth cluster.
The cluster delays are modeled as a Poisson arrival process with parameter Φ. This means that the interarrival distances Tm − Tm−1 are independent with exponential distribution f(Tm|Tm−1) = Φexp(−Φ(Tm − Tm−1)). Similarly, the rays are also modeled as a Poisson arrival process with parameter ϕ, giving τm,ℓ−τm,ℓ−1 an exponential distribution. The parameters Φ and ϕ would be determined from measurements.
The gains αm,q are complex Gaussian with a variance that decreases exponentially as the cluster delay and the ray delay increase. Specifically, αm,q is distributed as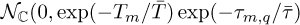 
where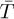 
and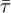 
are also parameters in the model.
The Saleh-Valenzuela model is distinctive in that it facilitates simulations with two scales of randomness. The first scale is in the choice of clusters and rays. The second scale is in the variability of the amplitudes over time. A simulation may proceed as follows. First, the cluster delays {Tm} and the associated ray delays τm,q are generated from the Poisson arrival model. For this given set of clusters and rays, several channel realizations may be generated. Conditioned on the cluster delays and ray delays, these channel coefficients are generated according to the power delay profile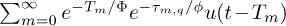 
where u(t) is the unit step function. In practical applications of this model, the number of rays and clusters is truncated, for example, ten clusters and 50 rays per cluster.
The impulse-based channel model in (5.347) can be used in other configurations, with or without clusters. For example, given a model of a propagation environment, ray tracing could be used to determine propagation paths, gains, and delays between a transmitter and a receiver. This information could be used to generate a channel model through (5.347). The model could be updated by moving a user through an area. In another variation, the cluster locations are determined from ray tracing, but then the rays arriving from each cluster are assumed to arrive randomly with a certain distribution (usually specified by the angle spread) [37, 38]. Other variations are possible.
There are different ways to incorporate mobility into a frequency-selective channel model. In the case of the discrete-time frequency-selective Rayleigh channel, the same approaches can be used as in the flat-fading case, but applied per tap. For example, each tap could be filtered so that every tap has a specified temporal correlation function (usually assumed to be the same). In the case of the Saleh-Valenzuela model, the clusters and rays could also be parameterized with an angle in space, and a Doppler shift derived from that angle. This could be used to model a time-varying channel given a set of clusters and rays.
5.8.3 Performance Analysis with Fading Channel Models
The coherence time and the coherence bandwidth, along with the corresponding signal bandwidth and sample period, determine the type of equivalent input-output relationship used for system design. Given a fading channel operating regime, an appropriate receiver can be designed based on system considerations, including the target error rate. The impact of fading on the system performance, though, depends on the discrete-time channel and the receiver processing used to deal with fading.
In complicated system design problems, as is the case in most standards-based systems, performance of the system is typically estimated using Monte Carlo simulation techniques. Essentially, this involves generating a realization of the fading channel, generating a packet of bits to transmit, generating additive noise, and processing the corresponding received signal.
For some special cases, though, it is possible to use a stochastic description of the channel to predict the performance without requiring simulation. This is useful in making initial system design decisions, followed up by more detailed simulations. In this section, we provide an example of the analysis of the probability of symbol error.
Consider a flat-fading channel described as
where we assume the large-scale fading is G = Ex. When the channel is modeled as a random variable, the instantaneous probability of symbol error rate written as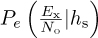 
is also a random variable. One measure of performance in this case is the average probability of symbol error. Other measures based on a notion of outage are also possible. The average probability of error is written as
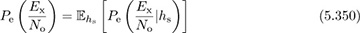
where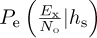 
is the probability of symbol error conditioned on a given value of hs. The expectation is taken with respect to all channels in the distribution to give
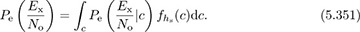
Note that we indicate this as a single integral, but since the channel is complex, it is more general to have a double integral. Given a prescribed fading channel model and probability of symbol error expression, the expectation or a bound can sometimes be calculated in closed form.
In this section, we calculate the expectation of the union bound on the probability of symbol error in an AWGN channel. Using the union bound,
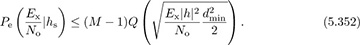
While solutions exist to help calculate the Q(·) function, such as Craig’s formula [80], a simpler method is to use the Chernoff bound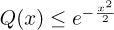 
. This gives
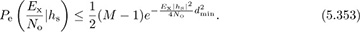
To proceed, we need to specify a distribution for the channel.
Suppose that the channel has the Rayleigh distribution. A way to evaluate (5.353) is to use the fact that hs is 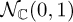and that any distribution function integrates to 1. Then, substituting in for fhs(c) = π−1 exp(−|c|2), it follows that
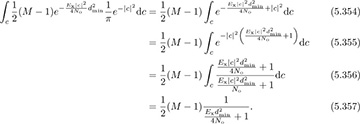
Putting it all together:
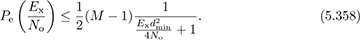
Example 5.34 Compute the Chernoff upper bound on the union bound for Rayleigh fading with M-QAM.
Answer: For M-QAM, we can insert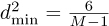 
into (5.358) to obtain
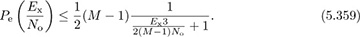
This provides somewhat more intuition than the exact solution, computed in [310] as
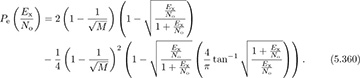
A comparison of both the exact and upper bounds is provided in Figure 5.36 for 4-QAM. Here it is apparent that the upper bound is loose but has the correct slope at high SNR.
){kind=link}
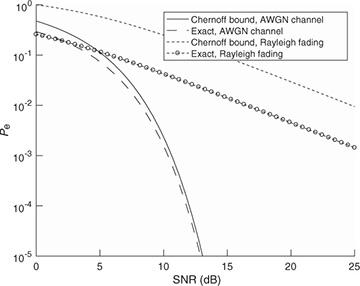
Figure 5.36 Probability of error curve comparing Gaussian and Rayleigh fading for 4-QAM
The implication of (5.358) is that the probability of error decreases as a function of the inverse of the SNR for Rayleigh fading channels. Note, though, that for the non-fading AWGN channel, the probability of error decreases exponentially (this can be visualized from the Chernoff upper bound). This means that fading channels require a much higher average SNR to achieve a given probability of error. The difference between the required SNR for an AWGN channel at a particular error rate and the target required for a fading channel is known as the small-scale fading margin. This is the extra power required to compensate for fading in the channel. An illustration is provided in Figure 5.36 for 4-QAM. For example, at a symbol error rate of 10−2, 4dB of SNR are required for an AWGN channel but 14dB are required for the Rayleigh channel. This means that a 10dB small-scale fade margin would be required in Rayleigh fading compared to an AWGN channel.