- 5.1 Frequency-Flat Wireless Channels
- 5.2 Equalization of Frequency-Selective Channels
- 5.3 Estimating Frequency-Selective Channels
- 5.4 Carrier Frequency Offset Correction in Frequency-Selective Channels
- 5.5 Introduction to Wireless Propagation
- 5.6 Large-Scale Channel Models
- 5.7 Small-Scale Fading Selectivity
- 5.8 Small-Scale Channel Models
- 5.9 Summary
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
5.5 Introduction to Wireless Propagation
Of all the impairments, the propagation channel has the most impact on the design of a wireless receiver. The wireless channel causes the transmitted signal to lose power as it propagates from the transmitter to the receiver. Reflections, diffraction, and scattering create multiple propagation paths between the transmitter and the receiver, each with a different delay. The net result is that wireless propagation leads to a loss of received signal power as well as the presence of multipath, which creates frequency selectivity in the channel. In this section, we provide an introduction to the key mechanisms of propagation. Then we rationalize the need for developing models and explain the distinction between large-scale models (discussed further in Section 5.6) and small-scale models (discussed further in Section 5.7 and Section 5.8). In this section, we briefly describe important factors affecting propagation in wireless channels to explain the need for several different channel models. The interested reader is referred to [270] or [165] for more extensive treatment of wireless propagation.
5.5.1 Mechanisms of Propagation
In a wireless communication system, a transmitted signal can reach the receiver via a number of propagation mechanisms. In this section, we review at a high level these key mechanisms, each potentially associated with a different propagation path. These mechanisms are illustrated in Figure 5.30.
){kind=link}
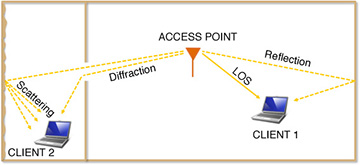
Figure 5.30 The mechanisms of propagation in the context of an indoor wireless local area network. The LOS path is unobstructed between the access point and client 1. That client also receives weaker signals as a result of a reflection off of a wall. The LOS path is obstructed for client 2, who instead receives signals through diffraction in the doorway and also scattering off of a rough wall.
When a signal reaches the receiver from the transmitter in a single path, without suffering any reflections, diffractions, or scattering, this is known as propagation along the line-of-sight (LOS) path. An LOS component has the shortest time delay among all the received signals and is usually the strongest signal received. The exact classification of a path being LOS requires that any obstructions be sufficiently far away from the path, which is quantified by the idea of the Fresnel zone [270].
In non-line-of-sight (NLOS) propagation, a signal transmitted into a wireless medium reaches the receiver via one or more indirect paths, each having different attenuations and delays. When a transmitted signal travels through communication paths other than the LOS path to reach the receiver, it is said to have undergone NLOS propagation. NLOS propagation is responsible for coverage behind buildings and other obstructions. The main NLOS propagation mechanisms are reflection, scattering, and diffraction.
Reflection occurs when a wave impinges on an object that is smooth, which means that any protrusions have dimensions much larger than a wavelength. Reflection is accompanied by refraction (transmission of the wave through the object). The strengths of the reflected and refracted waves depend on the type of material. The angles and indices of reflection and refraction are given by Snell’s law.
Scattering is what happens when a wave impinges on an object that is rough or has irregularities with dimensions on the order of the wavelength. It is similar to reflection but results in a smearing of the signal around the angle of reflection. This leads to a larger loss of energy as the signal is spread over a wider area. It also results in multiple paths arriving at the receiver from a similar location with slight differences in delay.
Diffraction is the “bending” of waves around sharp corners. Important examples of diffraction include waves bending over the tops of buildings, around street corners, and through doorways. Diffraction is one of the main ways that it is possible to provide cellular coverage in cities and is one reason why lower frequencies, say less than 3GHz, are considered beachfront property in the world of cellular spectrum.
There are other mechanisms of propagation as well, such as tropospheric or ionospheric scattering, but these are not common in land mobile systems. They do have relevance, though, for battlefield networks and for amateur radio enthusiasts.
5.5.2 Propagation Modeling
Propagation has an impact on several aspects of radio link performance. It determines the received signal strength and thus the signal-to-noise ratio, throughput, and probability of error. Propagation also plays a major role in system design and implementation. For example, it determines the length of the discrete-time channel, which determines how much equalization is required and in turn how much training is required. The speed at which the channel varies determines the frequency of equalization and the frequency of training—in other words, how often the channel must be reestimated.
An important component of the study of wireless communication is propagation modeling. A propagation model is a mathematical model (typically stochastic) to characterize either the propagation channel or some function of the propagation channel. Some models try to model the impulse response of the channel, whereas others try to model specific characteristics of the channel like the received power. Propagation models are usually inspired by measurement campaigns. Some models have many parameters and are designed to model specified real-world propagation scenarios. Other models have few parameters and are more amenable for tractable mathematical analysis.
There are many ways to classify propagation models. A common first-order classification is whether they describe large-scale or small-scale phenomena. The term scale refers to a wavelength. Large-scale phenomena refer to propagation characteristics over hundreds of wavelengths. Small-scale phenomena refer to propagation characteristics in an area on the order of a wavelength.
To illustrate different large-scale and small-scale phenomena, consider the average received signal power as a function of distance in Figure 5.31. Three different received signal power realizations are plotted. The first model is the mean (or median) path loss, which characterizes the average signal behavior, where the average is taken over hundreds of wavelengths. In most models, this is an exponential decay with distance. The second model is path loss with shadow fading. Here large obstructions like buildings or foliage are included to provide variability around the mean on a large scale. Shadow fading is often modeled by adding a Gaussian random component (in decibels) parameterized by the standard deviation to the mean path loss. The third model also includes small-scale fading, where the signal level experiences many small fluctuations as a result of the constructive and destructive addition of the multipath components of a transmitted signal. Because the fluctuations happen over a much smaller spatial scale, it is common to develop separate models for large-scale effects (like mean path loss and shadowing) and small-scale effects (like multipath fading).
){kind=link}
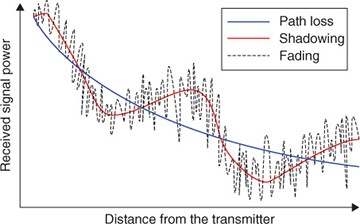
Figure 5.31 Representation of the large-scale (distance-dependent path loss and shadowing) and small-scale (fading) propagation effects
In essence, large-scale fading models describe the average behavior of the channel in a small area and are used to infer channel behavior over longer distances. Small-scale fading models describe the localized fluctuations in a given area and may be location dependent.
Models for both large-scale and small-scale propagation phenomena are important. Large-scale trends influence system planning, the link budget, and network capacity predictions, and they capture the “typical” loss in received signal strength as a function of distance. Small-scale trends influence physical-layer link design, modulation schemes, and equalization strategies by capturing local constructive and destructive multipath effects. The received signal processing algorithms depend more strongly on small-scale models, but the net performance of those algorithms in a system depends on the large-scale models as well.
Propagation models are widely used for wireless system design, evaluation, and algorithm comparison. Standards bodies (IEEE 802.11, 3GPP, etc.) find them useful for enabling different companies to compare and contrast performance of different candidate schemes. Often these models are chosen to suit certain characteristics like propagation environment (urban, rural, suburban) or receiver speed (fixed, pedestrian, or high speed). The models typically have many possible parameter choices and are used primarily as part of system simulation.
In this section, we focus on developing models for the discrete-time equivalent channel. We decompose the channel taps as a product of a large-scale coefficient and a small-scale coefficient as
The large-scale gain is G = Ex/Prx,lin(d) where Prx,lin(d) is the distance-dependent path-loss term in linear (to distinguish it from the more common decibel measure Prx(d)). The small-scale fading coefficient is denoted by hs[ℓ]. The path loss is the ratio of the transmit power to the receive power and is often called the path gain for this reason. With complex pulse-amplitude modulation, for example, the transmit power is Ex/T, so the received power is (Ex/T)/Prx,lin(d). In Section 5.6, we describe models for Prx(d), including free space, log distance, and shadowing. In Section 5.8, we describe models for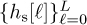 
, some that are good for analysis like the IID Rayleigh fading model, and others that are inspired by physical mechanisms of propagation like the clustered model.