Dealing with Impairments in Wireless Communication

This chapter is from the book

Introduction to Wireless Digital Communication: A Signal Processing Perspective

Learn More Buy

This chapter is from the book

This chapter is from the book 

Introduction to Wireless Digital Communication: A Signal Processing Perspective

Learn More Buy

5.4 Carrier Frequency Offset Correction in Frequency-Selective Channels

In this section, we describe the carrier frequency offset impairment for frequency-selective channels. We present a discrete-time received signal model that includes frequency offset. Then we examine several carrier frequency offset estimation algorithms. We also remark how each facilitates frame synchronization.

5.4.1 Model for Frequency Offset in Frequency-Selective Channels

In Section 5.1.6, we introduced the carrier frequency offset problem. In brief, carrier frequency offset occurs when the carrier used for upconversion and the carrier used for downconversion are different. Even a small difference can create a significant distortion in the received signal.

We have all the ingredients to develop a signal model for frequency offset in frequency-selective channels. Our starting point is to recall (5.67), which essentially says that carrier frequency offset multiplies the matched filtered received signal by e^j2πf_et. Sampling at the symbol rate, and using our FIR model for the received signal in (5.87), we obtain

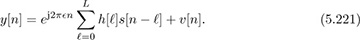
It is possible to further generalize (5.221) to include frame synchronization by including a delay of d. Correction of carrier frequency offset therefore amounts to estimating 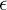and then derotating the received signals e^−j2π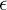ny[n].

In the frequency-flat case, the frequency offset creates a successive rotation of each symbol by exp(j2π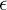n). In the frequency-selective case, this rotation is applied to the convolutive mixture between the symbols and the channel. As a result, the carrier frequency offset distorts the data that would otherwise be used for channel estimation and equalization. Even if training data is available, it does not lead directly to a simple estimator. A direct extension of what we have studied leads to a joint carrier frequency offset and channel estimation problem, which has high complexity. In this section, we review several lower-complexity methods for frequency offset estimation, which rely on special signal structure to implement.

5.4.2 Revisiting Single-Frequency Estimation

For our first estimator, we revisit the estimator proposed in Example 5.8 and show how it can also be used in frequency-selective channels with minimal changes. This type of sinusoidal training was used in the GSM system through a special input to the GMSK (Gaussian minimum shift keying) modulator.

Let us choose as a training sequence t[n] = exp(j2πf_tn) for n = 0, 1, . . . , N_tr − 1 where f_t is a discrete-time design frequency. Consider the received signal (5.87) with s[n] = t[n] for n = 0, 1, . . . , N_tr − 1. Discarding samples that do not depend on the training, we have the received signal

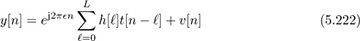
for n = L, L + 1, . . . , N_tr − 1. Substituting for the training signal,

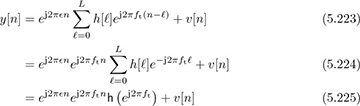
where h (e^j2πf_t) is the DTFT of h[n]. Derotating by the known frequency of the training signal,

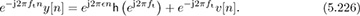
This has the form of (5.72) from Example 5.8. As a result, the estimators for frequency-flat frequency offset estimation using sinusoidal training can also be applied to the frequency-selective case.

The main signal processing trick in deriving this estimator was to recognize that signals of the form exp(j2πf_tn) are eigenfunctions of discrete-time LTI systems. Because the unknown channel is FIR with order L, and the training N_tr > L, we can discard some samples to remove the edge effects. The frequency f_t could be selected of the form k/N_tr to take advantage, for example, of subsequent frequency-domain processing in the modem.

The main advantage of single-frequency estimation is that any number of good algorithms can be used for estimation; see, for example, [330, 3, 109, 174, 212, 218] among others. The disadvantage of this approach is that performance is limited by h (e^j2πf_t). Since the channel is frequency selective by assumption and has L zeros because it is FIR of order L, it could happen that the chosen frequency of f_t is close to a zero of the channel. Then the SNR for the estimator would be poor. The sinusoidal training also does not lead to a sharp correlation peak that can be used for frame detection. Furthermore, if used to construct T in (5.175), it would in fact not have full rank, and thus it could not be used for channel estimation. As a result, we now review other approaches for carrier frequency offset estimation.

5.4.3 Frequency Offset Estimation and Frame Synchronization Using Periodic Training for Single-Carrier Systems

There are several different algorithms for frequency offset estimation using different properties of the transmitted signal such as periodicity, constant modulus, and so on. One of the most elegant methods was proposed by Moose [231] and has since been studied extensively. This method relies on a special periodic training sequence that permits joint carrier frequency offset estimation and frame synchronization. The training sequences can also be used for channel estimation. Periodic training has found application in IEEE 802.11a/g/n/ac systems and others. In this section, we consider the application of periodic training to a single-carrier system, though note that Moose’s original application was to OFDM. We deal with the case of OFDM, including another algorithm called the Schmidl-Cox approach [296], in the next section.

Now we explain the key idea behind the Moose algorithm from the perspective of using just two repeated training sequences. Other extensions are possible with multiple repetitions. Consider the framing structure illustrated in Figure 5.27. In this frame, a pair of training sequences are sent together, followed by a data sequence.

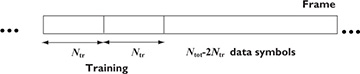
Figure 5.27 The framing used in the Moose estimator. A pair of training sequences are followed by data.

The Moose algorithm exploits the periodicity in the training sequence. Let the training sequence start at n = 0. Then

for n = 0, 1, . . . , N_tr − 1. Note that symbols s[n] for n < 0 and n ≥ 2N_tr are unknown (they are either zero or correspond to the unknown portions of the data).

Now we explain the trick associated with periodicity in the training data. For n ∈ [L, N_tr − 1],

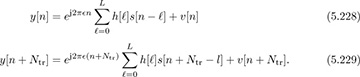
Using the fact that s[n + N_tr] = s[n] = t[n] for n = 0, 1, . . . , N_tr − 1:

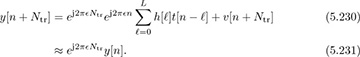
To see the significance of this result, remember that the channel coefficients 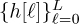are unknown! The beauty of (5.231) is that it is a function of known observations and only the unknown frequency offset. Essentially, the periodicity establishes a relationship between different parts of the received signal y[n]. This is an amazing observation, since it does not require any assumptions about the channel.

There are several possible approaches for solving (5.231). Note that this is slightly different from the single-frequency estimator because of the presence of y[n] on the right-hand side of (5.231). The direct least squares approach is not possible since the unknown parameter is present in the exponent of the exponential. A solution is to consider a relaxed problem

solving for 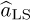and then finding 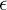from the phase. This problem is similar to flat-fading channel estimation in Section 5.1.4. Using (5.47), we can write

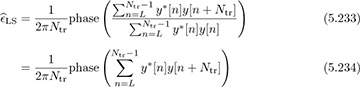
where we can neglect the denominator since it does not contribute to the phase estimate. Despite the relaxation in this derivation, it turns out that this is also the maximum likelihood estimator [231].

There is an important limitation in the Moose algorithm. Because of the periodicity of discrete-time exponentials, the estimate of 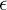is accurate only for 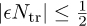or equivalently

which in terms of the actual frequency offset means

This reveals an interesting trade-off in the estimator performance. Choosing larger N_tr improves the estimate since there is more noise averaging, but it reduces the range of offsets that can be corrected. A way of solving this problem is to use multiple repetitions of a short training sequence. IEEE 802.11a and related standards use a combination of both repeated short training sequences and long training sequences.

Example 5.19 Compute the maximum allowable offset for a 1Ms/s-QAM signal, with f_c = 2GHz and N_t = 10.

Answer:

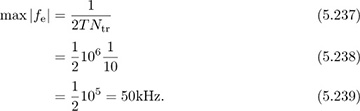
In terms of parts per million, we need an oscillator that can generate a 2GHz carrier with an accuracy of 50e3/2e9 = 25ppm.

Example 5.20 Consider a wireless system where each data frame is preceded by two training blocks, each consisting of N_tr = 12 training symbols. Let the symbol period be T = 4µs. What is the maximum frequency offset that can be corrected using training?

Answer: The maximum frequency offset that can be corrected using training is 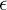= 1/(2N_tr) ≈ 0.0417 or f_e = 1/(2TN_tr) ≈ 10.417kHz.

The Moose algorithm also provides a nice way of performing frame synchronization. The observation is that the correlation peak should occur when the pair of training sequences is encountered at the receiver. Essentially, this involves solving for the offset d such that

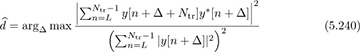
where the search is performed over a reasonable set of possible values of d. For example, the analog RF may perform carrier sensing, activating the ADCs only when a sufficiently strong signal is present.

The denominator normalization in the frame synchronization is required to avoid false positives when there is no signal present. An alternative solution, which is somewhat more robust in this case, involves normalizing by both observed vectors as in

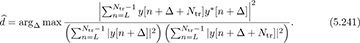
No matter which algorithm is used, both result in the same thing: a joint solution to the frame synchronization and frequency offset estimation and correction problem in an intersymbol interference channel.

Channel estimation is also facilitated using the Moose algorithm. Once the frequency offset is estimated and corrected, and the frame is synchronized, the pair of training sequences can be combined for channel estimation. As a result, periodic training provides a flexible approach for solving key receiver functions in frequency-selective channels.

An illustration of the complete receiver can be found in Figure 5.28. The frequency offset estimation and correction are performed prior to channel estimation and equalization but after the downsampling operation. Better performance could be achieved by operating before the downsampling, replacing the symbol synchronizer, but this is usually practical only for smaller values of M_rx.

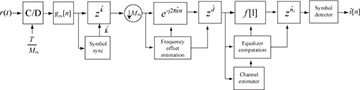
Figure 5.28 A single-carrier receiver with frequency offset estimation and correction, frame synchronization, channel estimation, and linear equalization. The linear equalization could be replaced by an SC-FDE receiver structure with no other changes required.

We conclude this section with a detailed example that describes how to use the preamble structure in IEEE 802.15.3c single-carrier mode and in IEEE 802.11a.

Example 5.21 Consider the IEEE 802.15.3c preamble structure as described in Example 5.17 for the high-rate mode of the SC-PHY. In this example, we describe how the SYNC field is used for carrier frequency offset estimation and frame synchronization. Note that the standard just describes the preamble itself; it does not describe how the receiver signal processing should be applied to the preamble. A good description of digital synchronization algorithms for IEEE 802.15.3c is found in [204].

The SYNC field can be used for frame synchronization and carrier frequency offset estimation. The SYNC field contains 14 repetitions of a₁₂₈. Because the maximum supported channel length is L_c = 128, though, the first repetition acts as a cyclic prefix. Therefore, we can use the following frame detection algorithm:

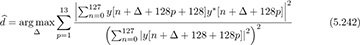
where we have put the packet energy in the denominator to make the algorithm more robust when averaging over multiple repetitions. The carrier frequency offset can then be estimated from either averaging the offset with each period and combining or taking the phase of the average as

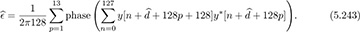
The maximum absolute offset correctable is 1/256.

In packet-based wireless systems, the digital part of the receiver may be in sleep mode to save power. As a result, the analog may make an initial determination that there is a signal of interest, for example, if the signal exceeds a threshold. The SYNC field can be used for this initial determination. In the process, though, some samples may be lost, and not all repetitions will be available for averaging. As a result, it may make sense to average over fewer repetitions in (5.242). It also may make sense to either defer frequency offset correction or make a correction based on this tentative estimate (called a coarse correction), then proceed with further correction and refinement using the SFD field.

Example 5.22 Consider the IEEE 802.11a preamble structure as described in Example 5.18. In this example, we explain the coarse frequency offset using the STF field and the fine frequency offset using the CEF field. We assume B = 20MHz bandwidth. The STF field (in the time domain) consists of ten repetitions (created by zeroing subcarriers as described in Section 5.4.4). The CEF field has two repetitions. Sampled at T = 1/B, each repetition of the STF contains 16 samples, whereas the CEF has two repetitions of 64 samples with a length 32 cyclic prefix.

The STF field is used for functions such as packet detection, automatic gain control (AGC), and coarse synchronization. Because the RF may be powering up, and the AGC adjusting, not all of the ten repetitions are typically used for synchronization. For example, suppose that three repetitions are used with the first acting as a cyclic prefix. Then we use the following frame detection algorithm:

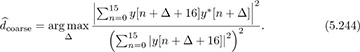
The coarse carrier frequency offset estimate is then

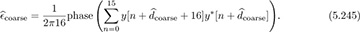
The maximum absolute frequency offset correctable is 1/32.

Next, we correct for the coarse frequency offset to create the new signal 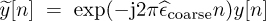. Using this corrected signal, we then search for the long training sequence:

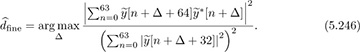
The coarse frame synchronization estimate can be used to reduce the search space of possible offsets. The fine carrier frequency offset estimate is then

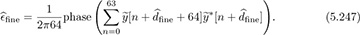
The two-step approach allows an initial frequency offset estimate with a larger correction range, but it is noisier in the first step because of the use of only 16 samples. Then, in the second step, it is possible to get a more accurate estimate by using 64 samples with a smaller range, assuming the first phase corrected for the larger errors.

5.4.4 Frequency Offset Estimation and Frame Synchronization Using Periodic Training for OFDM Systems

OFDM is sensitive to carrier frequency offset. The reason is essentially that carrier frequency offset over the duration of an OFDM symbol creates problems because the DFT is taken over the whole OFDM symbol period. Small variations are compounded by the DFT operation into bigger variations.

Frequency offset correction algorithms for OFDM systems are similar to their time-domain counterparts. The method in Section 5.4.2 can be applied to OFDM by sending a OFDM symbol with just a single subcarrier active. The method in Section 5.4.3 can be applied directly only to multiple repetitions of OFDM systems. In this section, we develop another carrier frequency offset estimator that works on the periodicity created in one OFDM symbol. It also has an advantage over the Moose method in that it allows a larger range of offsets to be corrected, when used with a second specially designed OFDM symbol.

We start by explaining how to create periodicity in a single OFDM symbol. The key insight is to make a portion of the transmitted signal look periodic and then to apply the same technique as before. Suppose that we construct an OFDM symbol where all the odd subcarriers are zero. Then

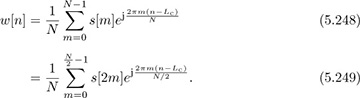
This looks like an extended discrete-time sinusoid with carrier 2π(N/2). As a result, for n ∈ [L_c, L_c + N/2],

which means that the OFDM signal contains a portion that is periodic. As a result, the Moose algorithm can be applied directly to this setting.

Consider the case where frame synchronization has already been performed. The received signal model is

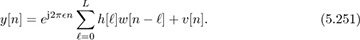
Discarding the cyclic prefix,

Because of the periodicity,

Then the Moose frequency offset estimator is

As before, it is possible to perform OFDM symbol synchronization (or frame synchronization) and frequency offset estimation jointly using this correlation method. The OFDM training symbol can even be used for channel estimation as this is just a special case of the comb-type pilot arrangement described in Section 5.3.2.

The maximum correctable carrier frequency offset is

As a result, the Moose algorithm can essentially correct for continuous-time offsets that are less than one subcarrier spacing 1/(NT). In an OFDM system, N may be quite large. This would in turn reduce the range of correctable offsets. Thus, it is of interest to develop techniques to enhance the range. One such approach is the Schmidl-Cox algorithm [296].

Consider an OFDM system with two training OFDM symbols. In the first symbol, all the odd subcarriers are zero. The even subcarriers 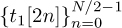are 4-QAM training symbols, which are nominally just a pseudo-noise sequence. The presence of zeros ensures that there is periodicity in the first OFDM symbol. Let 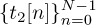be a set of 4-QAM training symbols sent on the second OFDM symbol, without zeros. Further suppose that the even training symbols are selected such that 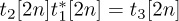where 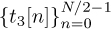is another sequence with good periodic correlation properties. Effectively, the training data on even subcarriers of the second OFDM symbol is differentially encoded.

The Schmidl-Cox algorithm works as follows. Let the frequency offset be written as

where q is called the integer offset and 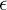_frac is the fractional offset. Because

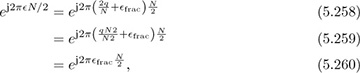
the expression (5.253) is able to account for only fractional frequency offsets. Suppose that the estimator in (5.254) is used to estimate the fractional frequency offset. Further suppose that the estimate is perfect and is then removed by multiplying by exp(−j2π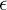_fracN/2), leaving the received signal after correction as

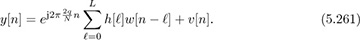
Discarding the cyclic prefix and taking the DFT gives

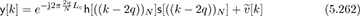
for k = 0, 1, . . . , N − 1. The received signals corresponding to each training symbol use the index k = 0, 1, . . . , N − 1:

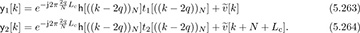
Now we exploit the fact that the training on the even subcarriers was differentially encoded. Consider

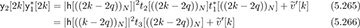
where 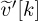contains the products with the noise terms. Because 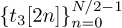has good periodic correlation properties, a least-squares-type problem can be formulated and used to find the shift with a correlation peak:

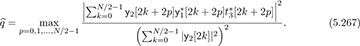
Based on this integer offset estimate, the received samples can be corrected by 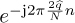. Then the second OFDM training symbol can be used to estimate the channel (possibly combined with the first OFDM symbol as well).

The final frequency offset estimate obtained with the Schmidl-Cox algorithm is

When both fractional and integer offset corrections are applied, a large range of offsets can be corrected. While it seems like very large offsets can be corrected, recall that the system model was derived assuming a small offset. A large offset would shift part of the desired signal outside the baseband lowpass filter, rendering the signal models inaccurate. In practice, this approach should be able to correct for offsets corresponding to several subcarriers, depending on the analog filtering, digital filtering, and extent over oversampling.

Like the Moose method, the Schmidl-Cox approach can also be used for OFDM symbol synchronization, by looking for a correlation peak around the first OFDM symbol as

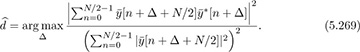
There is one distinct point of difference, though. With OFDM, there is also a cyclic prefix and often L_c > L. In this case, then

for n = L, L + 1, . . . , L_c, L_c + 1, . . . , N + L_c − 1. This means that there will be some ambiguity in (5.269), in that there may be several values of d that are close, especially when L_c is much larger than L. This creates a plateau in the symbol synchronization algorithm [296]. Any value within the plataeu, however, should give acceptable performance if the estimated channel has order L_c, but if the smaller channel length of L is assumed, then performance may suffer. Other training sequence designs can improve the sharpness of the frame synchronization, specifically with multiple repetitions along with a sign change among the different repetitions [306].

A system block diagram with OFDM and frame synchronization, channel estimation, and carrier frequency offset correction is illustrated in Figure 5.29. One frequency offset correction block is shown, but this could be broken up into two pieces corresponding to integer and fine offsets.

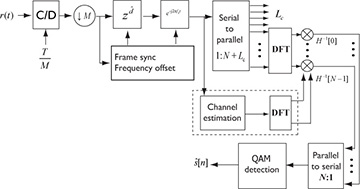
Figure 5.29 OFDM receiver frequency offset estimation and correction, channel estimation, and linear equalization. The matched filtering and symbol sampling are omitted as they are often not performed in OFDM.

Example 5.23 In this example, we show how the STF in IEEE 802.11a is constructed to have periodicity. The STF is generated from a special training sequence with 12 nonzero values constructed as

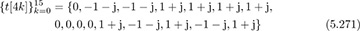
for k = 0, 1, . . . , 15 and the other undefined values of the training are zero.

The presence of zeros in (5.271) is a result of the need for eliminating the DC subcarrier and spectral shaping, similar to the design of the CEF. Based on this training sequence,

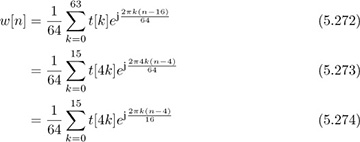
for n = 0, 1, . . . , 159. The time-domain waveform thus contains ten repetitions of length 16.