- 1.1 Fluid Mechanics in Chemical Engineering
- 1.2 General Concepts of a Fluid
- 1.3 Stresses, Pressure, Velocity, and the Basic Laws
- 1.4 Physical Properties-Density, Viscosity, and Surface Tension
- 1.5 Units and Systems of Units
- 1.6 Hydrostatics
- 1.7 Pressure Change Caused by Rotation
- Problems for Chapter 1
This chapter is from the book
This chapter is from the book
This chapter is from the book
Problems for Chapter 1
Units conversion—E. How many cubic feet are there in an acre-foot? How many gallons? How many cubic meters? How many tonnes of water?
Units conversion—E. The viscosity μ of an oil is 10 cP, and its specific gravity s is 0.8. Reexpress both of these (the latter as density ρ) in both the lbm, ft, s system and in SI units.
Units conversion—E. Use conversion factors to express: (a) the gravitational acceleration of 32.174 ft/s2 in SI units, and (b) a pressure of 14.7 lbf/in2 (one atmosphere) in both pascals and bars.
Meteorite density—E. The Barringer Crater in Arizona was formed 30,000 years ago by a spherical meteorite of diameter 60 m and mass 106 t (tonnes), traveling at 15 km/s when it hit the ground.9 (Clearly, all figures are estimates.) What was the mean density of the meteorite? What was the predominant material in the meteorite? Why? If one tonne of the explosive TNT is equivalent to five billion joules, how many tonnes of TNT would have had the same impact as the meteorite?
Reynolds number—E. What is the mean velocity um (ft/s) and the Reynolds number Re = ρumD/μ for 35 gpm (gallons per minute) of water flowing in a 1.05-in. I.D. pipe if its density is ρ = 62.3 lbm/ft3 and its viscosity is μ = 1.2 cP? What are the units of the Reynolds number?
Pressure in bubble—E. Consider a soap-film bubble of diameter d. If the external air pressure is pa, and the surface tension of the soap film is σ, derive an expression for the pressure pb inside the bubble. Hint: Note that there are two air/liquid interfaces.
Reservoir waterflooding—E. Fig. P1.7(a) shows how water is pumped down one well, of depth H, into an oil-bearing stratum, so that the displaced oil then flows up through another well. Fig. P1.7(b) shows an enlargement of an idealized pore, of diameter d, at the water/oil interface.
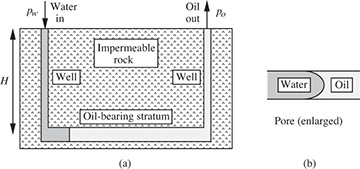
Fig. P1.7 Waterflooding of an oil reservoir.
If the water and oil are just starting to move, what water inlet pressure pw is needed if the oil exit pressure is to be po? Assume that the oil completely wets the pore (not always the case), that the water/oil interfacial tension is σ, and that the densities of the water and oil are ρw and ρo, respectively.10
Barometer reading—M. In your house (elevation 950 ft above sea level) you have a barometer that registers inches of mercury. On an average day in January, you telephone the weather station (elevation 700 ft) and are told that the exact pressure there is 0.966 bar. What is the correct reading for your barometer, and to how many psia does this correspond? The specific gravity of mercury is 13.57.
Two-layer buoyancy—E. As shown in Fig. P1.9, a layer of an unknown liquid A (immiscible with water) floats on top of a layer of water W in a beaker. A completely submerged cylinder of specific gravity 0.9 adjusts itself so that its axis is vertical and two-thirds of its height projects above the A/W interface and one-third remains below. What is the specific gravity of A? Solve the problem two ways—first using Archimedes’ law and then using a momentum or force balance.
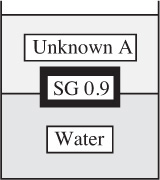
Fig. P1.9 Cylinder immersed in water and liquid A.
Differential manometer—E. The U-tube shown in Fig. P1.10 has legs of unequal internal diameters d1 and d2, which are partly filled with immiscible liquids of densities ρ1 and ρ2, respectively, and are open to the atmosphere at the top.
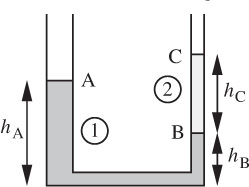
Fig. P1.10 U-tube with immiscible liquids.
If an additional small volume v2 of the second liquid is added to the right-hand leg, derive an expression—in terms of ρ1, ρ2, v2, d1, and d2—for δ, the amount by which the level at B will fall. If ρ1 is known, but ρ2 is unknown, could the apparatus be used for determining the density of the second liquid?
Hints: The lengths hA, hB, and hC have been included just to get started; they must not appear in the final result. After adding the second liquid, consider hC to have increased by a length Δ—a quantity that must also eventually be eliminated.
Ascending bubble—E. As shown in Fig. P1.11, a hollow vertical cylinder with rigid walls and of height H is closed at both ends and is filled with an incompressible oil of density ρ. A gauge registers the pressure at the top of the cylinder. When a small bubble of volume v0 initially adheres to point A at the bottom of the cylinder, the gauge registers a pressure p0. The gas in the bubble is ideal and has a molecular weight of Mw. The bubble is liberated by tapping on the cylinder and rises to point B at the top. The temperature T is constant throughout. Derive an expression in terms of any or all of the specified variables for the new pressure-gauge reading p1 at the top of the cylinder.
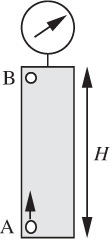
Fig. P1.11 Bubble rising in a closed cylinder.
Ship passing through locks—M. A ship of mass M travels uphill through a series of identical rectangular locks, each of equal superficial (bird’s-eye view) area A and elevation change h. The steps involved in moving from one lock to the next (1 to 2, for example) are shown as A–B–C in Fig. P1.12. The lock at the top of the hill is supplied by a source of water. The initial depth in lock 1 is H, and the density of the water is ρ.
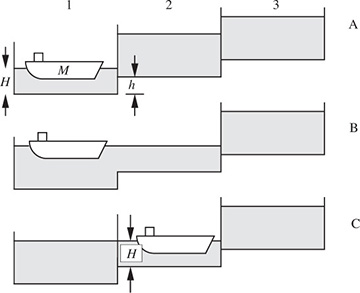
Fig. P1.12 Ship and locks.
Derive an expression for the increase in mass of water in lock 1 for the sequence shown in terms of some or all of the variables M, H, h, A, ρ, and g.
If, after reaching the top of the hill, the ship descends through a similar series of locks to its original elevation, again derive an expression for the mass of water gained by a lock from the lock immediately above it.
Does the mass of water to be supplied depend on the mass of the ship if: (i) it travels only uphill, (ii) it travels uphill, then downhill? Explain your answer.
Furnace stack—E. Air (ρa = 0.08 lbm/ft3) flows through a furnace where it is burned with fuel to produce a hot gas (ρg = 0.05 lbm/ft3) that flows up the stack, as in Fig. P1.13. The pressures in the gas and the immediately surrounding air at the top of the stack at point A are equal.
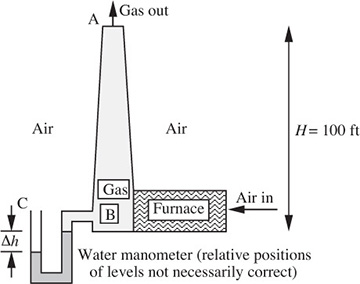
Fig. P1.13 Furnace stack.
What is the difference Δh (in.) in levels of the water in the manometer connected between the base B of the stack and the outside air at point C? Which side rises? Except for the pressure drop across the furnace (which you need not worry about), treat the problem as one in hydrostatics. That is, ignore any frictional effects and kinetic energy changes in the stack. Also, neglect compressibility effects.
Hydrometer—E. When a hydrometer floats in water, its cylindrical stem is submerged so that a certain point X on the stem is level with the free surface of the water, as shown in Fig. P1.14. When the hydrometer is placed in another liquid L of specific gravity s, the stem rises so that point X is now a height z above the free surface of L.
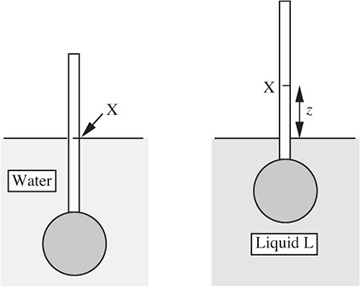
Fig. P1.14 Hydrometer in water and test liquid L.
Derive an equation giving s in terms of z. If needed, the cross-sectional area of the stem is A, and when in water a total volume V (stem plus bulb) is submerged.
Three-liquid manometer—E. In the hydrostatic case shown in Fig. P1.15, a = 6 ft and c = 4 ft. The specific gravities of oil, mercury, and water are so = 0.8, sm = 13.6, and sw = 1.0. Pressure variations in the air are negligible. What is the difference b in inches between the mercury levels, and which leg of the manometer has the higher mercury level? Note: In this latter respect, the diagram may or may not be correct.
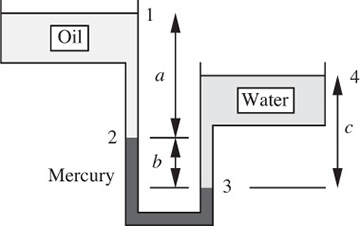
Fig. P1.15 Oil/mercury/water system.
Pressure on Mt. Erebus—M. On page 223 of the biography Shackleton (by Roland Huntford, Atheneum, New York, 1986), the Antarctic explorer’s colleague, Edward Marshall, is reported as having “fixed the altitude [of Mt. Erebus] by hypsometer. This was simply a small cylinder in which distilled water was boiled and the temperature measured. It was then the most accurate known method of measuring altitude. The summit of Erebus turned out to be 13,500 feet above sea level.”11
Assuming a uniform (mean) air temperature of –5 °F (the summer summit temperature is –30 °F) and a sea-level pressure of 13.9 psia, at what temperature did the water boil in the hypsometer? At temperatures T = 160, 170, 180, 190, 200, and 210 °F, the respective vapor pressures of water are pv = 4.741, 5.992, 7.510, 9.339, 11.526, and 14.123 psia.
Oil and gas well pressures—M. A pressure gauge at the top of an oil well 18,000 ft deep registers 2,000 psig. The bottom 4,000-ft portion of the well is filled with oil (s = 0.70). The remainder of the well is filled with natural gas (T = 60 °F, compressibility factor Z = 0.80, and s = 0.65, meaning that the molecular weight is 0.65 times that of air).
Calculate the pressure (psig) at (a) the oil/gas interface, and (b) the bottom of the well.
Thrust on a dam—E. Concerning the thrust on a rectangular dam, check that Eqn. (1.36) is still obtained if, instead of employing an upward coordinate z, use is made of a downward coordinate h (with h = 0 at the free surface).
Pressure variations in air—M. Refer to Example 1.5 concerning the pressure variations in a gas, and assume that you are dealing with air at 40 °F. Suppose further that you are using just the linear part of the expansion (up to the term in z) to calculate the absolute pressure at an elevation z above ground level. How large can z be, in miles, with the knowledge that the error amounts to no more than 1% of the exact value?
Grand Coulee dam—E. The Grand Coulee dam, which first operated in 1941, is 550 ft high and 3,000 ft wide. What is the pressure at the base of the dam, and what is the total horizontal force F lbf exerted on it by the water upstream?
Force on V-shaped dam—M. A vertical dam has the shape of a V that is 3 m high and 2 m wide at the top, which is just level with the surface of the water upstream of the dam. Use two different methods to determine the total force (N) exerted by the water on the dam.
Rotating mercury mirror—M. Physicist Ermanno Borra, of Laval University in Quebec, has made a 40-in. diameter telescopic mirror from a pool of mercury that rotates at one revolution every six seconds.12 (Air bearings eliminate vibration, and a thin layer of oil prevents surface ripples.)
By what value Δz would the surface at the center be depressed relative to the perimeter, and what is the focal length (m) of the mirror? The mirror cost Borra $7,500. He estimated that a similar 30-meter mirror could be built for $7.5 million. If the focal length were unchanged, what would be the new value of Δz for the larger mirror? Hint: the equation for a parabola of focal length f is r2 = 4fz.
Oil and water in rotating container—E. A cylindrical container partly filled with immiscible layers of water and oil is placed on a rotating turntable. Develop the necessary equations and prove that the shapes of the oil/air and water/oil interfaces are identical.
Energy to place satellite in orbit—M. “NASA launched a $195 million astronomy satellite at the weekend to probe the enigmatic workings of neutron stars, black holes, and the hearts of galaxies at the edge of the universe . . . The long-awaited mission began at 8:48 a.m. last Saturday when the satellite’s Delta–2 rocket blasted off from the Cape Canaveral Air Station.”13
This “X-ray Timing Explorer satellite” was reported as having a mass of 6,700 lbm and being placed 78 minutes after lift-off into a 360-mile-high circular orbit (measured above the earth’s surface).
How much energy (J) went directly to the satellite to place it in orbit? What was the corresponding average power (kW)? The force of attraction between a mass m and the mass Me of the earth is GmMe/r2, where r is the distance of the mass from the center of the earth and G is the universal gravitational constant. The value of G is not needed in order to solve the problem, as long as you remember that the radius of the earth is 6.37 × 106 m and that g = 9.81 m/s2 at its surface.
Central-heating loop—M. Fig. P1.25 shows a piping “loop” that circulates hot water through the system ABCD in order to heat two floors of a house by means of baseboard fins attached to the horizontal runs of pipe (BC and DA). The horizontal and vertical portions of the pipes have lengths L and H, respectively.
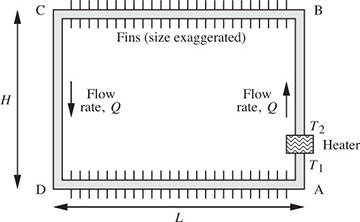
Fig. P1.25 Central-heating loop.
The water, which has a mean density of
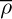and a volume coefficient of expansion α, circulates by the action of natural convection due to a small heater, whose inlet and outlet water temperatures are T1 and T2, respectively. The pressure drop due to friction per unit length of piping is cu2/D, where c is a known constant, u is the mean water velocity, and D is the internal diameter of the pipe. You may assume that the vertical legs AB and CD are insulated and that equal amounts of heat are dissipated on each floor.Derive an expression that gives the volumetric circulation rate of water, Q, in terms of c, D,
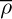, α, g, L, H, T1, and T2.Pressure at the center of the earth—M. Prove that the pressure at the center of the earth is given by pc = 3Mgs/8πR2, in which gs is the gravitational acceleration at the surface, M is the mass of the earth, and R is its radius. Hints: Consider a small mass m inside the earth, at a radius r from the center. The force of attraction mgr (where gr is the local gravitational acceleration) between m and the mass Mr enclosed within the radius r is GmMr/r2, where G is the universal gravitational constant. Repeat for the mass at the surface, and hence show that gr/gs = r/R. Then invoke hydrostatics.
If the radius of the earth is R = 6.37 × 106 m, and its mean density is approximately 5,500 kg/m3, estimate pc in Pa and psi.
Soap film on wire rings—M. As shown in Fig. P1.27, a soap film is stretched between two wire rings, each of diameter D and separated by a distance H. Prove that the radius R of the film at its narrowest point is:
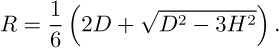
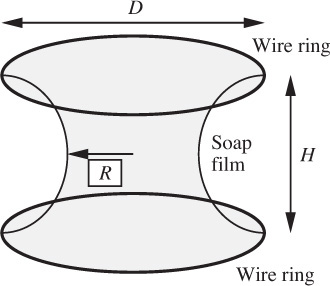
Fig. P1.27 Soap film on two rings.
You may assume that a section of the soap film is a circular arc and that
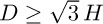. What might happen if D is less than 
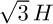?Clearly stating your assumptions, derive an expression for the radius, in terms of D and H. Is your expression exact or approximate? Explain.
Treadmill stress test—M. What power P is needed to resist a force F at a steady velocity V? In a treadmill stress test (Fig. P1.28), you have to keep walking to keep up with a moving belt whose velocity V and angle of inclination θ are steadily increased. Initially, the belt is moving at 1.7 mph and has a grade (defined as tan θ) of 10%. The test is concluded after 13.3 min, at which stage the belt is moving at 5.0 mph and has a grade of 18%. If your mass is 163 lbm: (a) how many HP are you exerting at the start of the test, (b) how many HP are you exerting at the end of the test, and (c) how many joules have you expended overall?
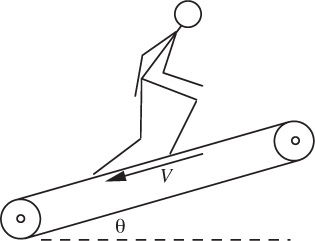
Fig. P1.28 Person on a treadmill.
Bubble rising in compressible liquid—D. A liquid of volume V and isothermal compressibility β has its pressure increased by an amount Δp. Explain why the corresponding increase ΔV in volume is given approximately by:
ΔV = –βV Δp.
Repeat Problem 1.11, now allowing the oil—whose density and volume are initially ρ0 and V0—to have a finite compressibility β. Prove that the ratio of the final bubble volume v1 to its initial volume v0 is:
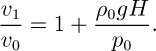
If needed, assume that: (a) the bubble volume is much smaller than the oil volume, and (b) βp0V0 ≫ v1. If ρ0 = 800 kg/m3, β = 5.5 × 10−10 m2/N, H = 1 m, p0 = 105 N/m2 (initial absolute pressure at the top of the cylinder), v0 = 10−8 m3, and V0 = 0.1 m3, evaluate v1/v0 and check that assumption (b) above is reasonable.
Pressures in oil and gas well—M. Fig. P1.30 shows a well that is 12,000 ft deep. The bottom H = 2, 000-ft portion is filled with an incompressible oil of specific gravity s = 0.75, above which there is an h = 10, 000-ft layer of methane (CH4; C = 12, H = 1) at 100 °F, which behaves as an ideal isothermal gas whose density is not constant. The gas and oil are static. The density of water is 62.3 lbm/ft3.
If the pressure gauge at the top of the well registers pA = 1, 000 psig, compute the absolute pressure pB (psia) at the oil/methane interface. Work in terms of symbols before substituting numbers.
Also compute (pC – pB), the additional pressure (psi) in going from the interface B to the bottom of the well C.
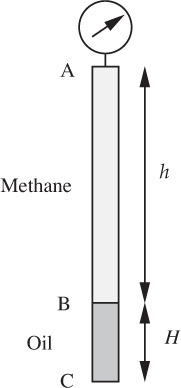
Fig. P1.30 Well containing oil and methane.
Soap film between disks—E (C). A circular disk of weight W and radius a is hung from a similar disk by a soap film with surface tension σ, as shown in Fig. P1.31. The gauge pressure inside the film is P.
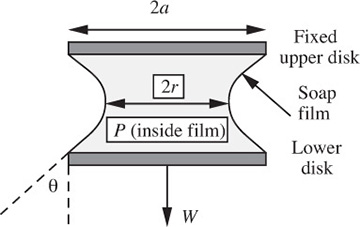
Fig. P1.31 Soap film between two disks.
First, derive an expression for the angle θ in terms of a, P, W, and σ. Then obtain an equation that relates the radius of the neck r to a, P, W, and σ. Assume that: (a) the excess pressure inside a soap film with radii of curvature r1 and r2 is 2σ(1/r1 + 1/r2), and (b) the cross section of the film forms a circular arc.
Newspaper statements about the erg—E. In the New York Times for January 18, 1994, the following statement appeared: “An erg is the metric unit scientists use to measure energy. One erg is the amount of energy it takes to move a mass of one gram one centimeter in one second.” (This statement related to the earthquake of the previous day, measuring 6.6 on the Richter scale, in the Northridge area of the San Fernando Valley, 20 miles north of downtown Los Angeles.)
Also in the same newspaper, there was a letter of rebuttal on January 30 that stated in part: “This is not correct. The energy required to move a mass through a distance does not depend on how long it takes to accomplish the movement. Thus the definition should not include a unit of time.”
A later letter from another reader, on February 10, made appropriate comments about the original article and the first letter. What do you think was said in the second letter?
Centroid of triangle—E. A triangular plate held vertically in a liquid has one edge (of length B) coincident with the surface of the liquid; the altitude of the plate is H. Derive an expression for the depth of the centroid. What is the horizontal force exerted by the liquid, whose density is ρ, on one side of the plate?
Blake-Kozeny equation—E. The Blake-Kozeny equation for the pressure drop (p1 – p2) in laminar flow of a fluid of viscosity μ through a packed bed of length L, particle diameter Dp and void fraction ε is (Section 4.4):
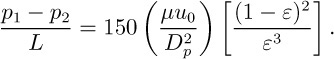
Giving your reasons, suggest appropriate units for ε.
If p1 – p2 = 75 lbf/in2, Dp = 0.1 in., L = 6.0 ft, μ = 0.22 P, and u0 = 0.1 ft/s, compute the value of ε.
Shear stresses for air and water—E. Consider the situation in Fig. 1.8, with h = 0.1 cm and V = 1.0 cm/s. The pressure is atmospheric throughout.
If the fluid is air at 20 °C, evaluate the shear stress τa (dynes/cm2). Does τ vary across the gap? Explain.
Evaluate τw if the fluid is water at 20 °C. What is the ratio τw/τa?
If the temperature is raised to 80 °C, does τa increase or decrease? What about τw?
True/false. Check true or false, as appropriate:14
)
)
)
)
)
)
)
(a) |
When a fluid is subjected to a steady shear stress, it will reach a state of equilibrium in which no further motion occurs. |
T □ F □ |
(b) |
Pressure and shear stress are two examples of a force per unit area. |
T □ F □ |
(c) |
In fluid mechanics, the basic conservation laws are those of volume, energy, and momentum. |
T □ F □ |
(d) |
Absolute pressures and temperatures must be employed when using the ideal gas law. |
T □ F □ |
(e) |
The density of an ideal gas depends only on its absolute temperature and its molecular weight. |
T □ F □ |
(f) |
Closely, the density of water is 1,000 kg/m3, and the gravitational acceleration is 9.81 m/s2. |
T □ F □ |
(g) |
To convert pressure from gauge to absolute, add approximately 1.01 Pa. |
T □ F □ |
(h) |
To convert from psia to psig, add 14.7, approximately. |
T □ F □ |
(i) |
The absolute atmospheric pressure in the classroom is roughly one bar. |
T □ F □ |
(j) |
If ρ is density in g/cm3 and μ is viscosity in g/cm s, then the kinematic viscosity ν = μ/ρ is in stokes. |
T □ F □ |
(k) |
For a given liquid, surface tension and surface energy per unit area have identical numerical values and identical units. |
T □ F □ |
(l) |
A force is equivalent to a rate of transfer of momentum. |
T □ F □ |
(m) |
Work is equivalent to a rate of dissipation of power per unit time. |
T □ F □ |
(n) |
It is possible to have gauge pressures that are as low as –20.0 psig. |
T □ F □ |
(o) |
The density of air in the classroom is roughly 0.08 kg/m3. |
T □ F □ |
(p) |
Pressure in a static fluid varies in the vertically upward direction z according to dp/dz = −ρgc. |
T □ F □ |
(q) |
At any point, the rate of change of pressure with elevation is dp/dz = −ρg, for both incompressible and compressible fluids. |
T □ F □ |
(r) |
A vertical pipe full of water, 34 ft high and open at the top, will generate a pressure of about one atmosphere (gauge) at its base. |
T □ F □ |
(s) |
The horizontal force on one side of a vertical circular disk of radius R immersed in a liquid of density ρ, with its center a distance R below the free surface, is πR3ρg. |
T □ F □ |
(t) |
For a vertical rectangle or dam of width W and depth D, with its top edge submerged in a liquid of density ρ, as in Fig. 1.15, the total horizontal thrust of the liquid can also be expressed as |
T □ F □ |
(u) |
The horizontal pressure force on a rectangular dam with its top edge in the free surface is Fx. If the dam were made twice as deep, but still with the same width, the total force would be 2Fx. |
T □ F □ |
(v) |
A solid object completely immersed in oil will experience the same upward buoyant force as when it is immersed in water. |
T □ F □ |
(w) |
Archimedes’ law will not be true if the object immersed is hollow (such as an empty box with a tight lid, for example). |
T □ F □ |
(x) |
The rate of pressure change due to centrifugal action is given by ∂p/∂r = ρr2ω, in which ω is the angular velocity of rotation. |
T □ F □ |
(y) |
To convert radians per second into rpm, divide by 120π. |
T □ F □ |
(z) |
The shape of the free surface of a liquid in a rotating container is a hyperbola. |
T □ F □ |
(A) |
The hydrostatic force exerted on one face of a square plate of side L that is held vertically in a liquid with one edge in the free surface is F. If the plate is lowered vertically by a distance L, the force on one face will be 3F. |
T □ F □ |
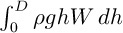, where h is the coordinate measured downward from the free surface.){kind=link}
){kind=link}
){kind=link}
){kind=link}
){kind=link}
){kind=link}
){kind=link}
){kind=link}
){kind=link}