This chapter is from the book
This chapter is from the book
This chapter is from the book
Orthogonal Coding
A third useful type of coding, besides dummy coding and effect coding, is orthogonal coding. You can use orthogonal coding in both planned and post hoc situations. I’ll be discussing planned orthogonal coding (also termed planned orthogonal contrasts) here, because this approach is most useful when you already know something about how your variables work, and therefore are in a position to specify in advance which comparisons you will want to make.
Establishing the Contrasts
Orthogonal coding (I’ll explain the term orthogonal shortly) depends on a matrix of values that define the contrasts that you want to make. Suppose that you plan an experiment with five groups: say, four treatments and a control. To define the contrasts that interest you, you set up a matrix such as the one shown in Figure 7.13.
)
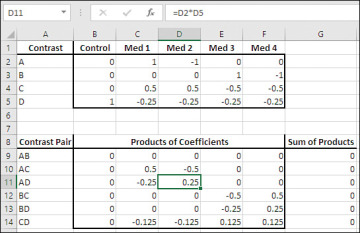
Figure 7.13 The sums of products in G9:G14 satisfy the condition of orthogonality.
In orthogonal coding, just defining the contrasts isn’t enough. Verifying that the contrasts are orthogonal to one another is also necessary. One fairly tedious way to verify that is also shown in Figure 7.13. The range B9:F14 contains the products of corresponding coefficients for each pair of contrasts defined in B2:F5. So row 10 tests Contrasts A and C, and the coefficients in row 2 and row 4 are multiplied to get the products in row 10. For example, the formula in cell C10 is:
=C2*C4
In row 11, testing Contrast A with Contrast D, cell D11 contains this formula:
=D2*D5
Finally, total up the cells in each row of the matrix of coefficient products. If the total is 0, those two contrasts are orthogonal to one another. This is done in the range G9:G14. All the totals in that range are 0, so each of the contrasts defined in B2:F5 are orthogonal to one another.
Planned Orthogonal Contrasts Via ANOVA
Figure 7.14 shows how the contrast coefficients are used in the context of an ANOVA. I’m inflicting this on you to give you a greater appreciation of how much easier the regression approach makes all this.
)
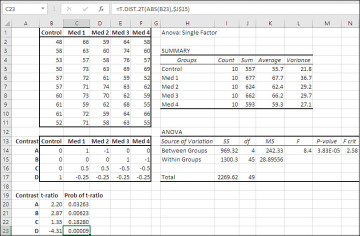
Figure 7.14 The calculation of the t-ratios involves the group means and counts, the mean square within and the contrast coefficients.
Figure 7.14 shows a new data set, laid out for analysis by the ANOVA: Single Factor tool. That tool has been run on the data, and the results are shown in H1:N17. The matrix of contrast coefficients, which has already been tested for orthogonality, is in the range B14:F17. Each of these is needed to compute the t-ratios that test the significance of the difference established in each contrast.
The formulas to calculate the t-ratios are complex. Here’s the formula for the first contrast, Contrast A, which tests the difference between the mean of the Med 1 group and the Med 2 group:
=SUMPRODUCT(B14:F14,TRANSPOSE($K$5:$K$9))/SQRT($K$15*SUM(B14:F14^2/TRANSPOSE($I$5:$I$9)))
The formula must be array-entered using Ctrl+Shift+Enter. Here it is in general form, using summation notation:
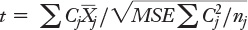
where:
Cj is the contrast coefficient for the jth mean.
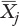is the jth sample mean.MSE is the mean square error from the ANOVA table. If you don’t want to start by running an ANOVA, just take the average of the sample group variances. In this case, MSE is picked up from cell K15, calculated and reported by the Data Analysis tool.
nj is the number of observations in the jth sample.
The prior two formulas, in Excel and summation syntax, are a trifle more complicated than they need be. They allow for unequal sample sizes. As you’ll see in the next section, unequal sample sizes generally—not always—result in nonorthogonal contrasts. If you have equal sample sizes, the formulas can treat the sample sizes as a constant and simplify as a result.
Returning to Figure 7.14, notice the t-ratios and associated probability levels in the range B20:C23. Each of the t-ratios is calculated using the Excel array formula just given, adjusted to pick up the contrast coefficients for different contrasts.
The probabilities are returned by the T.DIST.2T() function, the non-directional version of the t-test. The probability informs you how much of the area under the t-distribution with 45 degrees of freedom is to the left of, in the case of Contrast A, −2.20 and to the right of +2.20. If you had specified alpha as 0.01 prior to seeing the data, you could reject the null hypothesis of no population difference for Contrast B and Contrast D. The probabilities of the associated t-ratios occurring by chance in a central t distribution are lower than your alpha level. The probabilities for Contrast A and Contrast C are higher than alpha and you must retain the associated null hypotheses.
Planned Orthogonal Contrasts Using LINEST()
As far as I’m concerned, there’s a lot of work—and opportunity to make mistakes—involved with planned orthogonal contrasts in the context of the traditional ANOVA. Figure 7.15 shows how much easier things are using regression, and in an Excel worksheet that means LINEST().
)
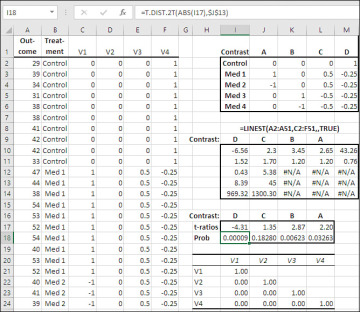
Figure 7.15 With orthogonal coding, the regression coefficients and their standard errors do most of the work for you.
Using regression, you still need to come up with the orthogonal contrasts and their coefficients. But they’re the same ones needed for the ANOVA approach. Figure 7.15 repeats them, transposed from Figure 7.14, in the range I1:M6.
The difference with orthogonal coding and regression, as distinct from the traditional ANOVA approach shown in Figure 7.14, is that you use the coefficients to populate the vectors, just as you do with dummy coding (1’s and 0’s) and effect coding (1’s, 0’s, and −1’s). Each vector represents a contrast and the values in the vector are the contrast’s coefficients, each associated with a different group.
So, in Figure 7.15, Vector 1 in Column C has 0’s for the Control group, 1’s for Med 1, −1’s for Med 2, and—although you can’t see them in the figure—0’s for Med 3 and Med 4. Those are the values called for in Contrast A, in the range J2:J6. Similar comments apply to vectors 2 through 4. The vectors make the contrast coefficients a formal part of the analysis.
The regression approach also allows for a different slant on the notion of orthogonality. Notice the matrix of values in the range I21:L24. It’s a correlation matrix showing the correlations between each pair of vectors in columns C through F. Notice that each vector has a 0.0 correlation with each of the other vectors. They are independent of one another. That’s another way of saying that if you plotted them, their axes would be at right angles to one another (orthogonal means right angled).
Planned orthogonal contrasts have the greatest amount of statistical power of any of the multiple comparison methods. That means that planned orthogonal contrasts are more likely to identify true population differences than the alternatives (such as Dunnett and Scheffé). However, they require that you be able to specify your hypotheses in the form of contrasts before the experiment, and that you are able to obtain equal group sizes. If you add even one observation to any of the groups, the correlations among the vectors will no longer be 0.0, you’ll have lost the orthogonality, and you’ll need to resort to (probably) planned nonorthogonal contrasts, which, other things equal, are less powerful.
It’s easy to set up the vectors using the general VLOOKUP() approach described earlier in this chapter. For example, this formula is used to populate Vector 1:
=VLOOKUP($B2,$I$2:$M$6,2,0)
It’s entered in cell C2 and can be copied and pasted into columns D through F (you’ll need to adjust the third argument from 2 to 3, 4 and 5). Then make a multiple selection of C2:F2 and drag down through the end of the Outcome values.
With the vectors established, array-enter this LINEST() formula into a five-row by five-column range:
=LINEST(A2:A51,C2:F51,,TRUE)
You now have the regression coefficients and their standard errors. The t-ratios—the same ones that show up in the range B20:B23 of Figure 7.14—are calculated by dividing a regression coefficient by its standard error. So the t-ratio in cell L17 of Figure 7.15 is returned by this formula:
=L10/L11
The coefficients and standard errors come back from LINEST() in reverse of the order that you would like, so the t-ratios are in reverse order, too. However, if you compare them to the t-ratios in Figure 7.14, you’ll find that their values are precisely the same. You calculate the probabilities associated with the t-ratios just as in Figure 7.14, using the T.DIST() function that’s appropriate to the sort of research hypothesis (directional or nondirectional) that you would specify at the outset.