- Random Numbers and Probability Distributions
- Casino Royale: Roll the Dice
- Normal Distribution
- The Student Who Taught Everyone Else
- Statistical Distributions in Action
- Hypothetically Yours
- The Mean and Kind Differences
- Worked-Out Examples of Hypothesis Testing
- Exercises for Comparison of Means
- Regression for Hypothesis Testing
- Analysis of Variance
- Significantly Correlated
- Summary
This chapter is from the book
This chapter is from the book
This chapter is from the book
The Student Who Taught Everyone Else
The other commonly used distribution is the Student’s t-distribution, which was specified by William Sealy Gosset. He published a paper in Biometrika in 1908 under the pseudonym, Student. Gosset worked for the Guinness Brewery in Durbin, Ireland, where he worked with small samples of barley.
Mr. Gosset is the unsung hero of statistics. He published his work under a pseudonym because of the restrictions from his employer. Apart from his published work, his other contributions to statistical analysis are equally significant. The Cult of Statistical Significance, a must read for anyone interested in data science, chronicles Mr. Gosset’s work and how other influential statisticians of the time, namely Ronald Fisher and Egon Pearson, by way of their academic bona fides ended up being more influential than the equally deserving Mr. Gosset.
The t-distribution refers to a family of distributions that deal with the mean of a normally distributed population with small sample sizes and unknown population standard deviation. The Normal distribution describes the mean for a population, whereas the t-distribution describes the mean of samples drawn from the population. The t-distribution for each sample could be different and the t-distribution resembles the normal distribution for large sample sizes.
In Figure 6.7, I plot t-distributions for various sample sizes, also known as the degrees of freedom, along with the normal distribution. Note that the t-distribution with a sample size of 30 resembles the normal distribution the most.
)
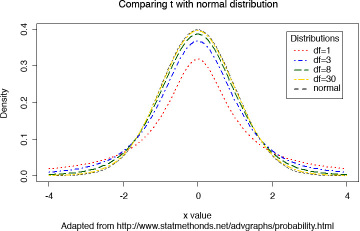
Figure 6.7 Probability distribution curves for normal and t-distributions for different sample sizes
Over the years, 30 has emerged as the preferred threshold for a large enough sample that may prompt one to revert to the Normal distribution. Many researchers, though, question the suitability of 30 as the threshold. In the world of big data, 30 obviously seems awfully small.