- Key-indexed counting
- LSD string sort
- MSD string sort
- Three-way string quicksort
- Which string-sorting algorithm should I use?
- Q&A
- Exercises
- CREATIVE PROBLEMS
- EXPERIMENTS
Three-way string quicksort
We can also adapt quicksort to MSD string sorting by using 3-way partitioning on the leading character of the keys, moving to the next character on only the middle subarray (keys with leading character equal to the partitioning character). This method is not difficult to implement, as you can see in Algorithm 5.3: we just add an argument to the recursive method in Algorithm 2.5 that keeps track of the current character, adapt the 3-way partitioning code to use that character, and appropriately modify the recursive calls.

Figure 5.15 Overview of 3-way string quicksort
Although it does the computation in a different order, 3-way string quicksort amounts to sorting the array on the leading characters of the keys (using quicksort), then applying the method recursively on the remainder of the keys. For sorting strings, the method compares favorably with normal quicksort and with MSD string sort. Indeed, it is a hybrid of these two algorithms.
Three-way string quicksort divides the array into only three parts, so it involves more data movement than MSD string sort when the number of nonempty partitions is large because it has to do a series of 3-way partitions to get the effect of the multiway partition. On the other hand, MSD string sort can create large numbers of (empty) subarrays, whereas 3-way string quicksort always has just three. Thus, 3-way string quicksort adapts well to handling equal keys, keys with long common prefixes, keys that fall into a small range, and small arrays—all situations where MSD string sort runs slowly. Of particular importance is that the partitioning adapts to different kinds of structure in different parts of the key. Also, like quicksort, 3-way string quicksort does not use extra space (other than the implicit stack to support recursion), which is an important advantage over MSD string sort, which requires space for both frequency counts and an auxiliary array.

Figure 5.16 Typical 3-way string quicksort candidate
The figure at the bottom of this page shows all of the recursive calls that Quick3string makes for our example. Each subarray is sorted using precisely three recursive calls, except when we skip the recursive call on reaching the ends of the (equal) string(s) in the middle subarray.
As usual, in practice, it is worthwhile to consider various standard improvements to the implementation in Algorithm 5.3:
Small subarrays.
In any recursive algorithm, we can gain efficiency by treating small subarrays differently. In this case, we use the insertion sort from page 715, which skips the characters that are known to be equal. The improvement due to this change is likely to be significant, though not nearly as important as for MSD string sort.
Restricted alphabet.
To handle specialized alphabets, we could add an Alphabet argument alpha to each of the methods and replace s.charAt(d) with alpha.toIndex(s.charAt(d)) in charAt(). In this case, there is no benefit to doing so, and adding this code is likely to substantially slow the algorithm down because this code is in the inner loop.
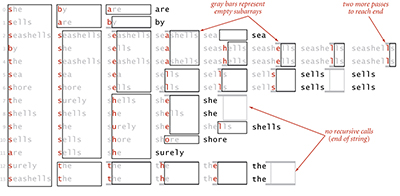
Figure 5.17 Trace of recursive calls for 3-way string quicksort (no cuto˜ for small subarrays)
Randomization.
As with any quicksort, it is generally worthwhile to shuffle the array beforehand or to use a random paritioning item by swapping the first item with a random one. The primary reason to do so is to protect against worst-case performance in the case that the array is already sorted or nearly sorted.
For string keys, standard quicksort and all the other sorts in Chapter 2 are actually MSD string sorts, because the compareTo() method in String accesses the characters in left-to-right order. That is, compareTo() accesses only the leading characters if they are different, the leading two characters if the first characters are the same and the second different, and so forth. For example, if the first characters of the strings are all different, the standard sorts will examine just those characters, thus automatically realizing some of the same performance gain that we seek in MSD string sorting. The essential idea behind 3-way quicksort is to take special action when the leading characters are equal. Indeed, one way to think of Algorithm 5.3 is as a way for standard quicksort to keep track of leading characters that are known to be equal. In the small subarrays, where most of the compares in the sort are done, the strings are likely to have numerous equal leading characters. The standard algorithm has to scan over all those characters for each compare; the 3-way algorithm avoids doing so.
Performance.
Consider a case where the string keys are long (and are all the same length, for simplicity), but most of the leading characters are equal. In such a situation, the running time of standard quicksort is proportional to the string length times 2N ln N, whereas the running time of 3-way string quicksort is proportional to N times the string length (to discover all the leading equal characters) plus 2N ln N character comparisons (to do the sort on the remaining short keys). That is, 3-way string quicksort requires up to a factor of 2lnN fewer character compares than normal quicksort. It is not unusual for keys in practical sorting applications to have characteristics similar to this artificial example.
Proposition E. To sort an array of N random strings, 3-way string quicksort uses ~ 2N ln N character compares, on the average.
Proof: There are two instructive ways to understand this result. First, considering the method to be equivalent to quicksort partitioning on the leading character, then (recursively) using the same method on the subarrays, we should not be surprised that the total number of operations is about the same as for normal quicksort—but they are single-character compares, not full-key compares. Second, considering the method as replacing key-indexed counting by quicksort, we expect that the N log R N running time from Proposition D should be multiplied by a factor of 2 ln R because it takes quicksort 2R ln R steps to sort R characters, as opposed to R steps for the same characters in the MSD string sort. We omit the full proof.
As emphasized on page 718, considering random strings is instructive, but more detailed analysis is needed to predict performance for practical situations. Researchers have studied this algorithm in depth and have proved that no algorithm can beat 3-way string quicksort (measured by number of character compares) by more than a constant factor, under very general assumptions. To appreciate its versatility, note that 3-way string quicksort has no direct dependencies on the size of the alphabet.
Example: web logs.
As an example where 3-way string quicksort shines, we can consider a typical modern data-processing task. Suppose that you have built a website and want to analyze the traffic that it generates. You can have your system administrator supply you with a web log of all transactions on your site. Among the information associated with a transaction is the domain name of the originating machine. For example, the file week.log.txt on the booksite is a log of one week’s transactions on our booksite. Why does 3-way string quicksort do well on such a file? Because the sorted result is replete with long common prefixes that this method does not have to reexamine.

