15.2. High-Level Design Overview
We start with a high-level design in this section. We’ll then pause to address the practical issues of our programming infrastructure before reducing that high-level design to the specific sampling strategies.
15.2.1. Scattering
Light that enters the camera and is measured arrives from points on surfaces in the scene that either scattered or emitted the light. Those points lie along the rays that we choose to sample for our measurement. Specifically, the points casting light into the camera are the intersections in the scene of rays, whose origins are points on the image plane, that passed through the camera’s aperture.
To keep things simple, we assume a pinhole camera with a virtual image plane in front of the center of projection, and an instantaneous exposure. This means that there will be no blur in the image due to defocus or motion. Of course, an image with a truly zero-area aperture and zero-time exposure would capture zero photons, so we take the common graphics approximation of estimating the result of a small aperture and exposure from the limiting case, which is conveniently possible in simulation, albeit not in reality.
We also assume that the virtual sensor pixels form a regular square grid and estimate the value that an individual pixel would measure using a single sample at the center of that pixel’s square footprint. Under these assumptions, our sampling rays are the ones with origins at the center of projection (i.e., the pinhole) and directions through each of the sensor-pixel centers.1
Finally, to keep things simple we chose a coordinate frame in which the center of projection is at the origin and the camera is looking along the negative z-axis. We’ll also refer to the center of projection as the eye. See Section 15.3.3 for a formal description and Figure 15.1 for a diagram of this configuration.
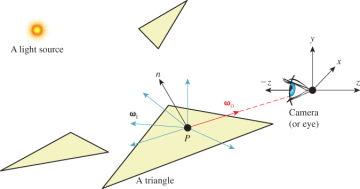
Figure 15.1: A specific surface location P that is visible to the camera, incident light at P from various directions {ωi}, and the exitant direction ωo toward the camera.
The light that arrived at a specific sensor pixel from a scene point P came from some direction. For example, the direction from the brightest light source in the scene provided a lot of light. But not all light arrived from the brightest source. There may have been other light sources in the scene that were dimmer. There was also probably a lot of light that previously scattered at other points and arrived at P indirectly. This tells us two things. First, we ultimately have to consider all possible directions from which light may have arrived at P to generate a correct image. Second, if we are willing to accept some sampling error, then we can select a finite number of discrete directions to sample. Furthermore, we can probably rank the importance of those directions, at least for lights, and choose a subset that is likely to minimize sampling error.
Let’s start by considering all possible directions for incoming light in pseudocode and then return to the ranking of discrete directions when we later need to implement directional sampling concretely.
To consider the points and directions that affect the image, our program has to look something like Listing 15.1.
Listing 15.1: High-level rendering structure.
1 for each visible point P with direction ωo from it to pixel center (x, y): 2 sum = 0 3 for each incident light direction ωi at P: 4 sum += light scattered at P from ωi to ωo 5 pixel[x, y] = sum
15.2.2. Visible Points
Now we devise a strategy for representing points in the scene, finding those that are visible and scattering the light incident on them to the camera.
For the scene representation, we’ll work within some of the common rendering approximations described in Chapter 14. None of these are so fundamental as to prevent us from later replacing them with more accurate models.
Assume that we only need to model surfaces that form the boundaries of objects. “Object” is a subjective term; a surface is technically the interface between volumes with homogeneous physical properties. Some of these objects are what everyday language recognizes as such, like a block of wood or the water in a pool. Others are not what we are accustomed to considering as objects, such as air or a vacuum.
We’ll model these surfaces as triangle meshes. We ignore the surrounding medium of air and assume that all the meshes are closed so that from the outside of an object one can never see the inside. This allows us to consider only single-sided triangles. We choose the convention that the vertices of a triangular face, seen from the outside of the object, are in counterclockwise order around the face. To approximate the shading of a smooth surface using this triangle mesh, we model the surface normal at a point on a triangle pointing in the direction of the barycentric interpolation of prespecified normal vectors at its vertices. These normals only affect shading, so silhouettes of objects will still appear polygonal.
Chapter 27 explores how surfaces scatter light in great detail. For simplicity, we begin by assuming all surfaces scatter incoming light equally in all directions, in a sense that we’ll make precise presently. This kind of scattering is called Lambertian, as you saw in Chapter 6, so we’re rendering a Lambertian surface. The color of a surface is determined by the relative amount of light scattered at each wavelength, which we represent with a familiar RGB triple.
This surface mesh representation describes all the potentially visible points at the set of locations {P}. To render a given pixel, we must determine which potentially visible points project to the center of that pixel. We then need to select the scene point closest to the camera. That point is the actually visible point for the pixel center. The radiance—a measure of light that’s defined precisely in Section 26.7.2, and usually denoted with the letter L—arriving from that point and passing through the pixel is proportional to the light incident on the point and the point’s reflectivity.
To find the nearest potentially visible point, we first convert the outer loop of Listing 15.1 (see the next section) into an iteration over both pixel centers (which correspond to rays) and triangles (which correspond to surfaces). A common way to accomplish this is to replace “for each visible point” with two nested loops, one over the pixel centers and one over the triangles. Either can be on the outside. Our choice of which is the new outermost loop has significant structural implications for the rest of the renderer.
15.2.3. Ray Casting: Pixels First
Listing 15.2: Ray-casting pseudocode.
1 for each pixel position (x, y): 2 let R be the ray through (x, y) from the eye 3 for each triangle T: 4 let P be the intersection of R and T (if any) 5 sum = 0 6 for each direction: 7 sum += . . . 8 if P is closer than previous intersections at this pixel: 9 pixel[x, y] = sum
Consider the strategy where the outermost loop is over pixel centers, shown in Listing 15.2. This strategy is called ray casting because it creates one ray per pixel and casts it at every surface. It generalizes to an algorithm called ray tracing, in which the innermost loop recursively casts rays at each direction, but let’s set that aside for the moment.
Ray casting lets us process each pixel to completion independently. This suggests parallel processing of pixels to increase performance. It also encourages us to keep the entire scene in memory, since we don’t know which triangles we’ll need at each pixel. The structure suggests an elegant way of eventually processing the aforementioned indirect light: Cast more rays from the innermost loop.
15.2.4. Rasterization: Triangles First
Now consider the strategy where the outermost loop is over triangles shown in Listing 15.3. This strategy is called rasterization, because the inner loop is typically implemented by marching along the rows of the image, which are called rasters. We could choose to march along columns as well. The choice of rows is historical and has to do with how televisions were originally constructed. Cathode ray tube (CRT) displays scanned an image from left to right, top to bottom, the way that English text is read on a page. This is now a widespread convention: Unless there is an explicit reason to do otherwise, images are stored in row-major order, where the element corresponding to 2D position (x, y) is stored at index (x + y * width) in the array.
Listing 15.3: Rasterization pseudocode; O denotes the origin, or eyepoint.
1 for each pixel position (x, y): 2 closest[x, y] = ∞ 3 4 for each triangle T: 5 for each pixel position (x, y): 6 let R be the ray through (x, y) from the eye 7 let P be the intersection of R and T 8 if P exists: 9 sum = 0 10 for each direction: 11 sum += . . . 12 if the distance to P is less than closest[x, y]: 13 pixel[x, y] = sum 14 closest[x, y] = |P - O|
Rasterization allows us to process each triangle to completion independently.2 This has several implications. It means that we can render much larger scenes than we can hold in memory, because we only need space for one triangle at a time. It suggests triangles as the level of parallelism. The properties of a triangle can be maintained in registers or cache to avoid memory traffic, and only one triangle needs to be memory-resident at a time. Because we consider adjacent pixels consecutively for a given triangle, we can approximate derivatives of arbitrary expressions across the surface of a triangle by finite differences between pixels. This is particularly useful when we later become more sophisticated about sampling strategies because it allows us to adapt our sampling rate to the rate at which an underlying function is changing in screen space.
Note that the conditional on line 12 in Listing 15.3 refers to the closest previous intersection at a pixel. Because that intersection was from a different triangle, that value must be stored in a 2D array that is parallel to the image. This array did not appear in our original pseudocode or the ray-casting design. Because we now touch each pixel many times, we must maintain a data structure for each pixel that helps us resolve visibility between visits. Only two distances are needed for comparison: the distance to the current point and to the previously closest point. We don’t care about points that have been previously considered but are farther away than the closest, because they are hidden behind the closest point and can’t affect the image. The closest array stores the distance to the previously closest point at each pixel. It is called a depth buffer or a z-buffer. Because computing the distance to a point is potentially expensive, depth buffers are often implemented to encode some other value that has the same comparison properties as distance along a ray. Common choices are –zP, the z-coordinate of the point P, and –1/zP. Recall that the camera is facing along the negative z-axis, so these are related to distance from the z = 0 plane in which the camera sits. For now we’ll use the more intuitive choice of distance from P to the origin, |P – O|.
The depth buffer has the same dimensions as the image, so it consumes a potentially significant amount of memory. It must also be accessed atomically under a parallel implementation, so it is a potentially slow synchronization point. Chapter 36 describes alternative algorithms for resolving visibility under rasterization that avoid these drawbacks. However, depth buffers are by far the most widely used method today. They are extremely efficient in practice and have predictable performance characteristics. They also offer advantages beyond the sampling process. For example, the known depth at each pixel at the end of 3D rendering yields a “2.5D” result that enables compositing of multiple render passes and post-processing filters, such as artificial defocus blur.
This depth comparison turns out to be a fundamental idea, and it is now supported by special fixed-function units in graphics hardware. A huge leap in computer graphics performance occurred when this feature emerged in the early 1980s.
