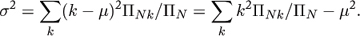This chapter is from the book
This chapter is from the book
This chapter is from the book
1.7. Distributions
In general, probability theory tells us that other facts about the distribution ΠNk of costs are also relevant to our understanding of performance characteristics of an algorithm. Fortunately, for virtually all of the examples that we study in the analysis of algorithms, it turns out that knowing an asymptotic estimate for the average is enough to be able to make reliable predictions. We review a few basic ideas here. Readers not familiar with probability theory are referred to any standard text—for example, [9].
The full distribution for the number of compares used by quicksort for small N is shown in Figure 1.2. For each value of N, the points CNk/N! are plotted: the proportion of the inputs for which quicksort uses k compares. Each curve, being a full probability distribution, has area 1. The curves move to the right, since the average 2NlnN + O(N) increases with N. A slightly different view of the same data is shown in Figure 1.3, where the horizontal axes for each curve are scaled to put the mean approximately at the center and shifted slightly to separate the curves. This illustrates that the distribution converges to a “limiting distribution.”
)
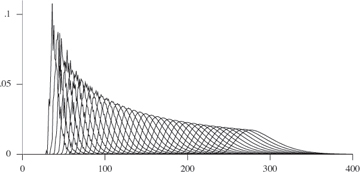
Figure 1.2. Distributions for compares in quicksort, 15 ≤ N ≤ 50
)
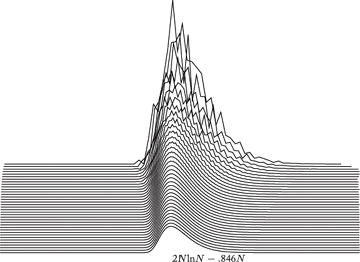
Figure 1.3. Distributions for compares in quicksort, 15 ≤ N ≤ 50 (scaled and translated to center and separate curves)
For many of the problems that we study in this book, not only do limiting distributions like this exist, but also we are able to precisely characterize them. For many other problems, including quicksort, that is a significant challenge. However, it is very clear that the distribution is concentrated near the mean. This is commonly the case, and it turns out that we can make precise statements to this effect, and do not need to learn more details about the distribution.
As discussed earlier, if ΠN is the number of inputs of size N and ΠNk is the number of inputs of size N that cause the algorithm to have cost k, the average cost is given by
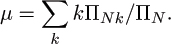
The variance is defined to be
)
The standard deviation σ is the square root of the variance. Knowing the average and standard deviation ordinarily allows us to predict performance reliably. The classical analytic tool that allows this is the Chebyshev inequality: the probability that an observation will be more than c multiples of the standard deviation away from the mean is less than 1/c2. If the standard deviation is significantly smaller than the mean, then, as N gets large, an observed value is very likely to be quite close to the mean. This is often the case in the analysis of algorithms.
Exercise 1.23 What is the standard deviation of the number of compares for the mergesort implementation given earlier in this chapter?
The standard deviation of the number of compares used by quicksort is
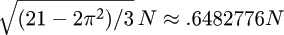
(see §3.9) so, for example, referring to Table 1.1 and taking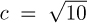 
in Chebyshev’s inequality, we conclude that there is more than a 90% chance that the number of compares when N = 100,000 is within 205,004 (9.2%) of 2,218,033. Such accuracy is certainly adequate for predicting performance.
As N increases, the relative accuracy also increases: for example, the distribution becomes more localized near the peak in Figure 1.3 as N increases. Indeed, Chebyshev’s inequality underestimates the accuracy in this situation, as shown in Figure 1.4. This figure plots a histogram showing the number of compares used by quicksort on 10,000 different random files of 1000 elements. The shaded area shows that more than 94% of the trials fell within one standard deviation of the mean for this experiment.
)
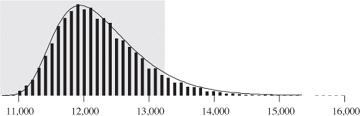
Figure 1.4. Empirical histogram for quicksort compare counts (10,000 trials with N = 1000)
For the total running time, we can sum averages (multiplied by costs) of individual quantities, but computing the variance is an intricate calculation that we do not bother to do because the variance of the total is asymptotically the same as the largest variance. The fact that the standard deviation is small relative to the average for large N explains the observed accuracy of Table 1.1 and Figure 1.1. Cases in the analysis of algorithms where this does not happen are rare, and we normally consider an algorithm “fully analyzed” if we have a precise asymptotic estimate for the average cost and knowledge that the standard deviation is asymptotically smaller.
){kind=link}