1.6. Asymptotic Approximations
The derivation of the average running time of quicksort given earlier yields an exact result, but we also gave a more concise approximate expression in terms of well-known functions that still can be used to compute accurate numerical estimates. As we will see, it is often the case that an exact result is not available, or at least an approximation is far easier to derive and interpret. Ideally, our goal in the analysis of an algorithm should be to derive exact results; from a pragmatic point of view, it is perhaps more in line with our general goal of being able to make useful performance predications to strive to derive concise but precise approximate answers.
To do so, we will need to use classical techniques for manipulating such approximations. In Chapter 4, we will examine the Euler-Maclaurin summation formula, which provides a way to estimate sums with integrals. Thus, we can approximate the harmonic numbers by the calculation
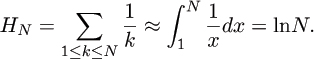
But we can be much more precise about the meaning of ≈, and we can conclude (for example) that HN = lnN + γ + 1/(2N) + O(1/N2) where γ = .57721 ... is a constant known in analysis as Euler’s constant. Though the constants implicit in the O-notation are not specified, this formula provides a way to estimate the value of HN with increasingly improving accuracy as N increases. Moreover, if we want even better accuracy, we can derive a formula for HN that is accurate to within O(N–3) or indeed to within O(N–k) for any constant k. Such approximations, called asymptotic expansions, are at the heart of the analysis of algorithms, and are the subject of Chapter 4.
The use of asymptotic expansions may be viewed as a compromise between the ideal goal of providing an exact result and the practical requirement of providing a concise approximation. It turns out that we are normally in the situation of, on the one hand, having the ability to derive a more accurate expression if desired, but, on the other hand, not having the desire, because expansions with only a few terms (like the one for HN above) allow us to compute answers to within several decimal places. We typically drop back to using the ≈ notation to summarize results without naming irrational constants, as, for example, in Theorem 1.3.
Moreover, exact results and asymptotic approximations are both subject to inaccuracies inherent in the probabilistic model (usually an idealization of reality) and to stochastic fluctuations. Table 1.1 shows exact, approximate, and empirical values for number of compares used by quicksort on random files of various sizes. The exact and approximate values are computed from the formulae given in Theorem 1.3; the “empirical” is a measured average, taken over 100 files consisting of random positive integers less than 106; this tests not only the asymptotic approximation that we have discussed, but also the “approximation” inherent in our use of the random permutation model, ignoring equal keys. The analysis of quicksort when equal keys are present is treated in Sedgewick [28].
Table 1.1. Average number of compares used by quicksort
|
file size |
exact solution |
approximate |
empirical |
|
10,000 |
175,771 |
175,746 |
176,354 |
|
20,000 |
379,250 |
379,219 |
374,746 |
|
30,000 |
593,188 |
593,157 |
583,473 |
|
40,000 |
813,921 |
813,890 |
794,560 |
|
50,000 |
1,039,713 |
1,039,677 |
1,010,657 |
|
60,000 |
1,269,564 |
1,269,492 |
1,231,246 |
|
70,000 |
1,502,729 |
1,502,655 |
1,451,576 |
|
80,000 |
1,738,777 |
1,738,685 |
1,672,616 |
|
90,000 |
1,977,300 |
1,977,221 |
1,901,726 |
|
100,000 |
2,218,033 |
2,217,985 |
2,126,160 |
Exercise 1.20 How many keys in a file of 104 random integers less than 106 are likely to be equal to some other key in the file? Run simulations, or do a mathematical analysis (with the help of a system for mathematical calculations), or do both.
Exercise 1.21 Experiment with files consisting of random positive integers less than M for M = 10,000, 1000, 100 and other values. Compare the performance of quick-sort on such files with its performance on random permutations of the same size. Characterize situations where the random permutation model is inaccurate.
Exercise 1.22 Discuss the idea of having a table similar to Table 1.1 for mergesort.
In the theory of algorithms, O-notation is used to suppress detail of all sorts: the statement that mergesort requires O(NlogN) compares hides everything but the most fundamental characteristics of the algorithm, implementation, and computer. In the analysis of algorithms, asymptotic expansions provide us with a controlled way to suppress irrelevant details, while preserving the most important information, especially the constant factors involved. The most powerful and general analytic tools produce asymptotic expansions directly, thus often providing simple direct derivations of concise but accurate expressions describing properties of algorithms. We are sometimes able to use asymptotic estimates to provide more accurate descriptions of program performance than might otherwise be available.

