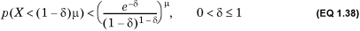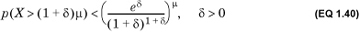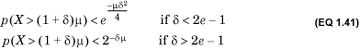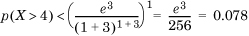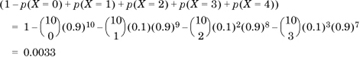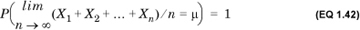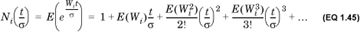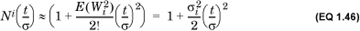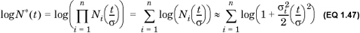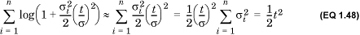1.7. Useful Theorems
This section discusses some useful theorems: Markov’s and Chebyshev’s inequality theorems allow us to bound the amount of mass in the tail of a distribution, knowing nothing more than its expected value (Markov) and variance (Chebyshev). Chernoff’s bound allows us to bound both the lower and upper tails of distributions arising from independent trials. The law of large numbers allows us to relate realworld measurements with the expectation of a random variable. Finally, the central limit theorem shows why so many real-world random variables are normally distributed.
1.7.1. Markov’s Inequality
If X is a non-negative random variable with mean μ, then for any constant α > 0,

Thus, we can bound the probability mass to the right of any constant a by a value proportional to the expected value of X and inversely proportional to a (Figure 1.7). Markov’s inequality requires knowledge only of the mean of the distribution. Note that this inequality is trivial if α < μ (why?). Note also that the Markov inequality does not apply to some standard distributions, such as the normal distribution, because they are not always non-negative.
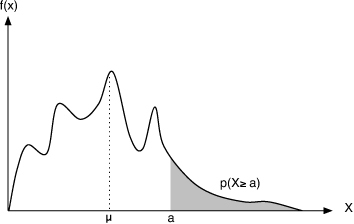
Figure 1.7. Markov’s inequality
1.7.2. Chebyshev’s Inequality
If X is a random variable with a finite mean μ and variance σ2, then for any constant α > 0,

Chebyshev’s inequality bounds the “tails” of a distribution on both sides of the mean, given the variance. Roughly, the farther away we get from the mean (the larger a is), the less mass there is in the tail (because the right-hand size decreases by a factor quadratic in a), as shown in Figure 1.8.
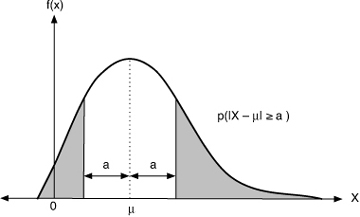
Figure 1.8. Chebyshev’s inequality
1.7.3. Chernoff Bound
Let the random variable Xi denote the outcome of the ith iteration of a process, with Xi = 1 denoting success and Xi = 0 denoting failure. Assume that the probability of success of each iteration is independent of the others (this is critical!). Denote the probability of success of the ith trial by p(Xi =1) =pi. Let X be the number of successful trials in a run of n trials. Clearly,
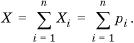
Let E[X] = μ be the expected value of X (the expected number of successes). Then, we can state two Chernoff bounds that tell us the probability that there are too few or too many successes.
The lower bound is given by
This is somewhat hard to compute. A weaker but more tractable bound is
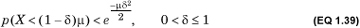
Note that both equations bound the area under the density distribution of X between –∞ and (1 – δ)μ. The second form makes it clear that the probability of too few successes declines quadratically with δ.
The upper bound is given by
A weaker but more tractable bound is
1.7.4. Strong Law of Large Numbers
The law of large numbers relates the sample mean—the average of a set of observations of a random variable—with the population, or true mean, which is its expected value. The strong law of large numbers, the better-known variant, states that if X1, X2,..., Xn are n independent, identically distributed random variables with the same expected value μ, then
No matter how X is distributed, by computing an average over a sufficiently large number of observations, this average can be made to be as close to the true mean as we wish. This is the basis of a variety of statistical techniques for hypothesis testing, as described in Chapter 2.
We illustrate this law in Figure 1.9, which shows the average of 1,2,3,..., 500 successive values of a random variable drawn from a uniform distribution in the range [0, 1]. The expected value of this random variable is 0.5, and the average converges to this expected value as the sample size increases.
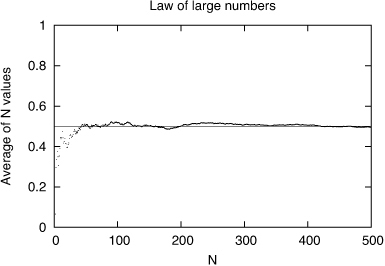
Figure 1.9. Strong law of large numbers: As N increases, the average value of sample of N random values converges to the expected value of the distribution.
1.7.5. Central Limit Theorem
The central limit theorem deals with the sum of a large number of independent random variables that are arbitrarily distributed. The theorem states that no matter how each random variable is distributed, as long as its contribution to the total is small, the sum is well described by a Gaussian random variable.
More precisely, let X1, X2,..., Xn be n independent, identically distributed random variables, each with a finite mean μ and variance σ2. Then, the distribution of the normalized sum given by 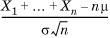 tends to the standard (0,1) normal as n → ∞. The central limit theorem is the reason why the Gaussian distribution is the limit of the binomial distribution.
tends to the standard (0,1) normal as n → ∞. The central limit theorem is the reason why the Gaussian distribution is the limit of the binomial distribution.
In practice, the central limit theorem allows us to model aggregates by a Gaussian random variable if the size of the aggregate is large and the elements of the aggregate are independent.
The Gaussian distribution plays an important role in statistics because of the central limit theorem. Consider a set of measurements of a physical system. Each measurement can be modeled as an independent random variable whose mean and variance are those of the population. From the central limit theorem, their sum, and therefore their mean, which is just the normalized sum, is approximately normally distributed. As we will study in Chapter 2, this allows us to infer the population mean from the sample mean, which forms the foundation of statistical confidence. We now prove the central limit theorem by using MGFs.
The proof proceeds in three stages. First, we compute the MGF of the sum of n random variables in terms of the MGFs of each of the random variables. Second, we find a simple expression for the MGF of a random variable when the variance is large: a situation we expect when adding together many independent random variables. Finally, we plug this simple expression back into the MGF of the sum to obtain the desired result.
Consider a random variable Y = X1 + X2 + ... + Xn, the sum of n independent random variables Xi. Let μi and σi denote the mean and standard deviation of Xi, and let μ and σ denote the mean and standard deviation of Y. Because all the Xis are independent,

Define the random variable Wi to be (Xi – μi): It represents the distance of an instance of the random variable Xi from its mean. By definition, the rth moment of Wi about the origin is the rth moment of Xi about its mean. Also, because the Xi are independent, so are the Wi. Denote the MGF of Xi by Mi(t) and the MGF of Wi by Ni(t).
Note that Y – μ= X1 + X2 + ... + Xn – Σμi = Σ(Xi – μi) = ΣWi. So, the MGF of Y – μ is the product of the MGFs of the 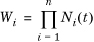 . Therefore, the MGF of (Y – μ)/σ denoted N*(t) is given by
. Therefore, the MGF of (Y – μ)/σ denoted N*(t) is given by

Consider the MGF Ni(t/σ), which is given by 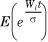 . Expanding the exponential, we find that
. Expanding the exponential, we find that
Now, E(Wi) = E(Xi – μi) = E(Xi) – μi = μi – μi = 0, so we can ignore the second term in the expansion. Recall that σ is the standard deviation of the sum of n random variables. When n is large, so too is σ, which means that, to first order, we can ignore terms that have σ 3 and higher powers of σ in the denominator in Equation 1.45. Therefore, for large n, we can write
where we have used the fact that 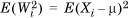 which is the variance of
which is the variance of 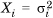 .
.
Returning to the expression in Equation 1.44, we find that
It is easily shown by the Taylor series expansion that when h is small—so that h2 and higher powers of h can be ignored—log(1+h) can be approximated by h. So, when n is large and σ is large, we can further approximate
where, for the last simplification, we used Equation 1.43. Thus, log N*(t) is approximately 1/2 t2, which means that

But this is just the MGF of a standard normal variable with 0 mean and a variance of 1 (Equation 1.32). Therefore, (Y – μ)/σ is a standard normal variable, which means that Y~N(μ, σ2). We have therefore shown that the sum of a large number of independent random variables is distributed as a normal variable whose mean is the sum of the individual means and whose variance is the sum of the individual variances (Equation 1.43), as desired.
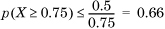 . The actual probability mass is only 0.25, so the Markov bound is quite loose. This is typical of a Markov bound.
. The actual probability mass is only 0.25, so the Markov bound is quite loose. This is typical of a Markov bound.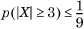 , so that
, so that 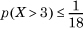 , or about 5.5%. Compare this to the tight bound of 0.135% (Section 1.6.2).
, or about 5.5%. Compare this to the tight bound of 0.135% (Section 1.6.2).