This chapter is from the book
This chapter is from the book
This chapter is from the book
1.5. Standard Discrete Distributions
We now present some discrete distributions that frequently arise when studying networking problems.
1.5.1. Bernoulli Distribution
A discrete random variable X is called a Bernoulli random variable if it can take only two values, 0 or 1, and its probability mass function is defined as p(0) = 1 – a and p(1) = a. We can think of X as representing the result of some experiment, with X=1 being success, with probability a. The expected value of a Bernoulli random variable is a and variance is p(1 – a).
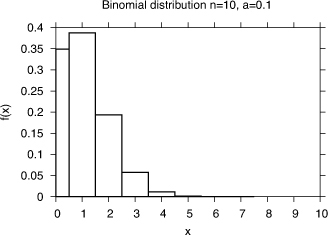
1.5.2. Binomial Distribution
Consider a series of n Bernoulli experiments where the result of each experiment is independent of the others. We would naturally like to know the number of successes in these n trials. This can be represented by a discrete random variable X with parameters (n,a) and is called a binomial random variable. The probability mass function of a binomial random variable with parameters (n,a) is given by
If we set b = 1 – a, then these are just the terms of the expansion (a + b)n. The expected value of a variable that is binomially distributed with parameters (n,a) is na.
Example 1.29. Binomial Random Variable
Consider a local area network with ten stations. Assume that, at a given moment, each node can be active with probability p = 0.1. What is the probability that (a) one station is active, (b) five stations are active, (c) all ten stations are active?
Solution:
Assuming that the stations are independent, the number of active stations can be modeled by a binomial distribution with parameters (10, 0.1). From the formula for p(i), we get
- a.
- b.
- c.
This is shown in Figure 1.3. Note how the probability of one station being active is 0.38, which is greater than the probability of any single station being active. Note also how rapidly the probability of multiple active stations drops. This is what drives spatial statistical multiplexing: the provisioning of a link with a capacity smaller than the sum of the demands of the stations.
){kind=link}
Figure 1.3. Example binomial distribution
1.5.3. Geometric Distribution
Consider a sequence of independent Bernoulli experiments, each of which succeeds with probability a. In section 1.5.2, we wanted to count the number of successes; now, we want to compute the probability mass function of a random variable X that represents the number of trials before the first success. Such a variable is called a geometric random variable and has a probability mass function
The expected value of a geometrically distributed variable with parameter a is 1/a.
Example 1.30. Geometric Random Variable
Assume that a link has a loss probability of 10% and that packet losses are independent, although this is rarely true in practice. Suppose that when a packet gets lost, this is detected and the packet is retransmitted until it is correctly received. What is the probability that it would be transmitted exactly one, two, and three times?
Solution:
Assuming that the packet transmissions are independent events, we note that the probability of success = p = 0.9. Therefore, p(1) = 0.10 * 0.9 = 0.9; p(2) = 0.11 * 0.9 = 0.09; p(3) = 0.12 * 0.9 = 0.009. Note the rapid decrease in the probability of more than two transmissions, even with a fairly high packet loss rate of 10%. Indeed, the expected number of transmissions is only 
.
1.5.4. Poisson Distribution
The Poisson distribution is widely encountered in networking situations, usually to model the arrival of packets or new end-to-end connections to a switch or a router. A discrete random variable X with the domain {0, 1, 2, 3,...} is said to be a Poisson random variable with parameter λ if, for some λ > 0:
Poisson variables are often used to model the number of events that happen in a fixed time interval. If the events are reasonably rare, the probability that multiple events occur in a fixed time interval drops off rapidly, due to the i! term in the denominator. The first use of Poisson variables, indeed, was to investigate the number of soldier deaths due to being kicked by a horse in Napoleon’s army!
The Poisson distribution, which has only a single parameter λ, can be used to model a binomial distribution with two parameters (n and a) when n is “large” and a is “small.” In this case, the Poisson variable’s parameter λ corresponds to the product of the two binomial parameters (i.e., λ = nBinomial* aBinomial). Recall that a binomial distribution arises naturally when we conduct independent trials. The Poisson distribution, therefore, arises when the number of such independent trials is large, and the probability of success of each trial is small. The expected value of a Poisson distributed random variable with parameter λ is also λ.
Consider an endpoint sending a packet on a link. We can model the transmission of a packet by the endpoint in a given time interval as a trial as follows: If the source sends a packet in a particular interval, we will call the trial a success; if the source does not send a packet, we will call the trial a failure. When the load generated by each source is light, the probability of success of a trial defined in this manner, which is just the packet transmission probability, is small. Therefore, as the number of endpoints grows, and if we can assume the endpoints to be independent, the sum of their loads will be well modeled by a Poisson random variable. This is heartening because systems subjected to a Poisson load are mathematically tractable, as we will see in our discussion of queueing theory. Unfortunately, over the last two decades, numerous measurements have shown that actual traffic can be far from Poisson. Therefore, this modeling assumption should be used with care and only as a rough approximation to reality.
Example 1.31. Poisson Random Variable
Consider a link that can receive traffic from one of 1,000 independent endpoints. Suppose that each node transmits at a uniform rate of 0.001 packets/second. What is the probability that we see at least one packet on the link during an arbitrary 1-second interval?
Solution:
Given that each node transmits packets at the rate of 0.001 packets/second, the probability that a node transmits a packet in any 1-second interval is pBinomial = 0.001. Thus, the Poisson parameter λ = 1000*0.001 = 1. The probability that we see at least one packet on the link during any 1-second interval is therefore
That is, there is a 64% chance that, during an arbitrary 1-second interval, we will see one or more packets on the link.
It turns out that a Poisson random variable is a good approximation to a binomial random variable even if the trials are weakly dependent. Indeed, we do not even require the trials to have equal probabilities, as long as the probability of success of each individual trial is “small.” This is another reason why the Poisson random variable is frequently used to model the behavior of aggregates.
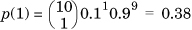
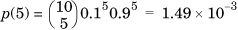
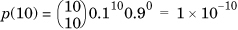
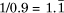