1.4. Moments and Moment Generating Functions
Thus far, we have focused on elementary concepts of probability. To get to the next level of understanding, it is necessary to dive into the somewhat complex topic of moment generating functions. The moments of a distribution generalize its mean and variance. In this section, we will see how we can use a moment generating function (MGF) to compactly represent all the moments of a distribution. The moment generating function is interesting not only because it allows us to prove some useful results, such as the central limit theorem but also because it is similar in form to the Fourier and Laplace transforms, discussed in Chapter 5.
1.4.1. Moments
The moments of a distribution are a set of parameters that summarize it. Given a random variable X, its first moment about the origin, denoted 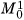 , is defined to be E[X]. Its second moment about the origin, denoted
, is defined to be E[X]. Its second moment about the origin, denoted 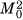 , is defined as the expected value of the random variable X2, or E[X2]. In general, the rth moment of X about the origin, denoted
, is defined as the expected value of the random variable X2, or E[X2]. In general, the rth moment of X about the origin, denoted 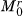 , is defined as
, is defined as 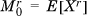 .
.
We can similarly define the rth moment about the mean, denoted 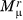 , by E[(X – μ)r]. Note that the variance of the distribution, denoted by σ2, or V[X], is the same as
, by E[(X – μ)r]. Note that the variance of the distribution, denoted by σ2, or V[X], is the same as 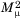 . The third moment about the mean,
. The third moment about the mean, 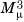 , is used to construct a measure of skewness, which describes whether the probability mass is more to the left or the right of the mean, compared to a normal distribution. The fourth moment about the mean,
, is used to construct a measure of skewness, which describes whether the probability mass is more to the left or the right of the mean, compared to a normal distribution. The fourth moment about the mean, 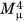 , is used to construct a measure of peakedness, or kurtosis, which measures the “width” of a distribution.
, is used to construct a measure of peakedness, or kurtosis, which measures the “width” of a distribution.
The two definitions of a moment are related. For example, we have already seen that the variance of X, denoted V[X], can be computed as V[X] = E[X2] – (E[X])2. Therefore, 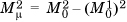 . Similar relationships can be found between the higher moments by writing out the terms of the binomial expansion of (X – μ)r.
. Similar relationships can be found between the higher moments by writing out the terms of the binomial expansion of (X – μ)r.
1.4.2. Moment Generating Functions
Except under some pathological conditions, a distribution can be thought to be uniquely represented by its moments. That is, if two distributions have the same moments, they will be identical except under some rather unusual circumstances. Therefore, it is convenient to have an expression, or “fingerprint,” that compactly represents all the moments of a distribution. Such an expression should have terms corresponding to 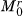 for all values of r.
for all values of r.
We can get a hint regarding a suitable representation from the expansion of ex:

We see that there is one term for each power of x. This suggests the definition of the moment generating function of a random variable X as the expected value of etX, where t is an auxiliary variable:

To see how this represents the moments of a distribution, we expand M(t) as
Thus, the MGF represents all the moments of the random variable X in a single compact expression. Note that the MGF of a distribution is undefined if one or more of its moments are infinite.
We can extract all the moments of the distribution from the MGF as follows: If we differentiate M(t) once, the only term that is not multiplied by t or a power of t is 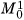 . So,
. So, 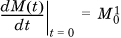 . Similarly,
. Similarly, 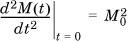 . Generalizing, it is easy to show that to get the rth moment of a random variable X about the origin, we need to differentiate only its MGF r times with respect to t and then set t to 0.
. Generalizing, it is easy to show that to get the rth moment of a random variable X about the origin, we need to differentiate only its MGF r times with respect to t and then set t to 0.
It is important to remember that the “true” form of the MGF is the series expansion in Equation 1.25. The exponential is merely a convenient representation that has the property that operations on the series (as a whole) result in corresponding operations being carried out in the compact form. For example, it can be shown that the series resulting from the product of
This simplifies the computation of operations on the series. However, it is sometimes necessary to revert to the series representation for certain operations. In particular, if the compact notation of M(t) is not differentiable at t = 0, we must revert to the series to evaluate M(0), as shown next.
1.4.3. Properties of Moment Generating Functions
We now prove two useful properties of MGFs.
First, if X and Y are two independent random variables, the MGF of their sum is the product of their MGFs. If their individual MGFs are M1(t) and M2(t), respectively, the MGF of their sum is
Second, if random variable X has MGF M(t), the MGF of random variable Y = a+bX is eatM(bt) because
As a corollary, if M(t) is the MGF of a random variable X, the MGF of (X – μ) is given by e−μtM(t). The moments about the origin of (X – μ) are the moments about the mean of X. So, to compute the rth moment about the mean for a random variable X, we can differentiate e−μtM(t) r times with respect to t and set t to 0.
These two properties allow us to compute the MGF of a complex random variable that can be decomposed into the linear combination of simpler variables. In particular, it allows us to compute the MGF of independent, identically distributed (i.i.d.) random variables, a situation that arises frequently in practice.
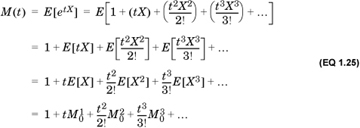
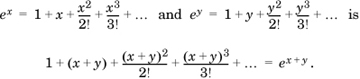
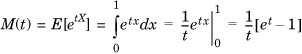 . However, this function is not defined—and therefore not differentiable—at t = 0. Instead, we revert to the series:
. However, this function is not defined—and therefore not differentiable—at t = 0. Instead, we revert to the series: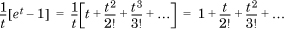
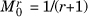 . So,
. So, 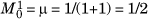 is the mean, and
is the mean, and 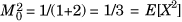 . Note that we found the expression for M(t) by using the compact notation, but reverted to the series for differentiating it. The justification is that the integral of the compact form is identical to the summation of the integrals of the individual terms.
. Note that we found the expression for M(t) by using the compact notation, but reverted to the series for differentiating it. The justification is that the integral of the compact form is identical to the summation of the integrals of the individual terms.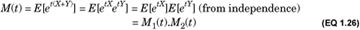
 , so the MGF of random variable X defined as the sum of two independent uniform variables is
, so the MGF of random variable X defined as the sum of two independent uniform variables is 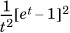 .
.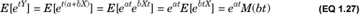
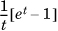 . So, the MGF of (X – μ) is given by
. So, the MGF of (X – μ) is given by 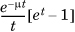 . To find the variance of a standard uniform random variable, we need to differentiate twice with respect to t and then set t to 0. Given the t in the denominator, it is convenient to rewrite the expression as
. To find the variance of a standard uniform random variable, we need to differentiate twice with respect to t and then set t to 0. Given the t in the denominator, it is convenient to rewrite the expression as 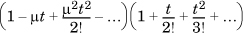 , where the ellipses refer to terms with third and higher powers of t, which will reduce to 0 when t is set to 0. In this product, we need consider only the coefficient of t2, which is
, where the ellipses refer to terms with third and higher powers of t, which will reduce to 0 when t is set to 0. In this product, we need consider only the coefficient of t2, which is 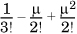 . Differentiating the expression twice results in multiplying the coefficient by 2, and when we set t to zero, we obtain E[(X – μ)2] = V[X] = 1/12.
. Differentiating the expression twice results in multiplying the coefficient by 2, and when we set t to zero, we obtain E[(X – μ)2] = V[X] = 1/12.