1.4 Basic Concepts
The System
A system is that portion of the universe which we have chosen to study.
A closed system is one in which no mass crosses the system boundaries.
An open system is one in which mass crosses the system boundaries. The system may gain or lose mass or simply have some mass pass through it.
An isolated system is one devoid of interactions of any kind with the surroundings (including mass exchange, heat, and work interactions).
System boundaries are established at the beginning of a problem, and simplification of balance equations depends on whether the system is open or closed. Therefore, the system boundaries should be clearly identified. If the system boundaries are changed, the simplification of the mass and energy balance equations should be performed again, because different balance terms are likely to be necessary. These guidelines become more apparent in Chapter 2. In many textbooks, especially those dealing with fluid mechanics, the system is called the control volume. The two terms are synonymous.
Equilibrium
A system is in equilibrium when there is no driving force for a change of intensive variables within the system. The system is "relaxed" relative to all forces and potentials.6
An isolated system moves spontaneously to an equilibrium state. In the equilibrium state there are no longer any driving forces for spontaneous change of intensive variables.
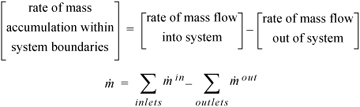
The Mass Balance
Presumably, students in this course are familiar with mass balances from an introductory course in material and energy balances. The relevant relation is simply:
Equation 1.9
where 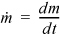 .
. 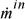 and
and 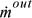 are the absolute values of mass flow rates entering and leaving, respectively.
are the absolute values of mass flow rates entering and leaving, respectively.
We may also write
Equation 1.10
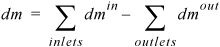
where mass differentials dmin and dmout are always positive. When all the flows of mass are analyzed in detail for several subsystems coupled together, this simple equation may not seem to fully portray the complexity of the application. The general study of thermodynamics is similar in that regard. A number of simple relations like this one are coupled together in a way that requires some training to understand. In the absence of chemical reactions, we may also write a mole balance by replacing mass with moles in the balance.
Heat – Sinks and Reservoirs
Heat is energy in transit between the source from which the energy is coming and a destination toward which the energy is going. When developing thermodynamic concepts, we frequently assume that our system transfers heat to/from a reservoir or sink. A heat reservoir is an infinitely large source or destination of heat transfer. The reservoir is assumed to be so large that the heat transfer does not affect the temperature of the reservoir. A sink is a special name sometimes used for a reservoir which can accept heat without a change in temperature. The assumption of constant temperature makes it easier to concentrate on the thermodynamic behavior of the system while making a reasonable assumption about the part of the universe assigned to be the reservoir.
The mechanics of heat transfer are also easy to picture conceptually from the molecular kinetics perspective. In heat conduction, faster-moving molecules collide with slower ones, exchanging kinetic energy and equilibrating the temperatures. In this manner, we can imagine heat being transferred from the hot surface to the center of a pizza in an oven until the center of the pizza is cooked. In heat convection, packets of hot mass are circulated and mixed, accelerating the equilibration process. Heat convection is important in getting the heat from the oven flame to the surface of the pizza. Heat radiation, the remaining mode of heat transfer, occurs by an entirely different mechanism having to do with waves of electromagnetic energy emitted from a hot body that are absorbed by a cooler body. Radiative heat transfer is typically discussed in detail during courses devoted to heat transfer.
Work
Work is a familiar term from physics. We know that work is a force acting through a distance. There are several ways forces may interact with the system which all fit under this category, including pumps, turbines, agitators, and pistons/cylinders. We will discuss the details of how we calculate work and determine its impact on the system in the next chapter.
Density
Density is a measure of the quantity per unit volume and may be expressed on a molar basis (molar density) or a mass basis (mass density). In some situations, it is expressed as the number of particles per unit volume (number density).
Intensive Properties
Intensive properties are those properties which are independent of the size of the system. For example, in a system at equilibrium without internal rigid/insulating walls, the temperature and pressure are uniform throughout the system and are therefore intensive properties. Specific properties are the total property divided by the mass and are intensive. For example, the molar volume ([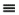 ] length3/mole), mass density ([
] length3/mole), mass density ([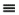 ] mass/length3), and specific internal energy ([
] mass/length3), and specific internal energy ([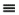 ] energy/mass) are intensive properties. In this text, intensive properties are not underlined.
] energy/mass) are intensive properties. In this text, intensive properties are not underlined.
Extensive Properties
Extensive properties depend on the size of the system, for example the volume ([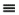 ] length3) and energy ([
] length3) and energy ([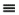 ] energy). Extensive properties are underlined; for example, U = nU, where n is the number of moles and U is molar internal energy.
] energy). Extensive properties are underlined; for example, U = nU, where n is the number of moles and U is molar internal energy.
States and State Properties – The Phase Rule
Two state variables are necessary to specify the state of a single-phase pure fluid, that is, two from the set P, V, T, U. Other state variables to be defined later in the text which also fit in this category are molar enthalpy, molar entropy, molar Helmholtz energy, and molar Gibbs energy. State variables must be intensive properties. As an example, specifying P and T permits you to find the specific internal energy and specific volume of steam. Note, however, that you need to specify only one variable, the temperature or the pressure, if you want to find the properties of saturated vapor or liquid. This reduction in the needed specifications is referred to as a reduction in the "degrees of freedom." As another example in a ternary, two-phase system, the temperature and the mole fractions of two of the components of the lower phase are state variables (the third component is implicit in summing the mole fractions to unity), but the total number of moles of a certain component is not a state variable because it is extensive. In this example, the pressure and mole fractions of the upper phase may be calculated once the temperature and lower-phase mole fractions have been specified. The number of state variables needed to completely specify the state of a system is given by the Gibbs phase rule for a non-reactive system,7:
Equation 1.11
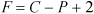
where F is the number of state variables that can be varied while P phases exist in a system where C is the number of components (F is also known as the number of degrees of freedom). More details on the Gibbs phase rule are given in Chapter 16.
Steady-State Open Systems
The term steady state is used to refer to open systems in which the inlet and outlet mass flow rates are invariant with time and there is no mass accumulation. In addition, steady state requires that state variables at all locations are invariant with respect to time. Note that state variables may vary with position. Steady state does not require the system to be at equilibrium. For example, in a heat exchanger operating at steady state with a hot and cold stream, each stream has a temperature gradient along its length, and there is always a driving force for heat transfer from the hotter stream to the colder stream. Section 2.13 describes this process in more detail.
The Ideal Gas Law
The ideal gas is a "model" fluid where the molecules have no attractive potential energy and no size (and thus, no repulsive potential energy). Properties of the ideal gas are calculated from the ideal gas model:
Equation (ig) 1.12
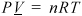
Note that scientists who first developed this formula empirically termed it a "law" and the name has persisted, but it should be more appropriately considered a "model." In the terminology we develop, it is also an equation of state, relating the P-V-T properties of the ideal gas law to one another as shown in Eqn. 1.12 and Fig. 1.3. We know that real molecules have potential energy of attraction and repulsion. Due to the lack of repulsive forces, ideal gas particles can "pass through" one another. Ideal gas molecules are sometimes called "point masses" to communicate this behavior. While the assumptions may seem extreme, we know experimentally that the ideal gas model represents many compounds, such as air, nitrogen, oxygen, and even water vapor at temperatures and pressures near ambient conditions. Use of this model simplifies calculations while the concepts of the energy and entropy balances are developed throughout Unit I. This does not imply that the ideal gas model is applicable to all vapors at all conditions, even for air, oxygen, and nitrogen. Analysis using more complex fluid models is delayed until Unit II. We rely on thermodynamic charts and tables until Unit II to obtain properties for gases that may not be considered ideal gases.
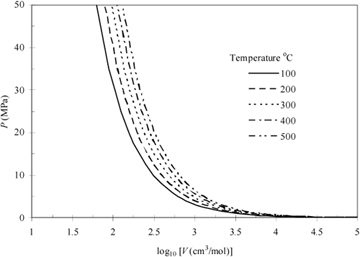
Figure 1.3 Ideal gas behavior at five temperatures.
Because kinetic energy is the only form of energy for an ideal gas, the internal energy of a monatomic ideal gas is given by summing the kinetic energy of the atoms and then relating this to temperature (c.f. Eqn. 1.1):
Equation (ig) 1.13
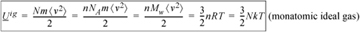
The proportionality constant between temperature and internal energy is known as the ideal gas heat capacity at constant volume, denoted CV. Eqn 1.13 shows that CV = 1.5R for a monatomic ideal gas. If you refer to the tables of constant pressure heat capacities (CP) on the back flap of the text and note that CP = CV + R for an ideal gas, you may be surprised by how accurate this ultrasimplified theory actually is for species like helium, neon, and argon at 298 K.8
While the equality in Eqn. 1.13 is valid for monatomic fluids only, the functionality Uig = Uig(T ) is universal for all ideal gases. For more multi-atom molecules, the heat capacity depends on temperature because vibrations hold some energy in a manner that depends on temperature. However, the observation that Uig = Uig(T ) is true for any ideal gas, not only for ultrasimplified, monatomic ideal gases. We build on this relation in Chapters 6–8, where we show how to compute changes in energy for any fluid at any temperature and density by systematically correcting the relatively simple ideal gas result. Let us explore more completely the assumptions of the ideal gas law by investigating the molecular origins of pressure.
Pressure
Pressure is the force exerted per unit area. We will be concerned primarily with the pressure exerted by the molecules of fluids upon the walls of their containers. Briefly, when molecules collide with the container walls, they must change momentum. The change in momentum creates a force on the wall. As temperature increases, the particles have more kinetic energy (and momentum) when they collide, so the pressure increases. We can understand this more fully with an ultra-simplified analysis of kinetic theory as it relates to the ideal gas law.
Suppose we have two hard spherical molecules in a container that are bouncing back and forth with 1D velocity in the x-direction only and not contacting one another. We wish to quantify the forces acting on each wall. Since the particles are colliding only with the walls at A1 and A2 in our idealized motion, these are the only walls we need to consider. Let us assume that particles bounce off the wall with the same speed which they had before striking the wall, but in the opposite direction (a perfectly elastic collision where the wall is perfectly rigid and absorbs no momentum).
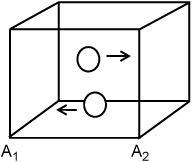
Thus, the kinetic energy of the particles is fixed. If 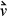 is the initial velocity of the particle (recall that
is the initial velocity of the particle (recall that 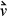 is a vector quantity and notation v represents a scalar) before it strikes a wall, the change in velocity due to striking the wall is –2
is a vector quantity and notation v represents a scalar) before it strikes a wall, the change in velocity due to striking the wall is –2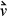 . The change in velocity of the particle indicates the presence of interacting forces between the wall and the particle. If we quantify the force necessary to change the velocity of the particle, we will also quantify the forces of the particle on the wall by Newton's third principle. To quantify the force, we may apply Newton's second principle stated in terms of momentum: The time rate of change of the momentum of a particle is equal to the resultant force acting on the particle and is in the direction of the resultant force.
. The change in velocity of the particle indicates the presence of interacting forces between the wall and the particle. If we quantify the force necessary to change the velocity of the particle, we will also quantify the forces of the particle on the wall by Newton's third principle. To quantify the force, we may apply Newton's second principle stated in terms of momentum: The time rate of change of the momentum of a particle is equal to the resultant force acting on the particle and is in the direction of the resultant force.
Equation 1.14
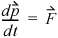
The application of this formula directly is somewhat problematic since the change in direction is instantaneous, and it might seem that the time scale is important. This can be avoided by determining the time-averaged force,9 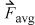 exerted on the wall during time Δt,
exerted on the wall during time Δt,
Equation 1.15
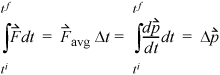
where 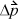 is the total change in momentum during time Δt. The momentum change for each collision is
is the total change in momentum during time Δt. The momentum change for each collision is 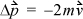 where m is the mass per particle. Collision frequency can be related easily to the velocity. Each particle will collide with the wall every Δt seconds, where Δt = 2 L /v, where L is the distance between A1 and A2. The average force is then
where m is the mass per particle. Collision frequency can be related easily to the velocity. Each particle will collide with the wall every Δt seconds, where Δt = 2 L /v, where L is the distance between A1 and A2. The average force is then
Equation 1.16
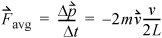
where 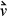 is the velocity before the collision with the wall. Pressure is the force per unit area, and the area of a wall is L2, thus
is the velocity before the collision with the wall. Pressure is the force per unit area, and the area of a wall is L2, thus
Equation (ig) 1.17
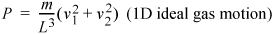
where the subscripts denote the particles. If you are astute, you will recognize L3 as the volume of the box and the kinetic energy which we have shown earlier to relate to the temperature.
If the particle motions are generalized to motion in arbitrary directions, collisions with additional walls in the analysis does not complicate the problem dramatically because each component of the velocity may be evaluated independently. To illustrate, consider a particle bouncing around the centers of four walls in a horizontal plane. From the top view, the trajectory would appear as below:
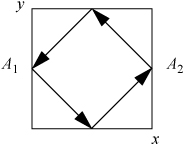
For the same velocity as the first case, the force of each collision would be reduced because the particle strikes merely a glancing blow. The time of collisions between walls is now dependent on the component of velocityperpendicular to the walls. We have chosen a special case to illustrate here, where the box is square and the particle impacts at a 45° angle in the center of each wall. The x-component of the force can be related to the magnitude of the velocity by noting that vx = vy, such that v = (vx2 + vy2)1/2 = vx21/2. The time between collisions with wall A1 would be 4L/(v21/2). The formula for the average force in two dimensions then becomes:
Equation 1.18
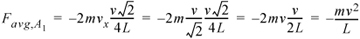
and the pressure due to two particles that do not collide with one another in two dimensions becomes:
Equation (ig) 1.19
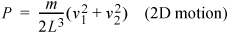
(More complicated impact angles and locations will provide the same results but require more tedious derivations.) The extension to three dimensions is more difficult to visualize, but comparing Eqn. 1.17 to Eqn. 1.19, you should not be surprised to learn that the pressure in three dimensions is:
Equation (ig) 1.20
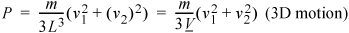
The problem gets more complicated when collisions between particles occur. We ignored that possibility here because the ideal gases being considered are point masses that do not collide with one another. Including molecular collisions is a straightforward implementation of "billiard ball" physics. This subject is discussed further in Section 7.10 on page 276 and with great interactive graphics in the discontinuous molecular dynamics (DMD) module at Etomica.org.
We see a relation developing between P and kinetic energy. When we insert the relation between temperature and kinetic energy (Eqn. 1.1) into Eqn. 1.20 we find that the ideal gas law results for a spherical (monatomic) molecule in 3D,
Equation (ig) 1.21
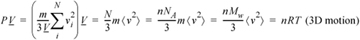
where m is the mass per particle and Mw is the molecular weight. A similar derivation with Eqn. 1.19 gives the results for motions restricted to 2D,10
Equation (ig) 1.22
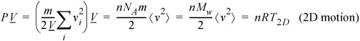
 The placement of system boundaries is a key step in problem solving.
The placement of system boundaries is a key step in problem solving.