Learning the Bridge Pattern: An Example
To help you understand the thinking behind the Bridge pattern and what it is trying to do, I will work through an example from scratch. Starting with requirements, I will derive the pattern and then see how to apply it.
Perhaps this example will seem basic. But look at the concepts discussed in this example and then try to think of situations that you have encountered that are similar, having
- Variations in abstractions of a concept.
- Variations in how these concepts are implemented.
You will see that this example has many similarities to the CAD/CAM problem discussed earlier. Rather than give you all the requirements up front, however, I am going to give them a little at a time, just as they were given to me. You can’t always see the variations at the beginning of the problem.
Bottom line: During requirements definition, explore for variations early and often!
Suppose I have been given the task of writing a program that will draw rectangles with either of two drawing programs. I have been told that when I instantiate a rectangle, I will know whether I should use drawing program 1 (DP1) or drawing program 2 (DP2).
The rectangles are defined as two pairs of points, as represented in Figure 10-1. The differences between the drawing programs are summarized in Table 10-1.
Figure 10-1 Positioning the rectangle.
Table 10-1 Different Drawing Programs
|
|
DP1 |
DP2 |
|
Used to draw a line |
draw_a_line( x1, y1, x2, y2) |
drawline( x1, x2, y1, y2) |
|
Used to draw a circle |
draw_a_circle( x, y, r) |
drawcircle( x, y, r) |
Our analysis specifies that we don’t want the code that draws the rectangles to worry about what type of drawing program it should use. It occurs to me that because the rectangles are told what drawing program to use when instantiated, I can have two different kinds of rectangle objects: one that uses DP1 and one that uses DP2. Each would have a draw method but would implement it differently. Figure 10-2 shows this.
Figure 10-2 Design for rectangles and drawing programs (DP1 and DP2).
By having an abstract class Rectangle, I take advantage of the fact that the only difference between the different types of Rectangles are how they implement the drawLine method. The V1Rectangle is implemented by having a reference to a DP1 object and using that object’s draw_a_line method. The V2Rectangle is implemented by having a reference to a DP2 object and using that object’s drawline method. However, by instantiating the right type of Rectangle, I no longer have to worry about this difference.
Example 10-1 Java Code Fragments
abstract public class Rectangle {
private double _x1, _y1, _x2, _y2;
public Rectangle
(double x1, double y1, double x2, double y2) {
x1= x1; _y1= y1; _x2= x2; _y2= y2;
}
public void draw() {
drawLine( _x1, _y1, _x2, _y1);
drawLine( _x2, _y1, _x2, _y2);
drawLine( _x2, _y2, _x1, _y2);
drawLine( _x1, _y2, _x1, _y1);
}
abstract protected void drawLine
(double x1, double y1, double x2, double y2);
}
Now suppose that after completing this code, one of the inevitable three (death, taxes, and changing requirements) comes my way. I am asked to support another kind of shape—this time, a circle. However, I am also given the mandate that the collection object does not want to know the difference between Rectangles and Circles.
It occurs to me that I can just extend the approach I’ve already started by adding another level to my class hierarchy. I only need to add a new class, called Shape, from which I will derive the Rectangle and Circle classes. This way, the Client object can just refer to Shape objects without worrying about what kind of Shape it has been given.
As a beginning object-oriented analyst, it might seem natural to implement these requirements using only inheritance. For example, I could start out with something like Figure 10-2, and then, for each kind of Shape, implement the shape with each drawing program, deriving a version of DP1 and a version of DP2 for Rectangle and deriving a version of DP1 and a version of DP2 one for Circle. I would end up with Figure 10-3.
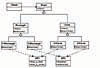
Figure 10-3 A straightforward approach: implementing two shapes and two drawing programs.
I implement the Circle class the same way that I implemented the Rectangle class. However, this time, I implement draw by using drawCircle instead of drawLine.
Example 10-2 Java Code Fragments
abstract class Shape {
abstract public void draw();
}
// the only change to Rectangle is
abstract class Rectangle extends Shape {
//
// V1Rectangle and V2Rectangle don’t change
abstract public class Circle extends Shape {
protected double _x, _y, _r;
public Circle (double x, double y, double r) {
_x= x; _y= y; _r= r;
}
public void draw() {
drawCircle();
}
abstract protected void drawCircle();
}
public class V1Circle extends Circle {
public V1Circle
(double x, double y, double r) {
super(x,y,r);
}
protected void drawCircle () {
DP1.draw_a_circle( _x, _y, _r);
}
}
public class V2Circle extends Circle {
public V2Circle(double x, double y, double r) {
super( x, y, r);
}
protected void drawCircle () {
DP2.drawCircle( _x, _y, _r);
}
}
To understand this design, let’s walk through an example. Consider what the draw method of a V1Rectangle does.
- Rectangle’s draw method is the same as before (calling drawLine four times as needed).
- drawLine is implemented by calling DP1’s draw_a_line.
In action, this looks like Figure 10-4.
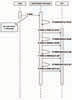
Figure 10-4 Sequence Diagram when have a V1Rectangle.
Even though the class diagram makes it look as if there are many objects, in reality I am only dealing with three objects (see Figure 10-5):
- The Client using the rectangle
- The V1Rectangle object
- The DP1 drawing program
When the Client object sends a message to the V1Rectangle object (called myRectangle) to perform draw, it calls Rectangle’s draw method resulting in Steps 2 through 9.
Figure 10-5 The objects present.
Unfortunately, this approach introduces new problems. Look back at Figure 10-3 and pay attention to the third row of classes. Consider the following:
- The classes in this row represent the four specific types of Shapes that I have.
- What happens if I get another drawing program—that is, another variation in implementation? I will have six different kinds of Shapes (two Shape concepts times three drawing programs).
- Imagine what happens if I then get another type of Shape, another variation in concept. I will have nine different types of Shapes (three Shape concepts times three drawing programs).
The class explosion problem arises because in this solution the abstraction (the kinds of Shapes) and the implementation (the drawing programs) are tightly coupled. Each type of shape must know what type of drawing program it is using. I need a way to separate the variations in abstraction from the variations in implementation so that the number of classes only grows linearly (see Figure 10-6).
Figure 10-6 The Bridge pattern separates variations in abstraction and implementation.
This is exactly the intent of the Bridge pattern: “[to] decouple an abstraction from its implementation so that the two can vary independently.”2
Before showing a solution and deriving the Bridge pattern, I want to mention a few other problems (beyond the combinatorial explosion).
Looking at Figure 10-3, ask yourself what else is poor about this design.
- Does there appear to be redundancy?
- Would you say things have strong cohesion or weak cohesion?
- Are things tightly or loosely coupled?
Would you want to have to maintain this code?
When I first looked at these problems, I thought that part of the difficulty might have been that I simply was using the wrong kind of inheritance hierarchy. Therefore, I tried the alternative hierarchy shown in Figure 10-7.
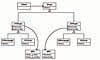
Figure 10-7 An alternative implementation.
I still have the same four classes representing all of my possible combinations. However, by first deriving versions for the different drawing programs, I eliminated the redundancy between the DP1 and DP2 classes.
Unfortunately, I am unable to eliminate the redundancy between the two types of Rectangles and the two types of Circles, each pair of which has the same draw method.
In any event, the class explosion that was present before is still present here.
The sequence diagram for this solution is shown in Figure 10-8.

Figure 10-8 Sequence diagram for new approach.
Although this may be an improvement over the original solution, it still has a problem with scaling. It also still has some of the original cohesion and coupling problems.
Bottom line: I do not want to have to maintain this version either! There must be a better way.
