Information Flow

This chapter is from the book

Introduction to Computer Security

Learn More Buy

This chapter is from the book

This chapter is from the book 

Introduction to Computer Security

Learn More Buy

15.2 Compiler-Based Mechanisms

Compiler-based mechanisms check that information flows throughout a program are authorized. The mechanisms determine if the information flows in a program could violate a given information flow policy. This determination is not precise, in that secure paths of information flow may be marked as violating the policy; but it is secure, in that no unauthorized path along which information may flow will be undetected.

• Definition 15–3. A set of statements is certified with respect to an information flow policy if the information flow within that set of statements does not violate the policy.

if x = 1 then y := a;
else y := b;

15.2.1 Declarations

For our discussion, we assume that the allowed flows are supplied to the checking mechanisms through some external means, such as from a file. The specifications of allowed flows involve security classes of language constructs. The program involves variables, so some language construct must relate variables to security classes. One way is to assign each variable to exactly one security class. We opt for a more liberal approach, in which the language constructs specify the set of classes from which information may flow into the variable. For example,

x: integer class { A, B }

states that x is an integer variable and that data from security classes A and B may flow into x. Note that the classes are statically, not dynamically, assigned. Viewing the security classes as a lattice, this means that x's class must be at least the least upper bound of classes A and B—that is, lub{A, B} ≤ x.

Two distinguished classes, Low and High, represent the greatest lower bound and least upper bound, respectively, of the lattice. All constants are of class Low.

Information can be passed into or out of a procedure through parameters. We classify parameters as input parameters (through which data is passed into the procedure), output parameters (through which data is passed out of the procedure), and input/output parameters (through which data is passed into and out of the procedure).

(* input parameters are named is; output parameters, os; *)
   (* and input/output parameters, ios, with s a subscript *)
   proc something(i1, ..., ik; var o1, ..., om, io1, ..., ion);
   var l1, ..., lj;                (* local variables *)
   begin
   S;                     (* body of procedure *)
   end;
   

The class of an input parameter is simply the class of the actual argument:

• i_s: type class { i_s }

Let r₁, ..., r_p be the set of input and input/output variables from which information flows to the output variable o_s. The declaration for the type must capture this:

• o_s: type class { r₁, ..., r_p }

(We implicitly assume that any output-only parameter is initialized in the procedure.) The input/output parameters are like output parameters, except that the initial value (as input) affects the allowed security classes. Again, let r₁, ..., r_p be defined as above. Then:

• io_s: type class {r₁, ..., r_p, io₁, ..., io_k }

proc sum(x: int class { x };
             var out: int class { x, out });
begin
        out := out + x;
end;

The declarations presented so far deal only with basic types, such as integers, characters, floating point numbers, and so forth. Nonscalar types, such as arrays, records (structures), and variant records (unions) also contain information. The rules for information flow classes for these data types are built on the scalar types.

Consider the array

a: array 1 .. 100 of int;

First, look at information flows out of an element a[i] of the array. In this case, information flows from a[i] and from i, the latter by virtue of the index indicating which element of the array to use. Information flows into a[i] affect only the value in a[i], and so do not affect the information in i. Thus, for information flows from a[i], the class involved is lub{ a[i], i }; for information flows into a[i], the class involved is a[i].

15.2.2 Program Statements

A program consists of several types of statements. Typically, they are

1. Assignment statements

2. Compound statements

3. Conditional statements

4. Iterative statements

5. Goto statements

6. Procedure calls

7. Function calls

8. Input/output statements.

We consider each of these types of statements separately, with two exceptions. Function calls can be modeled as procedure calls by treating the return value of the function as an output parameter of the procedure. Input/output statements can be modeled as assignment statements in which the value is assigned to (or assigned from) a file. Hence, we do not consider function calls and input/output statements separately.

15.2.2.1 Assignment Statements

An assignment statement has the form

y := f(x1, ..., xn)
   

where y and x₁, ..., x_n are variables and f is some function of those variables. Information flows from each of the x_i's to y. Hence, the requirement for the information flow to be secure is

• lub{x₁, ..., x_n} ≤ y

x := y + z;

15.2.2.2 Compound Statements

A compound statement has the form

begin
     S1;
   ...
   Sn;
   end;
   

where each of the S_i's is a statement. If the information flow in each of the statements is secure, then the information flow in the compound statement is secure. Hence, the requirements for the information flow to be secure are

• S₁ secure

• ...

• S_n secure

begin
     x := y + z;
     a := b * c - x;
end;

15.2.2.3 Conditional Statements

A conditional statement has the form

if f(x1, ..., xn) then
   S1;
   else
   S2;
   end;
   

where x₁, . . , x_n are variables and f is some (boolean) function of those variables. Either S₁ or S₂ may be executed, depending on the value of f, so both must be secure. As discussed earlier, the selection of either S₁ or S₂ imparts information about the values of the variables x₁, ..., x_n, so information must be able to flow from those variables to any targets of assignments in S₁ and S₂. This is possible if and only if the lowest class of the targets dominates the highest class of the variables x₁, ..., x_n. Thus, the requirements for the information flow to be secure are

• S₁ secure

• S₂ secure

• lub{x₁, ..., x_n} ≤ glb{ y | y is the target of an assignment in S₁ and S₂ }

As a degenerate case, if statement S₂ is empty, it is trivially secure and has no assignments.

if x + y < z then
     a := b;
else
     d := b * c - x;
end;

15.2.2.4 Iterative Statements

An iterative statement has the form

while f(x1, ..., xn) do
   S;
   

where x₁, ..., x_n are variables and f is some (boolean) function of those variables. Aside from the repetition, this is a conditional statement, so the requirements for information flow to be secure for a conditional statement apply here.

To handle the repetition, first note that the number of repetitions causes information to flow only through assignments to variables in S. The number of repetitions is controlled by the values in the variables x₁, ..., x_n, so information flows from those variables to the targets of assignments in S—but this is detected by the requirements for information flow of conditional statements.

However, if the program never leaves the iterative statement, statements after the loop will never be executed. In this case, information has flowed from the variables x₁, ..., x_n by the absence of execution. Hence, secure information flow also requires that the loop terminate.

Thus, the requirements for the information flow to be secure are

• Iterative statement terminates

• S secure

• lub{x₁, ..., x_n} ≤ glb{ y | y is the target of an assignment in S }

while i < n do
begin
     a[i] := b[i];
     i := i + 1;
end;

15.2.2.5 Goto Statements

A goto statement contains no assignments, so no explicit flows of information occur. Implicit flows may occur; analysis detects these flows.

• Definition 15–4. A basic block is a sequence of statements in a program that has one entry point and one exit point.

proc transmatrix(x: array [1..10][1..10] of int class { x };
             var y: array [1..10][1..10] of int class { y } );
     var i, j: int class { tmp };
begin
    i := 1;                        (* b1 *)
      ________________________________________________________________
      l2: if i > 10 goto l7;             (* b2 *)
      ________________________________________________________________
      j := 1;                        (* b3 *)
      ________________________________________________________________
      l4: if j > 10 then goto l6;        (* b4 *)
      ________________________________________________________________
      y[j][i] := x[i][j];          (* b5 *)
      j := j + 1;
      goto l4;
      ________________________________________________________________
      l6: i := i + 1;                  (* b6 *)
      goto l2;
      ________________________________________________________________
      l7:                              (* b7 *)
      end;
      

Control within a basic block flows from the first line to the last. Analyzing the flow of control within a program is therefore equivalent to analyzing the flow of control among the program's basic blocks. Figure 15-1 shows the flow of control among the basic blocks of the body of the procedure transmatrix.

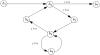Figure 15-1 The control flow graph of the procedure transmatrix. The basic blocks are labeled b1 through b7.The conditions under which branches are taken are shown over the edges corresponding to the branches.

When a basic block has two exit paths, the block reveals information implicitly by the path along which control flows. When these paths converge later in the program, the (implicit) information flow derived from the exit path from the basic block becomes either explicit (through an assignment) or irrelevant. Hence, the class of the expression that causes a particular execution path to be selected affects the required classes of the blocks along the path up to the block at which the divergent paths converge.

• Definition 15–5. An immediate forward dominator of a basic block b (written IFD(b)) is the first block that lies on all paths of execution that pass through b.

Computing the information flow requirement for the set of blocks along the path is now simply applying the logic for the conditional statement. Each block along the path is taken because of the value of an expression. Information flows from the variables of the expression into the set of variables assigned in the blocks. Let B_i be the set of blocks along an execution path from b_i to IFD(b_i), but excluding these endpoints. (See Exercise 3.) Let x_i1, ..., x_in be the set of variables in the expression that selects the execution path containing the blocks in B_i. The requirements for the program's information flows to be secure are

• All statements in each basic block secure

• lub{x_i1, ..., x_in} ≤ glb{ y | y is the target of an assignment in B_i }

15.2.2.6 Procedure Calls

A procedure call has the form

proc procname(i1, ..., im : int; var o1, ..., on : int);
   begin
   S;
   end;
   

where each of the i_j's is an input parameter and each of the o_j's is an input/output parameter. The information flow in the body S must be secure. As discussed earlier, information flow relationships may also exist between the input parameters and the output parameters. If so, these relationships are necessary for S to be secure. The actual parameters (those variables supplied in the call to the procedure) must also satisfy these relationships for the call to be secure. Let x₁, ..., x_m and y₁, ..., y_n be the actual input and input/output parameters, respectively. The requirements for the information flow to be secure are

• S secure

• For j = 1, ..., m and k = 1, ..., n, if i_j ≤ o_k then x_j ≤ y_k

• For j = 1, ..., n and k = 1, ..., n, if o_j ≤ o_k then y_j ≤ y_k

transmatrix(a, b)

15.2.3 Exceptions and Infinite Loops

Exceptions can cause information to flow.

proc copy(x: int class { x }; var y: int class Low);
var  sum: int class { x };
     z: int class Low;
begin
     z := 0;
     sum := 0;
     y := 0;
     while z = 0 do begin
           sum := sum + x;
           y := y + 1;
     end
end

If exceptions are handled explicitly, the compiler can detect problems such as this. Denning again supplies such a solution.

on overflowexception sum do z := 1;

Denning also notes that infinite loops can cause information to flow in unexpected ways.

proc copy(x: int 0..1 class { x };
            var y: int 0..1 class Low);
begin
     y := 0;
     while x = 0 do
          (* nothing *);
     y := 1;
end.

15.2.4 Concurrency

Of the many concurrency control mechanisms that are available, we choose to study information flow using semaphores [270]. Their operation is simple, and they can be used to express many higher-level constructs [135, 718]. The specific semaphore constructs are

wait(x): if x = 0 then block until x > 0; x := x - 1;
signal(x): x := x + 1;

where x is a semaphore. As usual, the wait and the signal are indivisible; once either one has started, no other instruction will execute until the wait or signal finishes.

Reitman and his colleagues [33, 748] point out that concurrent mechanisms add information flows when values common to multiple processes cause specific actions. For example, in the block

begin
     wait(sem);
     x := x + 1;
end;

the program blocks at the wait if sem is 0, and executes the next statement when sem is nonzero. The earlier certification requirement for compound statements is not sufficient because of the implied flow between sem and x. The certification requirements must take flows among local and shared variables (semaphores) into account.

Let the block be

begin
     S1;
   ...
   Sn;
   end;
   

Assume that each of the statements S₁, ..., S_n is certified. Semaphores in the signal do not affect information flow in the program in which the signal occurs, because the signal statement does not block. But following a wait statement, which may block, information implicitly flows from the semaphore in the wait to the targets of successive assignments.

Let statement S_i be a wait statement, and let shared(S_i) be the set of shared variables that are read (so information flows from them). Let g(S_i) be the greatest lower bound of the targets of assignments following S_i. A requirement that the block be secure is that shared(S_i) ≤ g(S_i). Thus, the requirements for certification of a compound statement with concurrent constructs are

• S₁ secure

• ...

• S_n secure

• For i = 1, ..., n [ shared(S_i) ≤ g(S_i) ]

begin
     x := y + z;
     wait(sem);
     a := b * c - x;
end;

Loops are handled similarly. The only difference is in the last requirement, because after completion of one iteration of the loop, control may return to the beginning of the loop. Hence, a semaphore may affect assignments that precede the wait statement in which the semaphore is used. This simplifies the last condition in the compound statement requirement considerably. Information must be able to flow from all shared variables named in the loop to the targets of all assignments. Let shared(S_i) be the set of shared variables read, and let t₁, ..., t_m be the targets of assignments in the loop. Then the certification conditions for the iterative statement

while f(x1, ..., xn) do
   S;
   

are

• Iterative statement terminates

• S secure

• lub{x₁, ..., x_n} ≤ glb{ t₁, ..., t_m }

• lub{shared(S₁), ,,,, shared(S_n) } ≤ glb{ t₁, ..., t_m }

while i < n do
begin
     a[i] := item;
     wait(sem);
     i := i + 1;
end;

Finally, concurrent statements have no information flow among them per se. Any such flows occur because of semaphores and involve compound statements (discussed above). The certification conditions for the concurrent statement

cobegin
     S1;
   ...
   Sn;
   coend;
   

are

• S₁ secure

• ...

• S_n secure

cobegin
     x := y + z;
     a := b * c - y;
coend;

15.2.5 Soundness

Denning and Denning [247], Andrews and Reitman [33], and others build their argument for security on the intuition that combining secure information flows produces a secure information flow, for some security policy. However, they never formally prove this intuition. Volpano, Irvine, and Smith [920] express the semantics of the above-mentioned information on flow analysis as a set of types, and equate certification that a certain flow can occur to the correct use of types. In this context, checking for valid information flows is equivalent to checking that variable and expression types conform to the semantics imposed by the security policy.

Let x and y be two variables in the program. Let x's label dominate y's label. A set of information flow rules is sound if the value in x cannot affect the value in y during the execution of the program. Volpano, Irvine, and Smith use language-based techniques to prove that, given a type system equivalent to the certification rules discussed above, all programs without type errors have the noninterference property described above. Hence, the information flow certification rules of Denning and of Andrews and Reitman are sound.