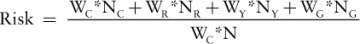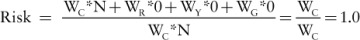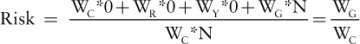Risk Modeling
This chapter presents my techniques for modeling and quantifying risk. These models complement each other in how they measure the risk. You often need more than one model to help you choose between options—no model is ever perfect. However, each of the risk models should yield comparable results.
Risk values are always relative. For example, jumping off a fast-moving train is risky. However, if that train is about to go over a cliff, jumping is the most sensible thing to do. Risk has no absolute value, so you can evaluate it only in comparison with other alternatives. You should therefore talk about a “riskier” project as opposed to a “risky” project. Similarly, nothing is really safe. The only safe way of doing any project is not doing it. You should therefore talk about a “safer” project rather than a “safe” project.
Normalizing Risk
The whole point of evaluating risk is to be able to compare options and projects, which requires comparing numbers. The first decision I made when creating the models was to normalize risk to the numerical range of 0 to 1.
A risk value of 0 does not mean that the project is risk-free. A risk value of 0 means that you have minimized the risk of the project. Similarly, a risk value of 1 does not mean that the project is guaranteed to fail, but simply that you have maximized the risk of the project.
The risk value also does not indicate a probability of success. With probability, a value of 1 means a certainty, and a value of 0 means an impossibility. A project with a risk value of 1 can still deliver, and a project with a risk value of 0 can still fail.
Risk and Floats
The floats of the various activities in the network provide an objective way of measuring the risk of the project, and the previous chapters have referred to floats when discussing risk. Two different project design options will differ in their floats and, therefore, may drastically differ in their risk as well. As an example, consider the two project design options shown in Figure 10-3.
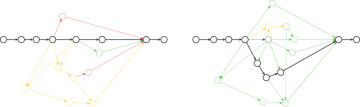
FIGURE 10-3 Two project options
Both of these options are valid project design options for building the same system. The only information available in Figure 10-3 is the color-coded floats of the two networks. Now, ask yourself: With which project would you rather be involved? Everyone to whom I have shown these two charts preferred the greener option on the right-hand side of Figure 10-3. What is interesting is that no one has ever asked what the difference in duration and cost between these two options was. Even when I volunteered that the greener option was both 30% longer and more expensive, that information did not affect the preference. No one chose the low-float, high-stress, and high-risk project shown on the left in Figure 10-3.
Design Risk
Your project faces multiple types of risk. There is staffing risk (Will the project actually gets the level of staffing it requires?). There is duration risk (Will the project be allowed the duration it requires?). There is technological risk (Will the technology be able to deliver?). There are human factors (Is the team technically competent and can they work together?). There is always an execution risk (Can the project manager execute correctly the project plan?).
These types of risk are independent of the kind of risk you assess using floats. Any project design solution always assumes that the organization or the team will have what it takes to deliver on the planned schedule and cost and that the project will receive the required time and resources. The remaining type of risk pertains to how well the project will handle the unforeseen. I call this kind of risk design risk.
Design risk assesses the project’s sensitivity to schedule slips of activities and to your ability to meet your commitments. Design risk therefore quantifies the fragility of the project or the degree to which the project resembles a house of cards. Using floats to measure risk is actually quantifying that design risk.
Risk and Direct Cost
The project risk measurements usually correlate to the direct cost and duration of the various solutions. In most projects, the indirect cost is independent of the project risk. The indirect cost keeps mounting with the duration of the project even if the risk is very low. Therefore, this chapter refers to only direct cost.
Criticality Risk
The criticality risk model attempts to quantify the intuitive impression of risk when you evaluate the options of Figure 10-3. For this risk model you classify activities in the project into four risk categories, from most to least risk:
Critical activities. The critical activities are obviously the riskiest activities because any delay with a critical activity always causes schedule and cost overruns.
High risk activities. Low float, near-critical activities are also risky because any delay in them is likely to cause schedule and cost overruns.
Medium risk activities. Activities with a medium level of float have medium level of risk and can sustain some delays.
Low risk activities. Activities with high floats are the least risky and can sustain even large delays without derailing the project.
You should exclude activities of zero duration (such as milestones and dummies) from this analysis because they add nothing to the risk of the project. Moreover, unlike real activities, they are simply artifacts of the project network.
Chapter 8 showed how to use color coding to classify activities based on their float. You can use the same technique for evaluating the sensitivity or fragility of activities by color coding the four risk categories. With the color coding in place, assign a weight to the criticality of each activity. The weight acts as a risk factor. You are, of course, at liberty to choose any weights that signify the difference in risk. One possible allocation of weights is shown in Table 10-1.
Table 10-1 Criticality risk weights
Activity Color |
Weight |
|---|---|
Black (critical) |
4 |
Red (high risk) |
3 |
Yellow (medium risk) |
2 |
Green (low risk) |
1 |
The criticality risk formula is:
where:
WC is the weight of the black, critical activities.
WR is the weight of red, low-float activities.
WY is the weight of yellow, medium-float activities.
WG is the weight of green, high-float activities.
NC is the number of the black, critical activities.
NR is the number of red, low-float activities.
NY is the number of yellow, medium-float activities.
NG is the number of green, high-float activities.
N is the number of activities in the project (N = NC + NR + NY + NG).
Substituting the weights from Table 10-1, the criticality risk formula is:
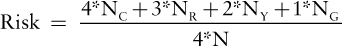
Applying the criticality risk formula to the network in Figure 10-4 yields:
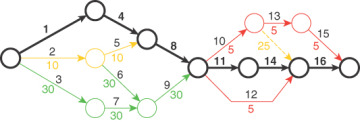
FIGURE 10-4 Sample network for risk calculation
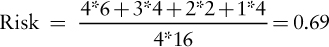
Criticality Risk Values
The maximum value of the criticality risk is 1.0; it occurs when all activities in the network are critical. In such a network, NR, NY, and NG are zero, and NC equals N:
The minimum value of the criticality risk is WG over WC; it occurs when all activities in the network are green. In such a network, NC, NR, and NY are zero, and NG equals N:
Using the weights from Table 10-1, the minimum value of risk is 0.25. The criticality risk, therefore, can never be zero: A weighted average such as this will always have a minimum value greater than zero as long as the weights themselves are greater than zero. This is not necessarily a bad thing, as the project risk should never be zero. The formula implies the lowest range of risk values is too low to achieve, which is reasonable since anything worth doing requires risk.
Choosing Weights
As long as you can rationalize your choice of weights, the criticality risk model will likely work. For example, the set of weights [21, 22, 23, 24] is a poor choice because 21 is only 14% smaller than 24; thus, this set does not emphasize the risk of the green versus the critical activities. Furthermore, the minimum risk using these weights (Wg /Wc) is 0.88, which is obviously too high. I find the weights set [1, 2, 3, 4] to be as good as any other sensible choice.
Customizing Criticality Risk
The criticality risk model often requires some customization and judgment calls. First, as mentioned in Chapter 8, the ranges of the various colors (the criteria for red, yellow, and green activities) must be appropriate for the duration of your project. Second, you should consider defining very-low-float or near-critical activities (such as those with 1 day of float) as critical because these basically have the same risk as critical activities. Third, even if some activities’ floats are not near-critical, you should examine the chain on which the activities reside and adjust it accordingly. For example, if you have a year-long chain of many activities and the chain has only 10 days of float, you should classify each activity on the chain as a critical activity for risk calculation. A slip with one activity up that chain will consume all float, turning all downstream activities into critical activities.