Time–Risk Curve
Just as the project has a time–cost curve, it also has a time–risk curve. The ideal curve is shown in Figure 10-1 by the dashed line.
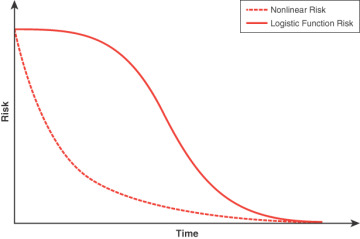
FIGURE 10-1 Ideal time–risk curves
As you compress the project, the shorter project design solutions carry with them an increased level of risk, and the rate of increase is likely nonlinear. This is why the dashed line in Figure 10-1 curves up toward the vertical risk axis and relaxes downward with time. However, this intuitive dashed line is wrong. In reality, a time–risk curve is a logistic function of some kind, the solid line in Figure 10-1.
The logistic function is a superior model because it more closely captures the general behavior of risk in complex systems. For example, if I were to plot the risk of me burning dinner tonight due to compressing the normal preparation time, the risk curve would look like the solid line in Figure 10-1. Each compression technique—such as setting the oven temperature too high, placing the tray too close to the heating element, choosing easier-to-cook but more flammable food, not preheating the oven, and so on—increases the risk of burning dinner. As shown by the solid line, the risk of a burnt dinner due to the cumulative compression at some point is almost maximized and even flattens out, because dinner is certain to burn. Similarly, if I decide not to even enter the kitchen, then the risk would drop precipitously. If the risk was dictated by the dashed line, I would always have some chance of not burning dinner since I could always keep increasing the risk by compressing it further.
Note that the logistic function has a tipping point where the risk drastically increases (the analog to the decision to enter the kitchen). The dashed line, by contrast, keeps increasing gradually and does not have a noticeable tipping point.
Actual Time–Risk Curve
It turns out that even the logistic function in Figure 10-1 is still an idealized time–risk curve. The actual time–risk curve is more like that shown in Figure 10-2. The reason for the shape of this curve is best explained by overlaying it with the project’s direct cost curve. Since the project behavior is three-dimensional, Figure 10-2 relies on a secondary y-axis for the risk.
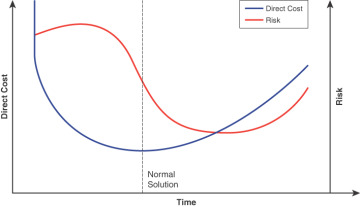
FIGURE 10-2 Actual time–cost–risk curve
The vertical dashed line in Figure 10-2 indicates the duration of the normal solution as well as the minimum direct cost solution for the project. Note that the normal solution usually trades some amount of float to reduce staffing. The reduction in float manifests in an elevated level of risk.
To the left of the normal solution are the shorter, compressed solutions. The compressed solutions are also riskier, so the risk curve increases to the left of the normal solution. The risk rises and then levels off (as is the case with the ideal logistic function). However, unlike the ideal behavior, the actual risk curve gets maximized before the point of minimum duration and even drops a bit, giving it a concave shape. While such behavior is counterintuitive, it occurs because in general, shorter projects are somewhat safer, a phenomenon I call the da Vinci effect. When investigating the tensile strength of wires, Leonardo da Vinci found that shorter wires are stronger than longer wires (it is because the probability of a defect is proportional to the length of the wire).1 In analogy, the same is true for projects. To illustrate the point, consider two possible ways of delivering a 10-man-year project: 1 person for 10 years or 3650 people for 1 day. Assuming both are viable projects (that the people are available, that you have the time, and so on), the 1-day project is much safer than the 10-year project. The likelihood of something bad happening in a single day is open for debate, but it is a near certainty with 10 years. I provide a more quantified explanation for this behavior later in this chapter.
To the right of the normal solution, the risk goes down, at least initially. For example, giving an extra week to a one-year project will reduce the risk of not meeting that commitment. However, if you keep giving the project more time, at some point Parkinson’s law will take effect and drastically increase the risk. So, to the right of the normal solution, the risk curve goes down, becomes minimized at some value greater than zero, and then starts climbing again, giving it a convex shape.
