6.6 Training an A2C Agent
In this section we show how to train an Actor-Critic agent to play Atari Pong using different advantage estimates—first n-step returns, then GAE. Then, we apply A2C with GAE to a continuous-control environment BipedalWalker.
6.6.1 A2C with n-Step Returns on Pong
A spec file which configures an Actor-Critic agent with n-step returns advantage estimate is shown in Code 6.7. The file is available in SLM Lab at slm_lab/spec/benchmark/a2c/a2c_nstep_pong.json.
Code 6.7 A2C with n-step returns: spec file
1 # slm_lab/spec/benchmark/a2c/a2c_nstep_pong.json
2
3 {
4 "a2c_nstep_pong": {
5 "agent": [{
6 "name": "A2C",
7 "algorithm": {
8 "name": "ActorCritic",
9 "action_pdtype": "default",
10 "action_policy": "default",
11 "explore_var_spec": null,
12 "gamma": 0.99,
13 "lam": null,
14 "num_step_returns": 11,
15 "entropy_coef_spec": {
16 "name": "no_decay",
17 "start_val": 0.01,
18 "end_val": 0.01,
19 "start_step": 0,
20 "end_step": 0
21 },
22 "val_loss_coef": 0.5,
23 "training_frequency": 5
24 },
25 "memory": {
26 "name": "OnPolicyBatchReplay"
27 },
28 "net": {
29 "type": "ConvNet",
30 "shared": true,
31 "conv_hid_layers": [
32 [32, 8, 4, 0, 1],
33 [64, 4, 2, 0, 1],
34 [32, 3, 1, 0, 1]
35 ],
36 "fc_hid_layers": [512],
37 "hid_layers_activation": "relu",
38 "init_fn": "orthogonal_",
39 "normalize": true,
40 "batch_norm": false,
41 "clip_grad_val": 0.5,
42 "use_same_optim": false,
43 "loss_spec": {
44 "name": "MSELoss"
45 },
46 "actor_optim_spec": {
47 "name": "RMSprop",
48 "lr": 7e-4,
49 "alpha": 0.99,
50 "eps": 1e-5
51 },
52 "critic_optim_spec": {
53 "name": "RMSprop",
54 "lr": 7e-4,
55 "alpha": 0.99,
56 "eps": 1e-5
57 },
58 "lr_scheduler_spec": null,
59 "gpu": true
60 }
61 }],
62 "env": [{
63 "name": "PongNoFrameskip-v4",
64 "frame_op": "concat",
65 "frame_op_len": 4,
66 "reward_scale": "sign",
67 "num_envs": 16,
68 "max_t": null,
69 "max_frame": 1e7
70 }],
71 "body": {
72 "product": "outer",
73 "num": 1,
74 },
75 "meta": {
76 "distributed": false,
77 "log_frequency": 10000,
78 "eval_frequency": 10000,
79 "max_session": 4,
80 "max_trial": 1
81 }
82 }
83 }
Let’s walk through the main components.
Algorithm: The algorithm is Actor-Critic (line 8), the action policy is the default policy (line 10) for discrete action space (categorical distribution). γ is set on line 12. If lam is specified for λ (not null), then GAE is used to estimate the advantages. If num_step_returns is specified instead, then n-step returns is used (lines 13–14). The entropy coefficient and its decay during training is specified in lines 15–21. The value loss coefficient is specified in line 22.
Network architecture: Convolutional neural network with three convolutional layers and one fully connected layer with ReLU activation function (lines 29–37). The actor and critic use a shared network as specified in line 30. The network is trained on a GPU if available (line 59).
Optimizer: The optimizer is RMSprop [50] with a learning rate of 0.0007 (lines 46–51). If separate networks are used instead, it is possible to specify a different optimizer setting for the critic network (lines 52–57) by setting use_same_optim to false (line 42). Since the network is shared in this case, this is not used. There is no learning rate decay (line 58).
Training frequency: Training is batch-wise because we have selected OnPolicyBatchReplay memory (line 26) and the batch size is 5 × 16. This is controlled by the training_frequency (line 23) and the number of parallel environments (line 67). Parallel environments are discussed in Chapter 8.
Environment: The environment is Atari Pong [14, 18] (line 63).
Training length: Training consists of 10 million time steps (line 69).
Evaluation: The agent is evaluated every 10,000 time steps (line 78).
To train this Actor-Critic agent using SLM Lab, run the commands shown in Code 6.8 in a terminal. The agent should start with the score of -21 and achieve close to the maximum score of 21 on average after 2 million frames.
Code 6.8 A2C with n-step returns: training an agent
1 conda activate lab
2 python run_lab.py slm_lab/spec/benchmark/a2c/a2c_nstep_pong.json
↪ a2c_nstep_pong train
This will run a training Trial with four Sessions to obtain an average result. The trial should take about half a day to complete when running on a GPU. The graph and its moving average are shown in Figure 6.2.
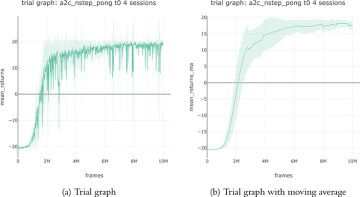
FIGURE 6.2 Actor-Critic (with n-step returns) trial graphs from SLM Lab averaged over four sessions. The vertical axis shows the total rewards averaged over eight episodes during checkpoints, and the horizontal axis shows the total training frames. A moving average with a window of 100 evaluation checkpoints is shown on the right.
6.6.2 A2C with GAE on Pong
Next, to switch from n-step returns to GAE, simply modify the spec from Code 6.7 to specify a value for lam and set num_step_returns to null, as shown in Code 6.9. The file is also available in SLM Lab at slm_lab/spec/benchmark/a2c/a2c_gae_pong.json.
Code 6.9 A2C with GAE: spec file
1 # slm_lab/spec/benchmark/a2c/a2c_gae_pong.json
2
3 {
4 "a2c_gae_pong": {
5 "agent": [{
6 "name": "A2C",
7 "algorithm": {
8 ...
9 "lam": 0.95,
10 "num_step_returns": null,
11 ...
12 }
13 }
Then, run the commands shown in Code 6.10 in a terminal to train an agent.
Code 6.10 A2C with GAE: training an agent
1 conda activate lab 2 python run_lab.py slm_lab/spec/benchmark/a2c/a2c_gae_pong.json a2c_gae_pong ↪ train
Similarly, this will run a training Trial to produce the graphs shown in Figure 6.3.
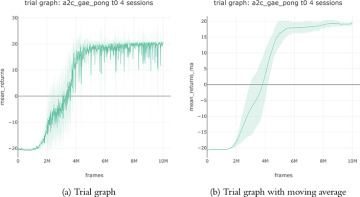
FIGURE 6.3 Actor-Critic (with GAE) trial graphs from SLM Lab averaged over four sessions.
6.6.3 A2C with n-Step Returns on BipedalWalker
So far, we have been training on discrete environments. Recall that policy-based method can also be applied directly to continuous-control problems. Now we will look at the BipedalWalker environment that was introduced in Section 1.1.
Code 6.11 shows a spec file which configures an A2C with n-step returns agent for the BipedalWalker environment. The file is available in SLM Lab at slm_lab/spec/benchmark/a2c/a2c_nstep_cont.json. In particular, note the changes in network architecture (lines 29–31) and environment (lines 54–57).
Code 6.11 A2C with n-step returns on BipedalWalker: spec file
1 # slm_lab/spec/benchmark/a2c/a2c_nstep_cont.json
2
3 {
4 "a2c_nstep_bipedalwalker": {
5 "agent": [{
6 "name": "A2C",
7 "algorithm": {
8 "name": "ActorCritic",
9 "action_pdtype": "default",
10 "action_policy": "default",
11 "explore_var_spec": null,
12 "gamma": 0.99,
13 "lam": null,
14 "num_step_returns": 5,
15 "entropy_coef_spec": {
16 "name": "no_decay",
17 "start_val": 0.01,
18 "end_val": 0.01,
19 "start_step": 0,
20 "end_step": 0
21 },
22 "val_loss_coef": 0.5,
23 "training_frequency": 256
24 },
25 "memory": {
26 "name": "OnPolicyBatchReplay",
27 },
28 "net": {
29 "type": "MLPNet",
30 "shared": false,
31 "hid_layers": [256, 128],
32 "hid_layers_activation": "relu",
33 "init_fn": "orthogonal_",
34 "normalize": true,
35 "batch_norm": false,
36 "clip_grad_val": 0.5,
37 "use_same_optim": false,
38 "loss_spec": {
39 "name": "MSELoss"
40 },
41 "actor_optim_spec": {
42 "name": "Adam",
43 "lr": 3e-4,
44 },
45 "critic_optim_spec": {
46 "name": "Adam",
47 "lr": 3e-4,
48 },
49 "lr_scheduler_spec": null,
50 "gpu": false
51 }
52 }],
53 "env": [{
54 "name": "BipedalWalker-v2",
55 "num_envs": 32,
56 "max_t": null,
57 "max_frame": 4e6
58 }],
59 "body": {
60 "product": "outer",
61 "num": 1
62 },
63 "meta": {
64 "distributed": false,
65 "log_frequency": 10000,
66 "eval_frequency": 10000,
67 "max_session": 4,
68 "max_trial": 1
69 }
70 }
71 }
Run the commands shown in Code 6.12 in a terminal to train an agent.
Code 6.12 A2C with n-step returns on BipedalWalker: training an agent
1 conda activate lab 2 python run_lab.py slm_lab/spec/benchmark/a2c/a2c_nstep_cont.json ↪ a2c_nstep_bipedalwalker train
This will run a training Trial to produce the graphs shown in Figure 6.4.
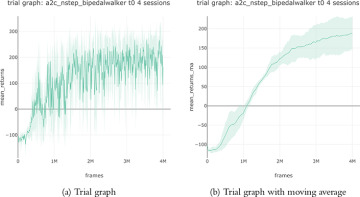
FIGURE 6.4 Trial graphs of A2C with n-step returns on BipedalWalker from SLM Lab averaged over four sessions.
BipedalWalker is a challenging continuous environment that is considered solved when the total reward moving average is above 300. In Figure 6.4, our agent did not achieve this within 4 million frames. We will return to this problem in Chapter 7 with a better attempt.
