13.2 Experiments
The case that might be familiar to you is an AB test. You can make a change to a product and test it against the original version of the product. You do this by randomly splitting your users into two groups. The group membership is denoted by D, where D = 1 is the group that experiences the new change (the test group), and D = 0 is the group that experiences the original version of the product (the control group). For concreteness, let’s say you’re looking at the effect of a recommender system change that recommends articles on a website. The control group experiences the original algorithm, and the test group experiences the new version. You want to see the effect of this change on total pageviews, Y.
You’ll measure this effect by looking at a quantity called the average treatment effect (ATE). The ATE is the average difference in the outcome between the test and control groups, Etest[Y]− Econtrol[Y], or δnaive = E[Y|D = 1]− E[Y|D = 0]. This is the “naive” estimator for the ATE since here we’re ignoring everything else in the world. For experiments, it’s an unbiased estimate for the true effect.
A nice way to estimate this is to do a regression. That lets you also measure error bars at the same time and include other covariates that you think might reduce the noise in Y so you can get more precise results. Let’s continue with this example.
1 import numpy as np
2 import pandas as pd
3
4 N = 1000
5
6 x = np.random.normal(size=N)
7 d = np.random.binomial(1., 0.5, size=N)
8 y = 3. * d + x + np.random.normal()
9
10 X = pd.DataFrame({'X': x, 'D': d, 'Y': y})
Here, we’ve randomized D to get about half in the test group and half in the control. X is some other covariate that causes Y, and Y is the outcome variable. We’ve added a little extra noise to Y to just make the problem a little noisier.
You can use a regression model Y = β0 + β1D to estimate the expected value of Y, given the covariate D, as E[Y|D] = β0 + β1D. The β0 piece will be added to E[Y|D] for all values of D (i.e., 0 or 1). The β1 part is added only when D = 1 because when D = 0, it’s multiplied by zero. That means E[Y|D = 0] = β0 when D = 0 and E[Y|D = 1] = β0 + β1 when D = 1. Thus, the β1 coefficient is going to be the difference in average Y values between the D = 1 group and the D = 0 group, E[Y|D = 1]− E[Y|D = 0] = β1! You can use that coefficient to estimate the effect of this experiment.
When you do the regression of Y against D, you get the result in Figure 13.1.
1 from statsmodels.api import OLS 2 X['intercept'] = 1. 3 model = OLS(X['Y'], X[['D', 'intercept']]) 4 result = model.fit() 5 result.summary()
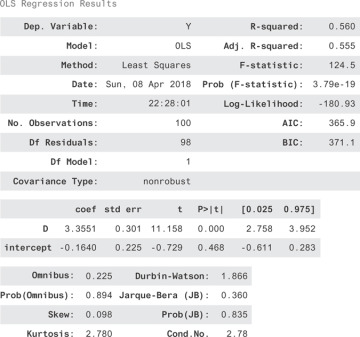
Figure 13.1 The regression for Y = ͎0 + β1D
Why did this work? Why is it okay to say the effect of the experiment is just the difference between the test and control group outcomes? It seems obvious, but that intuition will break down in the next section. Let’s make sure you understand it deeply before moving on.
Each person can be assigned to the test group or the control group, but not both. For a person assigned to the test group, you can talk hypothetically about the value their outcome would have had, had they been assigned to the control group. You can call this value Y0 because it’s the value Y would take if D had been set to 0. Likewise, for control group members, you can talk about a hypothetical Y1. What you really want to measure is the difference in outcomes δ = Y1− Y0 for each person. This is impossible since each person can be in only one group! For this reason, these Y1 and Y0 variables are called potential outcomes.
If a person is assigned to the test group, you measure the outcome Y = Y1. If a person is assigned to the control group, you measure Y = Y0. Since you can’t measure the individual effects, maybe you can measure population level effects. We can try to talk instead about E[Y1] and E[Y0]. We’d like E[Y1] = E[Y|D = 1] and E[Y0] = E[Y|D = 0], but we’re not guaranteed that that’s true. In the recommender system test example, what would happen if you assigned people with higher Y0 pageview counts to the test group? You might measure an effect that’s larger than the true effect!
Fortunately, you randomize D to make sure it’s independent of Y0 and Y1. That way, you’re sure that E[Y1] = E[Y|D = 1] and E[Y0] = E[Y|D = 0], so you can say that = E[Y1− Y0] = E[Y|D = 1]− E[Y|D = 0]. When other factors can influence assignment, D, then you can no longer be sure you have correct estimates! This is true in general when you don’t have control over a system, so you can’t ensure D is independent of all other factors.
In the general case, D won’t just be a binary variable. It can be ordered, discrete, or continuous. You might wonder about the effect of the length of an article on the share rate, about smoking on the probability of getting lung cancer, of the city you’re born in on future earnings, and so on.
Just for fun before we go on, let’s see something nice you can do in an experiment to get more precise results. Since we have a co-variate, X, that also causes Y, we can account for more of the variation in Y. That makes our predictions less noisy, so our estimates for the effect of D will be more precise! Let’s see how this looks. We regress on both D and X now to get Figure 13.2.
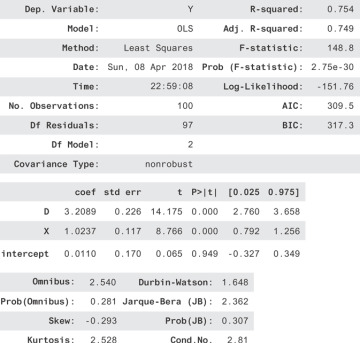
Figure 13.2 The regression for Y = β0 + β1D + β2X
Notice that the R2 is much better. Also, notice that the confidence interval for D is much narrower! We went from a range of 3.95− 2.51 = 1.2 down to 3.65− 2.76 = 0.89. In short, finding covariates that account for the outcome can increase the precision of your experiments!
