- 1.1 What Is Mass Transfer?
- 1.2 Preliminaries: Continuum and Concentration
- 1.3 Flux Vector
- 1.4 Concentration Jump at Interface
- 1.5 Application Examples
- 1.6 Basic Methodology of Model Development
- 1.7 Conservation Principle
- 1.8 Differential Models
- 1.9 Macroscopic Scale
- 1.10 Mesoscopic or Cross-Section Averaged Models
- 1.11 Compartmental Models
- Summary
- Review Questions
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.2 Preliminaries: Continuum and Concentration
The modeling of mass transfer process primarily involves the computation of the concentration profile and the rate at which species A, B, C, and so on are transported across any surface in the media. The intrinsic rate of transport (the transport rate per unit area) is quantified in terms of the flux vector, and this section introduces the preliminaries. The notion of the flux vector is then discussed in Section 1.3.
1.2.1 The Continuum Assumption
The key concept in transport modeling is the continuum assumption, which states that matter is distributed continuously in space. Thus we address the bulk properties rather than the molecular-level interactions. The continuum concept permits us to assign local values to variables at each and every point in an Euclidean space. We can then speak of a temperature field, concentration field, velocity field, and so on.
1.2.2 Concentration: Mole Units
In the context of the continuum approximation, the local concentration, CA may be defined as
where V is the volume element and MA is the moles of species A present in that volume. In this book, the S.I. system of units is used, with kg, m, and s being the basic units. However, the basic unit of concentration, is mol/m3, where mol refers to g mol, rather than kg mol. The molarity, denoted as M, is also often used for concentration; it is equivalent to mol/L. Hence 1 M = 1000 mole/m3—a useful conversion factor. Note that units of kmol/m3 can also be used to represent concentration if convenient. In the final calculations, this will need to be converted to gmol/m3 to maintain consistency of units.
The total molar concentration of the mixture C (at any position and at any time) is defined as the summation of all the species concentrations:
where ns is the total number of species present in the mixture.
The total concentration for a gas mixture CG and the total pressure for an ideal gas mixture are related as
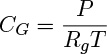
Here Rg is the gas constant, which has a value of 8.314(Pa m3/mol K in the S.I. system of units. Note that the units of Rg can also be expressed as J/mol K.
For example, for a gas at 1 bar pressure and 300 K, the total concentration is calculated as 1 × 105 Pa/[8.314(Pa m3/mol K) × 300 K] and has a value of 37 mol/m3.
Total concentration in liquid can be calculated if the partial molar volume of the components in the mixture solution is known. For dilute solutions, it can be based on the density of the solvent.
For example, for a dilute aqueous solution we can use the density of water as the representative density of the mixture. Hence ρ = 1000 kg/m3. The molecular weight of water is expressed as 18 × 10–3 kg/mol rather than as 18 g/mol. Hence the total concentration in dilute solution can be approximated as 1000 kg/m3/18 × 10–3 kg/mol = 55556 mol/m3.
Very often it is necessary to refer to two or more phases—for example, a gas and a liquid. In such cases we use CAG to represent the concentration of A in the gas phase and CAL to represent the concentration in the liquid. Thus we use the first subscript to represent the species by either by numbers i = 1, 2, . . . or simply by names as A, B, . . . , especially for binary mixtures. The second subscript is used to represent the phase (or the location) where it is present. Similarly, CG rather than C is used for the total concentration in the gas phase and CL for the total concentration in the liquid phase. The ratio of CA to C is called the mole fraction, denoted by yA for gas mixtures or xA for liquid mixtures:
The average molecular weight of the mixture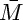 
is calculated as
where MA is the molecular weight of species A. Also note that
where ρ is the density of the mixture.
1.2.3 Concentration: Mass Units
Another way of expressing the species concentration is to use the mass units. The mass concentration (also called the partial density) is designated by ρA and is defined as the mass of species A per unit volume of the mixture locally at a point in the fluid continuum. This quantity is related to CA simply by the species molecular weight:
Note that ρA is the density of A in the mixture (same as mass of A per unit volume of the mixture) and should not be confused with the pure component density of A. The latter will be denoted in this book with a superscript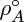 
if we have to refer to both quantities in the same context.
The summation of this for all the species is the mixture density, ρ:
The ratio of ρA to ρ is the mass fraction of species A, denoted often by ωA:
The average molecular weight of the mixture is calculated from the mass fraction values by the reciprocal weighting rule:
1.2.4 Concentration: Partial Pressure Units
In gaseous systems, a measure of concentration is the partial pressure of a species. This follows from the ideal gas law:
or
Partial pressure is therefore a direct measure of concentration in an ideal gas mixture and used commonly for such cases. The partial pressure difference can be used as a driving force for mass transfer instead of concentration differences for (ideal) gas-phase systems. The two sets of units can be interconverted easily, if needed, by the previous equations.