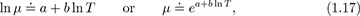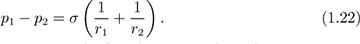Fluid Mechanics for Chemical Engineers

This chapter is from the book

Fluid Mechanics for Chemical Engineers: with Microfluidics, CFD, and COMSOL Multiphysics 5, 3rd Edition

Learn More Buy

This chapter is from the book

This chapter is from the book 

Fluid Mechanics for Chemical Engineers: with Microfluidics, CFD, and COMSOL Multiphysics 5, 3rd Edition

Learn More Buy

1.4 Physical Properties—Density, Viscosity, and Surface Tension

There are three physical properties of fluids that are particularly important: density, viscosity, and surface tension. Each of these will be defined and viewed briefly in terms of molecular concepts, and their dimensions will be examined in terms of mass, length, and time (M, L, and T). The physical properties depend primarily on the particular fluid. For liquids, viscosity also depends strongly on the temperature; for gases, viscosity is approximately proportional to the square root of the absolute temperature. The density of gases depends almost directly on the absolute pressure; for most other cases, the effect of pressure on physical properties can be disregarded.

Typical processes often run almost isothermally, and in these cases the effect of temperature can be ignored. Except in certain special cases, such as the flow of a compressible gas (in which the density is not constant) or a liquid under a very high shear rate (in which viscous dissipation can cause significant internal heating), or situations involving exothermic or endothermic reactions, we shall ignore any variation of physical properties with pressure and temperature.

Density. Density depends on the mass of an individual molecule and the number of such molecules that occupy a unit of volume. For liquids, density depends primarily on the particular liquid and, to a much smaller extent, on its temperature. Representative densities of liquids are given in Table 1.1.² (See Eqns. (1.9)–(1.11) for an explanation of the specific gravity and coefficient of thermal expansion columns.) The accuracy of the values given in Tables 1.1–1.6 is adequate for the calculations needed in this text. However, if highly accurate values are needed, particularly at extreme conditions, then specialized information should be sought elsewhere.

Table 1.1 Specific Gravities, Densities, and Thermal Expansion Coefficients of Liquids at 20° C

The density ρ of a fluid is defined as its mass per unit volume and indicates its inertia or resistance to an accelerating force. Thus:

in which the notation “[=]” is consistently used to indicate the dimensions of a quantity.³ It is usually understood in Eqn. (1.5) that the volume is chosen so that it is neither so small that it has no chance of containing a representative selection of molecules nor so large that (in the case of gases) changes of pressure cause significant changes of density throughout the volume. A medium characterized by a density is called a continuum and follows the classical laws of mechanics—including Newton’s law of motion, as described in this book.

Degrees API (American Petroleum Institute) are related to specific gravity s by the formula:

Note that for water, ° API = 10, with correspondingly higher values for liquids that are less dense. Thus, for the crude oil listed in Table 1.1, Eqn. (1.6) indeed gives 141.5/0.851 – 131.5 ≐ 35 ° API.

Densities of gases. For ideal gases, pV = nRT, where p is the absolute pressure, V is the volume of the gas, n is the number of moles (abbreviated as “mol” when used as a unit), R is the gas constant, and T is the absolute temperature. If M_w is the molecular weight of the gas, it follows that:

Thus, the density of an ideal gas depends on the molecular weight, absolute pressure, and absolute temperature. Values of the gas constant R are given in Table 1.2 for various systems of units. Note that degrees Kelvin, formerly represented by “ °K,” is now more simply denoted as “K.”

Table 1.2 Values of the Gas Constant, R

For a nonideal gas, the compressibility factor Z (a function of p and T) is introduced into the denominator of Eqn. (1.7), giving:

Thus, the extent to which Z deviates from unity gives a measure of the nonideality of the gas.

The isothermal compressibility of a gas is defined as:

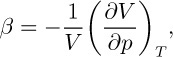
and equals—at constant temperature—the fractional decrease in volume caused by a unit increase in the pressure. For an ideal gas, β = 1/p, the reciprocal of the absolute pressure.

The coefficient of thermal expansion α of a material is its isobaric (constant pressure) fractional increase in volume per unit rise in temperature:

Since, for a given mass, density is inversely proportional to volume, it follows that for moderate temperature ranges (over which α is essentially constant) the density of most liquids is approximately a linear function of temperature:

where ρ₀ is the density at a reference temperature T₀. For an ideal gas, α = 1/T, the reciprocal of the absolute temperature.

The specific gravity s of a fluid is the ratio of the density ρ to the density ρ_SC of a reference fluid at some standard condition:

For liquids, ρ_SC is usually the density of water at 4 °C, which equals 1.000 g/ml or 1,000 kg/m³. For gases, ρ_SC is sometimes taken as the density of air at 60 °F and 14.7 psia, which is approximately 0.0759 lb_m/ft³, and sometimes at 0 °C and one atmosphere absolute; since there is no single standard for gases, care must obviously be taken when interpreting published values. For natural gas, consisting primarily of methane and other hydrocarbons, the gas gravity is defined as the ratio of the molecular weight of the gas to that of air (28.8 lb_m/lb-mol).

Values of the molecular weight M_w are listed in Table 1.3 for several commonly occurring gases, together with their densities at standard conditions of atmospheric pressure and 0 °C.

Table 1.3 Gas Molecular Weights and Densities (the Latter at Atmospheric Pressure and 0 °C)

Viscosity. The viscosity of a fluid measures its resistance to flow under an applied shear stress, as shown in Fig. 1.8(a). There, the fluid is ideally supposed to be confined in a relatively small gap of thickness h between one plate that is stationary and another plate that is moving steadily at a velocity V relative to the first plate.

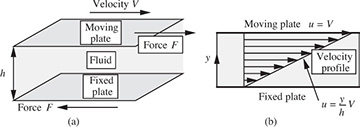
Fig. 1.8 (a) Fluid in shear between parallel plates; (b) the ensuing linear velocity profile.

In practice, the situation would essentially be realized by a fluid occupying the space between two concentric cylinders of large radii rotating relative to each other, as in Fig. 1.1. A steady force F to the right is applied to the upper plate (and, to preserve equilibrium, to the left on the lower plate) in order to maintain a constant motion and to overcome the viscous friction caused by layers of molecules sliding over one another.

Under these circumstances, the velocity u of the fluid to the right is found experimentally to vary linearly from zero at the lower plate (y = 0) to V itself at the upper plate, as in Fig. 1.8(b), corresponding to no-slip conditions at each plate. At any intermediate distance y from the lower plate, the velocity is simply:

Recall that the shear stress τ is the tangential applied force F per unit area:

in which A is the area of each plate. Experimentally, for a large class of materials, called Newtonian fluids, the shear stress is directly proportional to the velocity gradient:

The proportionality constant μ is called the viscosity of the fluid; its dimensions can be found by substituting those for F (ML/T²), A (L²), and du/dy (T⁻¹), giving:

Representative units for viscosity are g/cm s (also known as poise, designated by P), kg/m s, and lb_m/ft hr. The centipoise (cP), one hundredth of a poise, is also a convenient unit, since the viscosity of water at room temperature is approximately 0.01 P or 1.0 cP. Table 1.11 gives viscosity conversion factors.

The viscosity of a fluid may be determined by observing the pressure drop when it flows at a known rate in a tube, as analyzed in Section 3.2. More sophisticated methods for determining the rheological or flow properties of fluids—including viscosity—are also discussed in Chapter 11; such methods often involve containing the fluid in a small gap between two surfaces, moving one of the surfaces, and measuring the force needed to maintain the other surface stationary.

The kinematic viscosity ν is the ratio of the viscosity to the density:

and is important in cases in which significant viscous and gravitational forces coexist. The reader can check that the dimensions of ν are L²/T, which are identical to those for the diffusion coefficient 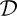in mass transfer and for the thermal diffusivity α = k/ρc_p in heat transfer. There is a definite analogy among the three quantities—indeed, as seen later, the value of the kinematic viscosity governs the rate of “diffusion” of momentum in the laminar and turbulent flow of fluids.

Viscosities of liquids. The viscosities μ of liquids generally vary approximately with absolute temperature T according to:

and—to a good approximation—are independent of pressure. Assuming that μ is measured in centipoise and that T is either in degrees Kelvin or Rankine, appropriate parameters a and b are given in Table 1.4 for several representative liquids. The resulting values for viscosity are approximate, suitable for a first design only.

Table 1.4 Viscosity Parameters for Liquids

Viscosities of gases. The viscosity μ of many gases is approximated by the formula:

in which T is the absolute temperature (Kelvin or Rankine), μ₀ is the viscosity at an absolute reference temperature T₀, and n is an empirical exponent that best fits the experimental data. The values of the parameters μ₀ and n for atmospheric pressure are given in Table 1.5; recall that to a first approximation, the viscosity of a gas is independent of pressure. The values μ₀ are given in centipoise and correspond to a reference temperature of T₀ ≐ 273 K ≐ 492 °R.

Table 1.5 Viscosity Parameters for Gases

Surface tension.⁴ Surface tension is the tendency of the surface of a liquid to behave like a stretched elastic membrane. There is a natural tendency for liquids to minimize their surface area. The obvious case is that of a liquid droplet on a horizontal surface that is not wetted by the liquid—mercury on glass, or water on a surface that also has a thin oil film on it. For small droplets, such as those on the left of Fig. 1.9, the droplet adopts a shape that is almost perfectly spherical, because in this configuration there is the least surface area for a given volume.

Fig. 1.9 The larger droplets are flatter because gravity is becoming more important than surface tension.

For larger droplets, the shape becomes somewhat flatter because of the increasingly important gravitational effect, which is roughly proportional to a³, where a is the approximate droplet radius, whereas the surface area is proportional only to a². Thus, the ratio of gravitational to surface tension effects depends roughly on the value of a³/a² = a, and is therefore increasingly important for the larger droplets, as shown to the right in Fig. 1.9. Overall, the situation is very similar to that of a water-filled balloon, in which the water accounts for the gravitational effect and the balloon acts like the surface tension.

A fundamental property is the surface energy, which is defined with reference to Fig. 1.10(a). A molecule I, situated in the interior of the liquid, is attracted equally in all directions by its neighbors. However, a molecule S, situated in the surface, experiences a net attractive force into the bulk of the liquid. (The vapor above the surface, being comparatively rarefied, exerts a negligible force on molecule S.) Therefore, work has to be done against such a force in bringing an interior molecule to the surface. Hence, an energy σ, called the surface energy, can be attributed to a unit area of the surface.

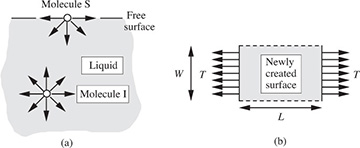
Fig. 1.10 (a) Molecules in the interior and surface of a liquid; (b) newly created surface caused by moving the tension T through a distance L.

An equivalent viewpoint is to consider the surface tension T existing per unit distance of a line drawn in the surface, as shown in Fig. 1.10(b). Suppose that such a tension has moved a distance L, thereby creating an area WL of fresh surface. The work done is the product of the force, TW, and the distance L through which it moves, namely TWL, and this must equal the newly acquired surface energy σWL. Therefore, T = σ; both quantities have units of force per unit distance, such as N/m, which is equivalent to energy per unit area, such as J/m².

We next find the amount p₁−p₂, by which the pressure p₁ inside a liquid droplet of radius r, shown in Fig. 1.11(a), exceeds the pressure p₂ of the surrounding vapor. Fig. 1.11(b) illustrates the equilibrium of the upper hemisphere of the droplet, which is also surrounded by an imaginary cylindrical “control surface” ABCD, on which forces in the vertical direction will soon be equated. Observe that the internal pressure p₁ is trying to blow apart the two hemispheres (the lower one is not shown), whereas the surface tension σ is trying to pull them together.

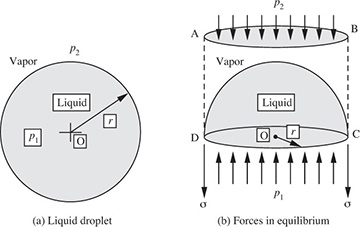
Fig. 1.11 Pressure change across a curved surface.

In more detail, there are two different types of forces to be considered:

1. That due to the pressure difference between the pressure inside the droplet and the vapor outside, each acting on an area πr² (that of the circles CD and AB):

   

2. That due to surface tension, which acts on the circumference of length 2πr:

   

At equilibrium, these two forces are equated, giving:

That is, there is a higher pressure on the concave or droplet side of the interface. What would the pressure change be for a bubble instead of a droplet? Why?

More generally, if an interface has principal radii of curvature r₁ and r₂, the increase in pressure can be shown to be:

For a sphere of radius r, as in Fig. 1.11, both radii are equal, so that r₁ = r₂ = r, and p₁ – p₂ = 2σ/r. Problem 1.31 involves a situation in which r₁ ≠ r₂. The radii r₁ and r₂ will have the same sign if the corresponding centers of curvature are on the same side of the interface; if not, they will be of opposite sign. Appendix A contains further information about the curvature of a surface.

A brief description of simple experiments for measuring the surface tension σ of a liquid, shown in Fig. 1.12, now follows:

Fig. 1.12 Methods for measuring surface tension.

(a) In the capillary-rise method, a narrow tube of internal radius a is dipped vertically into a pool of liquid, which then rises to a height h inside the tube; if the contact angle (the angle between the free surface and the wall) is θ, the meniscus will be approximated by part of the surface of a sphere; from the geometry shown in the enlargement on the right-hand side of Fig. 1.12(a), the radius of the sphere is seen to be r = a/ cos θ. Since the surface is now concave on the air side, the reverse of Eqn. (1.21) occurs, and p₂ = p₁ – 2σ/r, so that p₂ is below atmospheric pressure p₁. Now follow the path 1–2–3–4, and observe that p₄ = p₃ because points 3 and 4 are at the same elevation in the same liquid. Thus, the pressure at point 4 is:

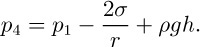
However, p₄ = p₁ since both of these are at atmospheric pressure. Hence, the surface tension is given by the relation:

In many cases—for complete wetting of the surface—θ is essentially zero and cos θ = 1. However, for liquids such as mercury in glass, there may be a complete non-wetting of the surface, in which case θ = π, so that cos θ = –1; the result is that the liquid level in the capillary is then depressed below that in the surrounding pool.

(b) In the drop-weight method, a liquid droplet is allowed to form very slowly at the tip of a capillary tube of outer diameter D. The droplet will eventually grow to a size where its weight just overcomes the surface-tension force πDσ holding it up. At this stage, it will detach from the tube, and its weight w = Mg can be determined by catching it in a small pan and weighing it. By equating the two forces, the surface tension is then calculated from:

(c) In the ring tensiometer, a thin wire ring, suspended from the arm of a sensitive balance, is dipped into the liquid and gently raised, so that it brings a thin liquid film up with it. The force F needed to support the film is measured by the balance. The downward force exerted on a unit length of the ring by one side of the film is the surface tension; since there are two sides to the film, the total force is 2Pσ, where P is the circumference of the ring. The surface tension is therefore determined as:

In common with most experimental techniques, all three methods described above require slight modifications to the results expressed in Eqns. (1.23)–(1.25) because of imperfections in the simple theories.

Surface tension generally appears only in situations involving either free surfaces (liquid/gas or liquid/solid boundaries) or interfaces (liquid/liquid boundaries); in the latter case, it is usually called the interfacial tension.

Representative values for the surface tensions of liquids at 20° C, in contact either with air or their vapor (there is usually little difference between the two), are given in Table 1.6.⁵

Table 1.6 Surface Tensions