- Dummy Coding
- Effect Coding
- Orthogonal Coding
- Factorial Analysis
- Statistical Power, Type I and Type II Errors
- Coping with Unequal Cell Sizes
Coping with Unequal Cell Sizes
In Chapter 6 we looked at the combined effects of unequal group sizes and unequal variances on the nominal probability of a given t-ratio with a given degrees of freedom. You saw that the results can differ from the expected probabilities depending on whether the larger or the smaller group has the larger variance. You saw how Welch’s correction can help compensate for unequal cell sizes.
Things are more complicated with more than just two groups (as in a t-test), particularly in factorial designs with two or more factors. Then, there are several—rather than just two—groups to compare as to both group size and variance.
In a design with at least two factors, and therefore at least four cells, several options exist, based primarily on the models comparison approach that is discussed at some length in Chapter 5. Unfortunately, these approaches do not have names that are generally accepted. Of the two discussed in this section, one is sometimes termed the regression approach and sometimes the experimental design approach; the other is sometimes termed the sequential approach and sometimes the a priori ordering approach. There are other terms in use. I use experimental design and sequential here.
The additional difficulty imposed by factorial designs when cell sizes are unequal concerns correlations between the vectors that define group membership: the 1’s, 0’s and −1’s used in dummy, effect and orthogonal coding. Recall from earlier chapters that with equal cell sizes, the correlations between the vectors are largely 0.0. That feature means the sums of squares (and equivalently the variance) of the outcome variable can be assigned unambiguously to one vector or another.
But when the vectors are correlated, the unambiguous assignment of variability to a given vector becomes ambiguous. The vectors share variance with the outcome variable, of course. If they didn’t there would be little point to retaining them in the analysis. But with unequal cell frequencies, the vectors share variance not only with the outcome variable but with one another, and in that case it’s not possible to tell whether, say, 2% of the outcome variance belongs to Factor A, to Factor B, or to some sort of shared assignment such as 1.5% and 0.5%.
Despite the fact that I’ve cast this problem in terms of the vectors used in multiple regression analysis, the traditional ANOVA approaches are subject to the problem too.
But there’s no single, generally applicable answer to the problem in the traditional framework either. The reliance there is typically on proportional (if unequal) cell frequencies and unweighted means analysis. Most current statistical packages use one of the approaches discussed here, or on one of their near relatives. (Not that it’s representative of applications such as SAS or R, but Excel’s Data Analysis add-in does not support designs with unequal cell frequencies in its 2-Factor ANOVA tool.)
Using the Regression Approach
This approach is also termed the unique approach because it treats each vector as though it were the last to enter the regression equation. If, say, a factor named Treatment is the last to enter the equation, all the other sources of regression variation are already in the equation and any variance shared by Treatment with the other vectors has already been assigned to them. Therefore, any remaining variance attributable to Treatment belongs to Treatment alone. It’s unique to the Treatment vector.
Figure 7.25 shows an example of how this works.
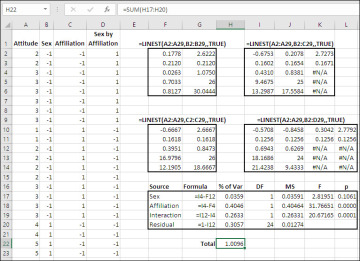
Figure 7.25 This design has four cells with different numbers of observations.
The idea is to use the models comparison approach to isolate the variance explained uniquely by each variable. Generally, we want to assess the factors one by one, before moving on to their interactions. So the process with this design is to subtract the variance explained by each main effect from the variance explained by all the main effects.
For example, in Figure 7.25, the range F10:G14 returns LINEST() results for Attitude, the outcome variable, regressed onto Affiliation, one of the two factors. Affiliation explains 39.51% of the variability in Attitude when Affiliation is the only vector entered: see cell F12.
Similarly, the range I2:K6 returns LINEST() results for the regression of Attitude on Sex and Affiliation. Cell I4 shows that together, Sex and Affiliation account for 43.1% of the variance in Attitude.
Therefore, with this data set, we can conclude that 43.10% − 39.51%, or 3.59%, of the variability in the outcome measure is specifically and uniquely attributable to the Sex factor: the proportion attributable to the two main effects less that attributable to Affiliation. This finding, 3.59%, differs from the result obtained from the LINEST() analysis in F2:G6, where cell F4 tells us that Sex accounts for 2.63% of the variance in the outcome measure. The difference between 3.59% and 2.63% is due to the fact that the unequal cell frequencies induce correlations between the vectors, introducing ambiguity into how the variance is allocated to the vectors.
The proportion of variance due to Affiliation is calculated in the same fashion. The proportion returned by LINEST() for the outcome measure regressed onto Sex, in cell F4, is subtracted from (once again) the proportion for both main effects, in cell I4. The result of that subtraction is 40.46%, a bit more than the 39.51% returned by the single factor LINEST() in cell F12.
After the two main effects, Sex and Affiliation, are assessed individually by subtracting their proportions of variance from the proportion accounted for by both, the analysis moves on to the interaction of the main effects. That’s managed by subtracting the proportion of variance for the main effects, returned by LINEST() in cell I4, from the total proportion explained by the main effects and the interaction, returned by LINEST() in cell I12.
We can test the statistical significance of each main effect and the interaction in an ANOVA table, substituting proportions of total variance for sums of squares. That’s done in the range F17:L20. Just divide the proportion of variance associated with each source of variation by its degrees of freedom to get a stand in for the mean square. Divide the mean square for each main effect and for the interaction by the mean square residual to obtain the F-ratio for each factor and for the interaction. The F-ratios are tested as usual with Excel’s F.DIST.RT() function.
This analysis can be duplicated for sums of squares instead of proportions of variance, simply by multiplying each proportion by the sum of the squared deviations of the outcome variable from the grand mean.
Notice, by the way, in cell H22 that the proportions of variance do not total to precisely 100.00%, although the total is quite close. With unequal cell frequencies, even when managed by this unique variance approach, the total of the proportions of variance is not necessarily equal to exactly 100%. If you were working with sums of squares rather than proportions of variance, the factors’ sums of squares do not necessarily add up precisely to the total sum of squares. Again, this is due to the adjustment of each factor and interaction vector for its correlation with the other vectors.
The sequential approach to dealing with unequal cell frequencies and correlated vectors, discussed in the next section, usually leads to a somewhat different outcome.
Sequential Variance Assignment
Bear in mind that the technique discussed in this section is just one of several methods for dealing with unequal cell frequencies in factorial designs. The unique assignment technique, described in the preceding section, is another such method. It differs from the sequential method in that it adjusts each factor’s contribution to the regression sum of squares for that of the other factor or factors. In the sequential method, factors that are entered earlier are not adjusted for factors entered later.
Figure 7.26 shows how the sequential method works.
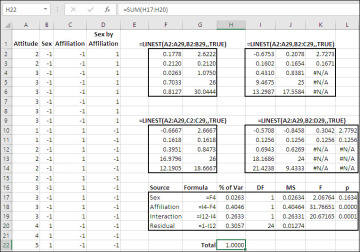
Figure 7.26 Consider using the sequential approach when one factor might have a causal effect on another.
Figure 7.26 includes only two changes from Figure 7.25, but they can turn out to be important. In the sequential analysis shown in Figure 7.26, the variability associated with the Sex variable is unadjusted for its correlation with the Affiliation variable, whereas that adjustment occurs in Figure 7.25. Compare cell H17 in the two figures.
Here’s the rationale for the difference. In this data set, the subjects are categorized according to their sex and their party affiliation. It is known that, nationally, women show a moderate preference for registering as Democrats rather than as Republicans, and the reverse is true for men. Therefore, any random sample of registered voters will have unequal cell frequencies (unless the researcher takes steps to ensure equal group sizes, a dubious practice at best when the variables are not directly under experimental control). And with those unequal cell frequencies come the correlations between the coded vectors that we’re trying to deal with.
In this and similar cases, however, there’s a good argument for assigning all the variance shared by Sex and Affiliation to the Sex variable. The reasoning is that a person’s sex might influence his or her political preference (mediated, no doubt, by social and cultural variables that are sensitive to a person’s sex). The reverse idea, that a person’s sex is influenced by his or her choice of political party, is absurd.
Therefore, it’s arguable that variance shared by Sex and Affiliation is due to Sex and not to Affiliation. In turn, that argues for allowing the Sex variable to retain all the variance that it can claim in a single factor analysis, and not to adjust the variance attributed to Sex according to its correlation with Affiliation.
In that case you can use the entire proportion of variance attributable to Sex in a single factor analysis as its proportion in the full analysis. That’s what has been done in Figure 7.26, where the formula in cell H17 is:
=F4
instead of this:
=I4-F12
in cell H17 of Figure 7.25. In that figure, the variance attributable to the Sex factor is adjusted by subtracting the variance attributable to the Affiliation factor (cell F12) from the variance attributable to both main effects (cell I4). But in Figure 7.26, the variance attributable to Sex in a single-factor analysis in cell F4 is used in cell H17, unadjusted for variance it shares with Affiliation. Again, this is because in the researcher’s judgment any variance shared by the two factors belongs to the Sex variable as, to some degree, causing variability in the Affiliation factor.
The adjustment, or the lack thereof, makes no practical difference in this case: The variance attributable to Sex is so small that it will not approach statistical significance whether it is adjusted or not. But with a different data set, the decision to adjust one variable for another as in the unique variance approach, or to retain the first factor’s full variance, as in the sequential approach, could easily make a meaningful difference.
Notice, by the way, in Figure 7.26 that the coded vectors have in effect been made orthogonal to one another. The total of the proportions of variance in the range H17:H20 now comes to 1.000, as shown in cell H22. That demonstrates that the overlap in variability has been removed by the decision not to adjust Sex’s variance for its correlation with Affiliation.
Why not follow the sequential approach in all cases? Because you need a good, sound reason to treat one factor as causal with respect to other factors. In this case, the fact of causality is underscored by the patterns in the full population, and the logic of the situation argues for the directionality of the cause: that Sex causes Affiliation rather than the other way around.
Nevertheless, this is a case in which the subjects assign themselves to groups by being of one sex or the other and by deciding which political party to belong to. If the researcher were to selectively discard subjects in order to achieve equal group sizes, without regard to causality, he would be artificially imposing orthogonality on the variables. So doing alters the reality of the situation, and you therefore need to be able to show that causality exists and what its direction is.
This consideration does not tend to arise in true experimental designs, where the researcher is in a position to randomly assign subjects to treatments and conditions. Broccoli plants are not in a position to decide whether they prefer organic or inorganic fertilizer, or whether they flourish in sun or in shade.
Let’s move on to Chapter 8 now, and look further into the effect of adding a covariate to your design.

