The Art of Computer Programming: Random Numbers

This chapter is from the book

Art of Computer Programming, Volume 2: Seminumerical Algorithms, 3rd Edition

Learn More Buy

This chapter is from the book

This chapter is from the book 

Art of Computer Programming, Volume 2: Seminumerical Algorithms, 3rd Edition

Learn More Buy

Click to view larger image

• Any one who considers arithmetical methods of producing random digits is, of course, in a state of sin.

  — JOHN VON NEUMANN (1951)

• Lest men suspect your tale untrue, Keep probability in view.

  — JOHN GAY (1727)

• There wanted not some beams of light to guide men in the exercise of their Stocastick faculty.

  — JOHN OWEN (1662)

3.1. Introduction

Numbers that are “chosen at random” are useful in many different kinds of applications. For example:

1. Simulation. When a computer is being used to simulate natural phenomena, random numbers are required to make things realistic. Simulation covers many fields, from the study of nuclear physics (where particles are subject to random collisions) to operations research (where people come into, say, an airport at random intervals).
2. Sampling. It is often impractical to examine all possible cases, but a random sample will provide insight into what constitutes “typical” behavior.
3. Numerical analysis. Ingenious techniques for solving complicated numerical problems have been devised using random numbers. Several books have been written on this subject.
4. Computer programming. Random values make a good source of data for testing the effectiveness of computer algorithms. More importantly, they are crucial to the operation of randomized algorithms, which are often far superior to their deterministic counterparts. This use of random numbers is the primary application of interest to us in this series of books; it accounts for the fact that random numbers are already being considered here in Chapter 3, before most of the other computer algorithms have appeared.
5. Decision making. There are reports that many executives make their decisions by flipping a coin or by throwing darts, etc. It is also rumored that some college professors prepare their grades on such a basis. Sometimes it is important to make a completely “unbiased” decision. Randomness is also an essential part of optimal strategies in the theory of matrix games.
6. Cryptography. A source of unbiased bits is crucial for many types of secure communications, when data needs to be concealed.

7. Aesthetics. A little bit of randomness makes computer-generated graphics and music seem more lively. For example, a pattern like

   

   Click to view larger image

   in certain contexts. [See D. E. Knuth, Bull. Amer. Math. Soc. 1 (1979), 369.]

8. Recreation. Rolling dice, shuffling decks of cards, spinning roulette wheels, etc., are fascinating pastimes for just about everybody. These traditional uses of random numbers have suggested the name “Monte Carlo method,” a general term used to describe any algorithm that employs random numbers.

People who think about this topic almost invariably get into philosophical discussions about what the word “random” means. In a sense, there is no such thing as a random number; for example, is 2 a random number? Rather, we speak of a sequence of independent random numbers with a specified distribution, and this means loosely that each number was obtained merely by chance, having nothing to do with other numbers of the sequence, and that each number has a specified probability of falling in any given range of values.

A uniform distribution on a finite set of numbers is one in which each possible number is equally probable. A distribution is generally understood to be uniform unless some other distribution is specifically mentioned.

Each of the ten digits 0 through 9 will occur about 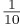of the time in a (uniform) sequence of random digits. Each pair of two successive digits should occur about 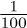of the time, and so on. Yet if we take a truly random sequence of a million digits, it will not always have exactly 100,000 zeros, 100,000 ones, etc. In fact, chances of this are quite slim; a sequence of such sequences will have this character on the average.

Any specified sequence of a million digits is as probable as any other. Thus, if we are choosing a million digits at random and if the first 999,999 of them happen to come out to be zero, the chance that the final digit is zero is still exactly 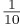, in a truly random situation. These statements seem paradoxical to many people, yet no contradiction is really involved.

There are several ways to formulate decent abstract definitions of randomness, and we will return to this interesting subject in Section 3.5; but for the moment, let us content ourselves with an intuitive understanding of the concept.

Many years ago, people who needed random numbers in their scientific work would draw balls out of a “well-stirred urn,” or they would roll dice or deal out cards. A table of over 40,000 random digits, “taken at random from census reports,” was published in 1927 by L. H. C. Tippett. Since then, a number of devices have been built to generate random numbers mechanically. The first such machine was used in 1939 by M. G. Kendall and B. Babington-Smith to produce a table of 100,000 random digits. The Ferranti Mark I computer, first installed in 1951, had a built-in instruction that put 20 random bits into the accumulator using a resistance noise generator; this feature had been recommended by A. M. Turing. In 1955, the RAND Corporation published a widely used table of a million random digits obtained with the help of another special device. A famous random-number machine called ERNIE has been used for many years to pick the winning numbers in the British Premium Savings Bonds lottery. [F. N. David describes the early history in Games, Gods, and Gambling (1962). See also Kendall and Babington-Smith, J. Royal Stat. Soc. A101 (1938), 147–166; B6 (1939), 51–61; S. H. Lavington’s discussion of the Mark I in CACM 21 (1978), 4–12; the review of the RAND table in Math. Comp. 10 (1956), 39–43; and the discussion of ERNIE by W. E. Thomson, J. Royal Stat. Soc. A122 (1959), 301–333.]

Shortly after computers were introduced, people began to search for efficient ways to obtain random numbers within computer programs. A table could be used, but this method is of limited utility because of the memory space and input time requirement, because the table may be too short, and because it is a bit of a nuisance to prepare and maintain the table. A machine such as ERNIE might be attached to the computer, as in the Ferranti Mark I, but this has proved to be unsatisfactory since it is impossible to reproduce calculations exactly a second time when checking out a program; moreover, such machines have tended to suffer from malfunctions that are extremely difficult to detect. Advances in technology made tables useful again during the 1990s, because a billion well-tested random bytes could easily be made accessible. George Marsaglia helped resuscitate random tables in 1995 by preparing a demonstration disk that contained 650 random megabytes, generated by combining the output of a noise-diode circuit with deterministically scrambled rap music. (He called it “white and black noise.”)

The inadequacy of mechanical methods in the early days led to an interest in the production of random numbers using a computer’s ordinary arithmetic operations. John von Neumann first suggested this approach in about 1946; his idea was to take the square of the previous random number and to extract the middle digits. For example, if we are generating 10-digit numbers and the previous value was 5772156649, we square it to get

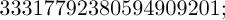
the next number is therefore 7923805949.

There is a fairly obvious objection to this technique: How can a sequence generated in such a way be random, since each number is completely determined by its predecessor? (See von Neumann’s comment at the beginning of this chapter.) The answer is that the sequence isn’t random, but it appears to be. In typical applications the actual relationship between one number and its successor has no physical significance; hence the nonrandom character is not really undesirable. Intuitively, the middle square seems to be a fairly good scrambling of the previous number.

Sequences generated in a deterministic way such as this are often called pseudorandom or quasirandom sequences in the highbrow technical literature, but in most places of this book we shall simply call them random sequences, with the understanding that they only appear to be random. Being “apparently random” is perhaps all that can be said about any random sequence anyway. Random numbers generated deterministically on computers have worked quite well in nearly every application, provided that a suitable method has been carefully selected. Of course, deterministic sequences aren’t always the answer; they certainly shouldn’t replace ERNIE for the lotteries.

Von Neumann’s original “middle-square method” has actually proved to be a comparatively poor source of random numbers. The danger is that the sequence tends to get into a rut, a short cycle of repeating elements. For example, if zero ever appears as a number of the sequence, it will continually perpetuate itself.

Several people experimented with the middle-square method in the early 1950s. Working with numbers that have four digits instead of ten, G. E. Forsythe tried 16 different starting values and found that 12 of them led to sequences ending with the cycle 6100, 2100, 4100, 8100, 6100, . . . , while two of them degenerated to zero. More extensive tests were carried out by N. Metropolis, mostly in the binary number system. He showed that when 20-bit numbers are being used, there are 13 different cycles into which the middle-square sequence might degenerate, the longest of which has a period of length 142.

It is fairly easy to restart the middle-square method on a new value when zero has been detected, but long cycles are somewhat harder to avoid. Exercises 6 and 7 discuss some interesting ways to determine the cycles of periodic sequences, using very little memory space.

A theoretical disadvantage of the middle-square method is given in exercises 9 and 10. On the other hand, working with 38-bit numbers, Metropolis obtained a sequence of about 750,000 numbers before degeneracy occurred, and the resulting 750,000 × 38 bits satisfactorily passed statistical tests for randomness. [Symp. on Monte Carlo Methods (Wiley, 1956), 29–36.] This experience showed that the middle-square method can give usable results, but it is rather dangerous to put much faith in it until after elaborate computations have been performed.

Many random number generators in use when this chapter was first written were not very good. People have traditionally tended to avoid learning about such subroutines; old methods that were comparatively unsatisfactory have been passed down blindly from one programmer to another, until the users have no understanding of the original limitations. We shall see in this chapter that the most important facts about random number generators are not difficult to learn, although prudence is necessary to avoid common pitfalls.

It is not easy to invent a foolproof source of random numbers. This fact was convincingly impressed upon the author in 1959, when he attempted to create a fantastically good generator using the following peculiar approach:

Algorithm K (“Super-random” number generator). Given a 10-digit decimal number X, this algorithm may be used to change X to the number that should come next in a supposedly random sequence. Although the algorithm might be expected to yield quite a random sequence, reasons given below show that it is not, in fact, very good at all. (The reader need not study this algorithm in great detail except to observe how complicated it is; note, in particular, steps K1 and K2.)

• K1. [Choose number of iterations.] Set Y ← ⌊X/10⁹⌋, the most significant digit of X. (We will execute steps K2 through K13 exactly Y + 1 times; that is, we will apply randomizing transformations a random number of times.)
• K2. [Choose random step.] Set Z ← ⌊X/10⁸⌋ mod 10, the second most significant digit of X. Go to step K(3 + Z). (That is, we now jump to a random step in the program.)
• K3. [Ensure ≥ 5 × 10⁹.] If X < 5000000000, set X ← X + 5000000000.
• K4. [Middle square.] Replace X by ⌊X²/10⁵⌋ mod 10¹⁰, that is, by the middle of the square of X.
• K5. [Multiply.] Replace X by (1001001001 X) mod 10¹⁰.
• K6. [Pseudo-complement.] If X < 100000000, then set X ← X + 9814055677; otherwise set X ← 10¹⁰ – X.
• K7. [Interchange halves.] Interchange the low-order five digits of X with the high-order five digits; that is, set X ← 10⁵(X mod 10⁵) + ⌊X/10⁵⌋, the middle 10 digits of (10¹⁰ + 1)X.
• K8. [Multiply.] Same as step K5.
• K9. [Decrease digits.] Decrease each nonzero digit of the decimal representation of X by one.
• K10. [99999 modify.] If X < 10⁵, set X ← X² + 99999; otherwise set X ← X – 99999.
• K11. [Normalize.] (At this point X cannot be zero.) If X < 10⁹, set X ← 10X and repeat this step.
• K12. [Modified middle square.] Replace X by ⌊X(X − 1)/10⁵⌋ mod 10¹⁰, that is, by the middle 10 digits of X(X − 1).
• K13. [Repeat?] If Y > 0, decrease Y by 1 and return to step K2. If Y = 0, the algorithm terminates with X as the desired “random” value.

(The machine-language program corresponding to this algorithm was intended to be so complicated that a person reading a listing of it without explanatory comments wouldn’t know what the program was doing.)

Considering all the contortions of Algorithm K, doesn’t it seem plausible that it should produce almost an infinite supply of unbelievably random numbers? No! In fact, when this algorithm was first put onto a computer, it almost immediately converged to the 10-digit value 6065038420, which—by extraordinary coincidence—is transformed into itself by the algorithm (see Table 1). With another starting number, the sequence began to repeat after 7401 values, in a cyclic period of length 3178.

Table 1 A Colossal Coincidence: The Number 6065038420 is Transformed Into Itself by Algorithm K.

The moral of this story is that random numbers should not be generated with a method chosen at random. Some theory should be used.

In the following sections we shall consider random number generators that are superior to the middle-square method and to Algorithm K. The corresponding sequences are guaranteed to have certain desirable random properties, and no degeneracy will occur. We shall explore the reasons for this random-like behavior in some detail, and we shall also consider techniques for manipulating random numbers. For example, one of our investigations will be the shuffling of a simulated deck of cards within a computer program.

Section 3.6 summarizes this chapter and lists several bibliographic sources.

Exercises

1. [20] Suppose that you wish to obtain a decimal digit at random, not using a computer. Which of the following methods would be suitable?

1. Open a telephone directory to a random place by sticking your finger in it somewhere, and use the units digit of the first number found on the selected page.
2. Same as (a), but use the units digit of the page number.
3. Roll a die that is in the shape of a regular icosahedron, whose twenty faces have been labeled with the digits 0, 0, 1, 1, . . . , 9, 9. Use the digit that appears on top, when the die comes to rest. (A felt-covered table with a hard surface is recommended for rolling dice.)
4. Expose a geiger counter to a source of radioactivity for one minute (shielding yourself) and use the units digit of the resulting count. Assume that the geiger counter displays the number of counts in decimal notation, and that the count is initially zero.
5. Glance at your wristwatch; and if the position of the second-hand is between 6n and 6(n + 1) seconds, choose the digit n.
6. Ask a friend to think of a random digit, and use the digit he names.
7. Ask an enemy to think of a random digit, and use the digit he names.
8. Assume that 10 horses are entered in a race and that you know nothing whatever about their qualifications. Assign to these horses the digits 0 to 9, in arbitrary fashion, and after the race use the winner’s digit.

2. [M22] In a random sequence of a million decimal digits, what is the probability that there are exactly 100,000 of each possible digit?

3. [10] What number follows 1010101010 in the middle-square method?

4. [20] (a) Why can’t the value of X be zero when step K11 of Algorithm K is performed? What would be wrong with the algorithm if X could be zero? (b) Use Table 1 to deduce what happens when Algorithm K is applied repeatedly with the starting value X = 3830951656.

5. [15] Explain why, in any case, Algorithm K should not be expected to provide infinitely many random numbers, in the sense that (even if the coincidence given in Table 1 had not occurred) one knows in advance that any sequence generated by Algorithm K will eventually be periodic.

6. [M21] Suppose that we want to generate a sequence of integers X₀, X₁, X₂, . . . , in the range 0 ≤ X_n < m. Let f(x) be any function such that 0 ≤ x < m implies 0 ≤ f(x) < m. Consider a sequence formed by the rule X_n+1 = f(X_n). (Examples are the middle-square method and Algorithm K.)

1. Show that the sequence is ultimately periodic, in the sense that there exist numbers λ and μ for which the values

   

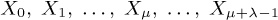
   are distinct, but X_n+λ = X_n when n ≥ μ. Find the maximum and minimum possible values of μ and λ.

2. (R. W. Floyd.) Show that there exists an n > 0 such that X_n = X_2n; and the smallest such value of n lies in the range μ ≤ n ≤ μ + λ. Furthermore the value of X_n is unique in the sense that if X_n = X_2n and X_r = X_2r, then X_r = X_n.
3. Use the idea of part (b) to design an algorithm that calculates μ and λ for any given function f and any given X₀, using only O(μ + λ) steps and only a bounded number of memory locations.

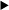7. [M21] (R. P. Brent, 1977.) Let ℓ(n) be the greatest power of 2 that is less than or equal to n; thus, for example, ℓ(15) = 8 and ℓ(ℓ(n)) = ℓ(n).

1. Show that, in terms of the notation in exercise 6, there exists an n > 0 such that X_n = X_ℓ(n)–1. Find a formula that expresses the least such n in terms of the periodicity numbers μ and λ.
2. Apply this result to design an algorithm that can be used in conjunction with any random number generator of the type X_n+1 = f(X_n), to prevent it from cycling indefinitely. Your algorithm should calculate the period length λ, and it should use only a small amount of memory space—you must not simply store all of the computed sequence values!

8. [23] Make a complete examination of the middle-square method in the case of two-digit decimal numbers.

1. We might start the process out with any of the 100 possible values 00, 01, . . . , 99. How many of these values lead ultimately to the repeating cycle 00, 00, . . . ? [Example: Starting with 43, we obtain the sequence 43, 84, 05, 02, 00, 00, 00, . . . .]
2. How many possible final cycles are there? How long is the longest cycle?
3. What starting value or values will give the largest number of distinct elements before the sequence repeats?

9. [M14] Prove that the middle-square method using 2n-digit numbers to the base b has the following disadvantage: If the sequence includes any number whose most significant n digits are zero, the succeeding numbers will get smaller and smaller until zero occurs repeatedly.

10. [M16] Under the assumptions of the preceding exercise, what can you say about the sequence of numbers following X if the least significant n digits of X are zero? What if the least significant n + 1 digits are zero?

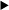11. [M26] Consider sequences of random number generators having the form described in exercise 6. If we choose f(x) and X₀ at random—in other words, if we assume that each of the m^m possible functions f(x) is equally probable and that each of the m possible values of X₀ is equally probable—what is the probability that the sequence will eventually degenerate into a cycle of length λ = 1? [Note: The assumptions of this problem give a natural way to think of a “random” random number generator of this type. A method such as Algorithm K may be expected to behave somewhat like the generator considered here; the answer to this problem gives a measure of how colossal the coincidence of Table 1 really is.]

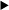12. [M31] Under the assumptions of the preceding exercise, what is the average length of the final cycle? What is the average length of the sequence before it begins to cycle? (In the notation of exercise 6, we wish to examine the average values of λ and of μ + λ.)

13. [M42] If f(x) is chosen at random in the sense of exercise 11, what is the average length of the longest cycle obtainable by varying the starting value X₀? [Note: We have already considered the analogous problem in the case that f(x) is a random permutation; see exercise 1.3.3–23.]

14. [M38] If f(x) is chosen at random in the sense of exercise 11, what is the average number of distinct final cycles obtainable by varying the starting value? [See exercise 8(b).]

15. [M15] If f(x) is chosen at random in the sense of exercise 11, what is the probability that none of the final cycles has length 1, regardless of the choice of X₀?

16. [15] A sequence generated as in exercise 6 must begin to repeat after at most m values have been generated. Suppose we generalize the method so that X_n+1 depends on X_n−1 as well as on X_n; formally, let f(x, y) be a function such that 0 ≤ x, y < m implies 0 ≤ f(x, y) < m. The sequence is constructed by selecting X₀ and X₁ arbitrarily, and then letting

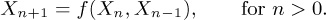
What is the maximum period conceivably attainable in this case?

17. [10] Generalize the situation in the previous exercise so that X_n+1 depends on the preceding k values of the sequence.

18. [M20] Invent a method analogous to that of exercise 7 for finding cycles in the general form of random number generator discussed in exercise 17.

19. [HM47] Solve the problems of exercises 11 through 15 asymptotically for the more general case that X_n+1 depends on the preceding k values of the sequence; each of the m^mk functions f(x₁, . . . , x_k) is to be considered equally probable. [Note: The number of functions that yield the maximum period is analyzed in exercise 2.3.4.2–23.]

20. [30] Find all nonnegative X < 10¹⁰ that lead ultimately via Algorithm K to the self-reproducing number in Table 1.

21. [40] Prove or disprove: The mapping X ↦ f(X) defined by Algorithm K has exactly five cycles, of lengths 3178, 1606, 1024, 943, and 1.

22. [21] (H. Rolletschek.) Would it be a good idea to generate random numbers by using the sequence f(0), f(1), f(2), . . . , where f is a random function, instead of using x₀, f(x₀), f(f(x₀)), etc.?

23. [M26] (D. Foata and A. Fuchs, 1970.) Show that each of the m^m functions f(x) considered in exercise 6 can be represented as a sequence (x₀, x₁, . . . , x_m−1) having the following properties:

1. (x₀, x₁, . . . , x_m−1) is a permutation of (f(0), f(1), . . . , f(m − 1)).
2. (f(0), . . . , f(m − 1)) can be uniquely reconstructed from (x₀, x₁, . . . , x_m−1).
3. The elements that appear in cycles of f are {x₀, x₁, . . . , x_k−1}, where k is the largest subscript such that these k elements are distinct.
4. x_j ∉ {x₀, x₁, . . . , x_j−1} implies x_j−1 = f(x_j), unless x_j is the smallest element in a cycle of f.
5. (f(0), f(1), . . . , f(m − 1)) is a permutation of (0, 1, . . . , m − 1) if and only if (x₀, x₁, . . . , x_m−1) represents the inverse of that permutation by the “unusual correspondence” of Section 1.3.3.
6. x₀ = x₁ if and only if (x₁, . . . , x_m−1) represents an oriented tree by the construction of exercise 2.3.4.4–18, with f(x) the parent of x.