3.10. Constraint Blocks
Like a block, a constraint block is an element of definition—one that defines a Boolean constraint expression (an expression that must evaluate to either true or false). Most often, the constraint expression you define in a constraint block is an equation or an inequality: a mathematical relationship that you use to constrain value properties of blocks. You would do this for two reasons:
- To specify assertions about valid system values in an operational system
- To perform engineering analyses during the design stage of the life cycle
The variables in a constraint expression are called constraint parameters. Generally, they represent quantities, and so they’re typed most often by value types. For example, Figure 3.26 shows a constraint block named Transfer Orbit Size, which defines a constraint expression that contains three constraint parameters: semimajorAxis, initialOrbit-Radius, and finalOrbitRadius. These three constraint parameters are typed by the value type km.
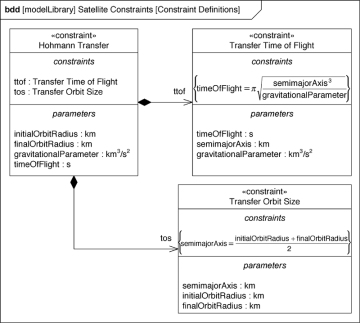
Figure 3.26 Relationships between constraint blocks
Constraint parameters receive their values from the value properties they’re bound to—that is, the value properties that are being constrained. At any given moment, those values either satisfy the constraint expression, or they don’t; the system is either operating nominally, or it isn’t. Note, however, that a BDD by itself can’t convey which constraint parameters and value properties are bound to one another. You would express this piece of information on a parametric diagram. (I discuss this in detail in Chapter 9.)
The notation for a constraint block on a BDD is a rectangle with the stereotype «constraint» preceding the name. The constraint expression always appears between curly brackets ({}) in the constraints compartment. The constraint parameters in the constraint expression are listed individually in the parameters compartment.
You sometimes build a more complex constraint block from a set of simpler constraint blocks. You would do this to create a more complex mathematical relationship from simpler equations and inequalities. The more complex constraint block can display its constituent parts as a list of constraint properties in the constraints compartment. Recall from Section 3.4.1.4 that a constraint property has a name and a type in the format name : type. The type, as mentioned earlier, must be the name of a constraint block.
For example, Figure 3.26 shows that the constraint block Hohmann Transfer is composed of two constraint properties—ttof and tos—which represent usages of the constraint blocks Transfer Time of Flight and Transfer Orbit Size, respectively. This model conveys that Hohmann Transfer defines a constraint expression that is a composite of two simpler constraint expressions—in effect, defining a more complex mathematical relationship.
Note, though, what this BDD doesn’t (and can’t) convey: where those two simpler constraint expressions are specifically connected to each other to create the composite constraint expression. A parametric diagram would convey this additional piece of information (more on this in Chapter 9).
As an alternative to the constraints compartment notation, you can use composite associations to convey that one constraint block is composed of other, simpler ones (as shown in Figure 3.26). Note that the role names shown on the part ends of the two composite associations correspond to the names of the constraint properties in the Hohmann Transfer constraint block. These are equivalent notations. You use composite associations when you need to expose the details of the simpler constraint blocks; in contrast, you use the constraints compartment notation to hide those details when they’re not the focus of the diagram.
