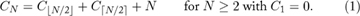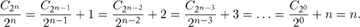This chapter is from the book
This chapter is from the book
This chapter is from the book
1.2. Theory of Algorithms
The prime goal of the theory of algorithms is to classify algorithms according to their performance characteristics. The following mathematical notations are convenient for doing so:
Definition Given a function f(N),
O(f(N)) denotes the set of all g(N) such that |g(N)/f(N)| is bounded from above as N → ∞.
Ω(f(N)) denotes the set of all g(N) such that |g(N)/f(N)| is bounded from below by a (strictly) positive number as N → ∞.
Θ(f(N)) denotes the set of all g(N) such that |g(N)/f(N)| is bounded from both above and below as N → ∞.
These notations, adapted from classical analysis, were advocated for use in the analysis of algorithms in a paper by Knuth in 1976 [21]. They have come into widespread use for making mathematical statements about bounds on the performance of algorithms. The O-notation provides a way to express an upper bound; the Ω-notation provides a way to express a lower bound; and the Θ-notation provides a way to express matching upper and lower bounds.
In mathematics, the most common use of the O-notation is in the context of asymptotic series. We will consider this usage in detail in Chapter 4. In the theory of algorithms, the O-notation is typically used for three purposes: to hide constants that might be irrelevant or inconvenient to compute, to express a relatively small “error” term in an expression describing the running time of an algorithm, and to bound the worst case. Nowadays, the Ω-and Θ- notations are directly associated with the theory of algorithms, though similar notations are used in mathematics (see [21]).
Since constant factors are being ignored, derivation of mathematical results using these notations is simpler than if more precise answers are sought. For example, both the “natural” logarithm lnN ≡ logeN and the “binary” logarithm lgN ≡ log2N often arise, but they are related by a constant factor, so we can refer to either as being O(logN) if we are not interested in more precision. More to the point, we might say that the running time of an algorithm is Θ(NlogN) seconds just based on an analysis of the frequency of execution of fundamental operations and an assumption that each operation takes a constant number of seconds on a given computer, without working out the precise value of the constant.
Exercise 1.1 Show that f(N) = NlgN + O(N) implies that f(N) = Θ(NlogN).
As an illustration of the use of these notations to study the performance characteristics of algorithms, we consider methods for sorting a set of numbers in an array. The input is the numbers in the array, in arbitrary and unknown order; the output is the same numbers in the array, rearranged in ascending order. This is a well-studied and fundamental problem: we will consider an algorithm for solving it, then show that algorithm to be “optimal” in a precise technical sense.
First, we will show that it is possible to solve the sorting problem efficiently, using a well-known recursive algorithm called mergesort. Mergesort and nearly all of the algorithms treated in this book are described in detail in Sedgewick and Wayne [30], so we give only a brief description here. Readers interested in further details on variants of the algorithms, implementations, and applications are also encouraged to consult the books by Cormen, Leiserson, Rivest, and Stein [6], Gonnet and Baeza-Yates [11], Knuth [17][18][19][20], Sedgewick [26], and other sources.
Mergesort divides the array in the middle, sorts the two halves (recursively), and then merges the resulting sorted halves together to produce the sorted result, as shown in the Java implementation in Program 1.1. Mergesort is prototypical of the well-known divide-and-conquer algorithm design paradigm, where a problem is solved by (recursively) solving smaller subproblems and using the solutions to solve the original problem. We will analyze a number of such algorithms in this book. The recursive structure of algorithms like mergesort leads immediately to mathematical descriptions of their performance characteristics.
To accomplish the merge, Program 1.1 uses two auxiliary arrays b and c to hold the subarrays (for the sake of efficiency, it is best to declare these arrays external to the recursive method). Invoking this method with the call mergesort(0, N-1) will sort the array a[0...N-1]. After the recursive calls, the two halves of the array are sorted. Then we move the first half of a[] to an auxiliary array b[] and the second half of a[] to another auxiliary array c[]. We add a “sentinel” INFTY that is assumed to be larger than all the elements to the end of each of the auxiliary arrays, to help accomplish the task of moving the remainder of one of the auxiliary arrays back to a after the other one has been exhausted. With these preparations, the merge is easily accomplished: for each k, move the smaller of the elements b[i] and c[j] to a[k], then increment k and i or j accordingly.
Program 1.1. Mergesort
private void mergesort(int[] a, int lo, int hi)
{
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
mergesort(a, lo, mid);
mergesort(a, mid + 1, hi);
for (int k = lo; k <= mid; k++)
b[k-lo] = a[k];
for (int k = mid+1; k <= hi; k++)
c[k-mid-1] = a[k];
b[mid-lo+1] = INFTY; c[hi - mid] = INFTY;
int i = 0, j = 0;
for (int k = lo; k <= hi; k++)
if (c[j] < b[i]) a[k] = c[j++];
else a[k] = b[i++];
}
Exercise 1.2 In some situations, defining a sentinel value may be inconvenient or impractical. Implement a mergesort that avoids doing so (see Sedgewick [26] for various strategies).
Exercise 1.3 Implement a mergesort that divides the array into three equal parts, sorts them, and does a three-way merge. Empirically compare its running time with standard mergesort.
In the present context, mergesort is significant because it is guaranteed to be as efficient as any sorting method can be. To make this claim more precise, we begin by analyzing the dominant factor in the running time of mergesort, the number of compares that it uses.
Theorem 1.1. (Mergesort compares).
Mergesort uses NlgN + O(N) compares to sort an array of N elements.
Proof. If CN is the number of compares that the Program 1.1 uses to sort N elements, then the number of compares to sort the first half is C⌊N/2⌋, the number of compares to sort the second half is C⌈N/2⌉, and the number of compares for the merge is N (one for each value of the index k). In other words, the number of compares for mergesort is precisely described by the recurrence relation
)
To get an indication for the nature of the solution to this recurrence, we consider the case when N is a power of 2:
- C2n = 2C2n–1 + 2n for n ≥ 1 with C1 = 0.
Dividing both sides of this equation by 2n, we find that
)
This proves that CN = NlgN when N = 2n; the theorem for general N follows from (1) by induction. The exact solution turns out to be rather complicated, depending on properties of the binary representation of N. In Chapter 2 we will examine how to solve such recurrences in detail.
Exercise 1.4 Develop a recurrence describing the quantity CN+1 – CN and use this to prove that
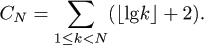
Exercise 1.5 Prove that CN = N⌈lgN⌉ + N – 2⌈lgN⌉.
Exercise 1.6 Analyze the number of compares used by the three-way mergesort proposed in Exercise 1.2.
For most computers, the relative costs of the elementary operations used Program 1.1 will be related by a constant factor, as they are all integer multiples of the cost of a basic instruction cycle. Furthermore, the total running time of the program will be within a constant factor of the number of compares. Therefore, a reasonable hypothesis is that the running time of merge-sort will be within a constant factor of NlgN.
From a theoretical standpoint, mergesort demonstrates that NlogN is an “upper bound” on the intrinsic difficulty of the sorting problem:
- There exists an algorithm that can sort any N-element file in time proportional to NlogN.
A full proof of this requires a careful model of the computer to be used in terms of the operations involved and the time they take, but the result holds under rather generous assumptions. We say that the “time complexity of sorting is O(NlogN).”
Exercise 1.7 Assume that the running time of mergesort is cNlgN + dN, where c and d are machine-dependent constants. Show that if we implement the program on a particular machine and observe a running time tN for some value of N, then we can accurately estimate the running time for 2N by 2tN (1 + 1/lgN), independent of the machine.
Exercise 1.8 Implement mergesort on one or more computers, observe the running time for N = 1,000,000, and predict the running time for N = 10,000,000 as in the previous exercise. Then observe the running time for N = 10,000,000 and calculate the percentage accuracy of the prediction.
The running time of mergesort as implemented here depends only on the number of elements in the array being sorted, not on the way they are arranged. For many other sorting methods, the running time may vary substantially as a function of the initial ordering of the input. Typically, in the theory of algorithms, we are most interested in worst-case performance, since it can provide a guarantee on the performance characteristics of the algorithm no matter what the input is; in the analysis of particular algorithms, we are most interested in average-case performance for a reasonable input model, since that can provide a path to predict performance on “typical” input.
We always seek better algorithms, and a natural question that arises is whether there might be a sorting algorithm with asymptotically better performance than mergesort. The following classical result from the theory of algorithms says, in essence, that there is not.
From a theoretical standpoint, this result demonstrates that NlogN is a “lower bound” on the intrinsic difficulty of the sorting problem:
- All compare-based sorting algorithms require time proportional to NlogN to sort some N-element input file.
This is a general statement about an entire class of algorithms. We say that the “time complexity of sorting is Ω(NlogN).” This lower bound is significant because it matches the upper bound of Theorem 1.1, thus showing that mergesort is optimal in the sense that no algorithm can have a better asymptotic running time. We say that the “time complexity of sorting is Θ(NlogN).” From a theoretical standpoint, this completes the “solution” of the sorting “problem:” matching upper and lower bounds have been proved.
Again, these results hold under rather generous assumptions, though they are perhaps not as general as it might seem. For example, the results say nothing about sorting algorithms that do not use compares. Indeed, there exist sorting methods based on index calculation techniques (such as those discussed in Chapter 9) that run in linear time on average.
Exercise 1.9 Suppose that it is known that each of the items in an N-item array has one of two distinct values. Give a sorting method that takes time proportional to N.
Exercise 1.10 Answer the previous exercise for three distinct values.
We have omitted many details that relate to proper modeling of computers and programs in the proofs of Theorem 1.1 and Theorem 1.2. The essence of the theory of algorithms is the development of complete models within which the intrinsic difficulty of important problems can be assessed and “efficient” algorithms representing upper bounds matching these lower bounds can be developed. For many important problem domains there is still a significant gap between the lower and upper bounds on asymptotic worst-case performance. The theory of algorithms provides guidance in the development of new algorithms for such problems. We want algorithms that can lower known upper bounds, but there is no point in searching for an algorithm that performs better than known lower bounds (except perhaps by looking for one that violates conditions of the model upon which a lower bound is based!).
Thus, the theory of algorithms provides a way to classify algorithms according to their asymptotic performance. However, the very process of approximate analysis (“within a constant factor”) that extends the applicability of theoretical results often limits our ability to accurately predict the performance characteristics of any particular algorithm. More important, the theory of algorithms is usually based on worst-case analysis, which can be overly pessimistic and not as helpful in predicting actual performance as an average-case analysis. This is not relevant for algorithms like mergesort (where the running time is not so dependent on the input), but average-case analysis can help us discover that nonoptimal algorithms are sometimes faster in practice, as we will see. The theory of algorithms can help us to identify good algorithms, but then it is of interest to refine the analysis to be able to more intelligently compare and improve them. To do so, we need precise knowledge about the performance characteristics of the particular computer being used and mathematical techniques for accurately determining the frequency of execution of fundamental operations. In this book, we concentrate on such techniques.