- 1.1 Introduction
- 1.2 The Molecular Nature of Energy, Temperature, and Pressure
- 1.3 The Molecular Nature of Entropy
- 1.4 Basic Concepts
- 1.5 Real Fluids and Tabulated Properties
- 1.6 Summary
- 1.7 Practice Problems
- 1.8 Homework Problems
1.2 The Molecular Nature of Energy, Temperature, and Pressure
Energy is a term that applies to many aspects of a system. Its formal definition is in terms of the capability to perform work. We will not quantify the potential for work until the next chapter, but you should have some concept of work from your course in introductory physics. Energy may take the form of kinetic energy or potential energy, and it may refer to energy of a macroscopic or a molecular scale.
- Energy is the sum total of all capacity for doing work that is associated with matter: kinetic, potential, submolecular (i.e., molecular rearrangements by reaction), or subatomic (e.g., ionization, fission).
- Kinetic energy is the energy associated with motion of a system. Motion can be classified as translational, rotational, or vibrational.
- Temperature is related to the "hotness" of a substance, but is fundamentally related to the kinetic energy of the constituitive atoms.
- Potential energy is the energy associated with a system due to its position in a force field.
In the study of "energy movements," we will continually ask, "How much energy is here now, and how much is there?" In the process, we need to establish a point for beginning our calculations. According to the definition above, we might intuitively represent zero internal energy by a perfect vacuum. But then, knowing the internal energy of a single proton inside the vacuum would require knowing how much energy it takes to make a proton from nothing. Since this is not entirely practical, this intuitive choice is not a good engineering choice usually. This is essentially the line of reasoning that gives rise to the convention of calculating energy changes relative to a reference state. Thus, there is no absolute reference point that is always the most convenient; there are only changes in energy from one state to another. We select reference conditions that are relevant throughout any particular process of interest. Depending on the complexity of the calculation, reference conditions may vary from, say, defining the enthalpy (to be defined later) of liquid water to be zero at 0.01°C (as in the steam tables) to setting it equal to zero for the molecular hydrogen and oxygen at 1 bar and 298.15 K (as in the heat of reaction), depending on the situation. Since this text focuses on changes in kinetic energy, potential energy, and energies of reaction, we need not specify reference states any more fundamental than the elements, and thus we do not consider subatomic particles.
Kinetic Energy and Temperature
Kinetic energy is commonly introduced in detail during introductory physics as 1/2 mv2, where m is the mass of the object and v is the object velocity. Atomic species that make up solids are frozen in localized positions, but they are continuously vibrating with kinetic energy. Fluids such as liquids and gases are not frozen into fixed positions and move through space with kinetic energy and collide with one another.
The most reliable definition of temperature is that it is a numerical scale for uniquely ordering the "hotness" of a series of objects.3 However, this "hotness" is coupled to the molecular kinetic energy of the constituent molecules in a fundamental way. The relation between kinetic energy and temperature is surprisingly direct. When we touch a hot object, the kinetic energy of the object is transferred to our hand via the atoms vibrating at the surface. Temperature is proportional to the average molecular kinetic energy. The expression is easiest to use in engineering on a molar basis. For a monatomic substance
Equation 1.1
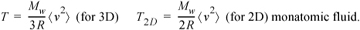
where <> brackets denote an average, and Mw is the molecular weight. We use a subscript for the temperature of 2D motion to avoid confusion with the more common 3D motion. The differences between 2D and 3D temperature are explained on page 22. For a polyatomic molecule, the temperature is coupled to the average velocity of the individual atoms, but some of the motion of the bonded atoms results in vibrations and rotations rather than a direct translation of the center of mass and thus it is not directly related to the velocity of the center of mass. (See Section 7.10 on page 276.)
Eqn. 1.1 is applicable to any classical monatomic system, including liquids and solids. This means that for a pure system of a monatomic ideal gas in thermal equilibrium with a liquid, the average velocities of the molecules are independent of the phase in which they reside. We can infer this behavior by envisioning gas atoms exchanging energy with the solid container walls and then the solid exchanging energy with the liquid. At equilibrium, all exchanges of energy must reach the same kinetic energy distribution. The liquid molecular environment is different from the gas molecular environment because liquid molecules are confined to move primarily within a much more crowded environment where the potential energies are more significant. When a molecule's kinetic energy is insufficient to escape the potential energy (we discuss the potential energy next) due to molecular attractiveness, the atoms simply collide with a higher frequency in their local environment. What happens if the temperature is raised such that the liquid molecules can escape the potential energies of the neighbors? We call this phenomenon "boiling." Now you can begin to understand what temperature is and how it relates to other important thermodynamic properties.
We are guaranteed that a universal scale of temperature can be developed because of the zeroth law of thermodynamics: If two objects are in equilibrium with a third, then they are in equilibrium with one another as we discussed in the previous paragraph. The zeroth law is a law in the sense that it is a fact of experience that must be regarded as an empirical fact of nature. The significance of the zeroth law is that we can calibrate the temperature of any new object by equilibrating it with objects of known temperature. Temperature is therefore an empirical scale that requires calibration according to specific standards. The Celsius and Fahrenheit scales are in everyday use. The conversions are:
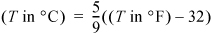
When we perform thermodynamic calculations, we must usually use absolute temperature in Kelvin or Rankine. These scales are related by
- (T in K) = (T in °C) + 273.15
- (T in °R) = (T in °F) + 459.67
- (T in R) = 1.8 · (T in K)
The absolute temperature scale has the advantage that the temperature can never be less than absolute zero. This observation is easily understood from the kinetic perspective. The kinetic energy cannot be less than zero; if the atoms are moving, their kinetic energy must be greater than zero.
Potential Energy
Solids and liquids exist due to the intermolecular potential energy (molecular "stickiness') of atoms. If molecules were not "sticky" all matter would be gases or solids. Thus, the principles of molecular potential energy are important for developing a molecular perspective on the nature of liquids, solids, and non-ideal gases. Potential energy is associated with the "work" of moving a system some distance through a force field. On the macroscopic scale, we are well aware of the effect of gravity. As an example, the Earth and the moon are two spherical bodies which are attracted by a force which varies as r–2. The potential energy represents the work of moving the two bodies closer together or farther apart, which is simply the integral of the force over distance. (The force is the negative derivative of potential with respect to distance.) Thus, the potential function varies as r–1. Potential energies are similar at the microscopic level except that the forces vary with position according to different laws. The gravitational attraction between two individual atoms is insignificant because the masses are so small. Rather, the important forces are due to the nature of the atomic orbitals. For a rigorous description, the origin of the intermolecular potential is traced back to the solution of SchrÖdinger's quantum mechanics for the motions of electrons around nuclei. However, we do not need to perform quantum mechanics to understand the principles.
Intermolecular Potential Energy
Atoms are composed of dense nuclei of positive charge with electron densities of negative charge built around the nucleus in shells. The outermost shell is referred to as the valence shell. Electron density often tends to concentrate in lobes in the valence orbitals for common elements like C, N, O, F, S, and Cl. These lobes may be occupied by bonded atoms that are coordinated in specific geometries, such as the tetrahedron in CH4, or they may be occupied by unbonded electron pairs that fill out the valence as in NH3 or H2O, or they may be widely "shared" as in a resonance or aromatic structure. These elements (H, C, N, O, F, S, Cl) and some noble gases like He, Ne, and Ar provide virtually all of the building blocks for the molecules to be considered in this text.
By considering the implications of atomic structure and atomic collisions, it is possible to develop the following subclassifications of intermolecular forces:
- Electrostatic forces between charged particles (ions) and between permanent dipoles, quadrupoles, and higher multipoles.
- Induction forces between a permanent dipole (or quadrupole) and an induced dipole.
- Forces of attraction (dispersion forces) due to the polarizability of electron clouds and repulsion due to prohibited overlap.
- Specific (chemical) forces leading to association and complex formation, especially evident in the case of hydrogen bonding.
Attractive forces are quantified by negative numerical values, and repulsive forces will be characterized by positive numerical values. To a first approximation, these forces can be characterized by a spherically averaged model of the intermolecular potential (aka. "potential" model). The potential, u ( r), is the work (integral of force over distance) of bringing two molecules from infinite distance to a specific distance, r . When atoms are far apart (as in a low-pressure gas), they do not sense one another and interaction energy approaches zero. When the atoms are within about two diameters, they attract, resulting in a negative energy of interaction. Because they have finite size, as they are brought closer, they resist overlap. Thus, at very close distances, the forces are repulsive and create very large positive potential energies. These intuitive features are illustrated graphically in Fig. 1.1. The discussion below provides a brief background on why these forces exist and how they vary with distance.
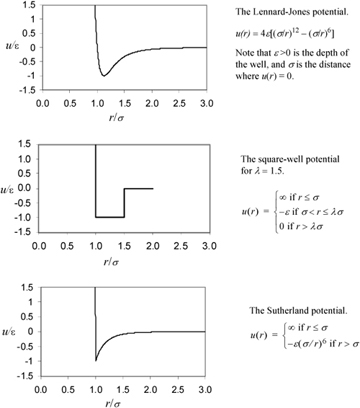
Figure 1.1 Schematics of three engineering models for pair potentials on a dimensionless basis.
Electrostatic Forces
The force between two point charges described by Coulomb's Law is very similar to the law of gravitation and should be familiar from elementary courses in chemistry and physics,
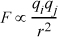
where qi and qj are the charges, and r is the separation of centers. Upon integration, u = 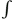 Fdr, the potential energy is proportional to inverse distance,
Fdr, the potential energy is proportional to inverse distance,
Equation 1.2
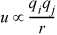
If all molecules were perfectly spherical and rigid, the only way that these electrostatic interactions could come into play is through the presence of ions. But a molecule like NH3 is not perfectly spherical. NH3 has three protons on one side and a lobe of electron density in the unbonded valence shell electron pair. This permanent asymmetric distribution of charge density is modeled mathematically with a dipole (+ and – charge separation) on the NH3 molecule.4 This means that ammonia molecules lined up with the electrons facing one another repel while molecules lined up with the electrons facing the protons will attract. Since electrostatic energy drops off asr–1, one might expect that the impact of these forces would be long-range. Fortunately, with the close proximity of the positive charge to the negative charge in a molecule like NH3, the charges tend to cancel one another as the molecule spins and tumbles about through a fluid. This spinning and tumbling makes it reasonable to consider a spherical average of the intermolecular energy as a function of distance that may be constructed by averaging over all orientations between the molecules at each distance. In a large collection of molecules randomly distributed relative to one another, this averaging approach gives rise to many cancellations, and the net impact is approximately
Equation 1.3

where k = R/NA is Boltzmann's constant, related to the gas constant, R, and Avogadro's number,NA. This surprisingly simple result is responsible for a large part of the attractive energy between polar molecules. This energy is attractive because the molecules tend to spend somewhat more time lined up attractively than repulsively, and the r–6 power arises from the averaging that occurs as the molecules tumble and the attractive forces decrease with separation. A key feature of dipole-dipole forces is the temperature dependence.
Induction Forces
When a molecule with a permanent dipole approaches a molecule with no dipole, the positive charge of the dipolar molecule will tend to pull electron density away from the nonpolar molecule and "induce" a dipole moment into the nonpolar molecule. The magnitude of this effect depends on the strength of the dipole and how tightly the orbitals of the nonpolar molecule constrain the electrons spatially in an electric field, characterized by the "polarizability."5 For example, the pi bonding in benzene makes it fairly polarizable. A similar consideration of the spherical averaging described in relation to electrostatic forces results again in a dependence of r–6 as approximately
Equation 1.4
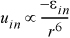
Disperse Attraction Forces (Dispersion Forces)
When two nonpolar molecules approach, they may also induce dipoles into one another owing to fluctuating distributions of electrons. Their dependence on radial distance may be analyzed and gives the form for the attractive forces:
Equation 1.5
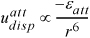
Note that dipole-dipole, induction, and dispersion forces all vary as r –6.
Repulsive Forces
The forces become repulsive rapidly as radial distance decreases, and quickly outweighs the attractive force as the atoms are forced into the same space. A common empirical equation is
Equation 1.6
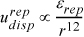
Engineering Potential Models
Based on the forms of these electrostatic, induction, and dispersion forces, it should be easy to appreciate the form of the Lennard-Jones potential in Fig. 1.1. Other approximate models of the potential function are possible, such as the square-well potential or the Sutherland potential also shown in Fig. 1.1. These simplified potential models are accurate enough for many applications.
The key features of all of these potential models are the representation of the size of the molecule by the parameter σ and the attractive strength (i.e. "stickiness") by the parameter ε. We can gain considerable insight about the thermodynamics of fluids by intuitively reasoning about the relatively simple effects of size and stickiness. For example, if we represent molecules by lumping together all the atomic sites, a large molecule like buckminsterfullerene (solid at room temperature) would have a larger value for σ and ε than would methane (gas at room temperature). Water and methane are about the same size, but their difference in boiling temperature indicates a large difference in their stickiness. Considering the molecular perspective, it should become apparent that water has a higher boiling temperature because it sticks to itself more strongly than does methane. With these simple insights, you should be able to understand the molecular basis for many macroscopic phenomena. Example 1.1 illustrates several computations for intermolecular potential energy.
When we sum the potential energy for a collection of molecules, we often call the sum configurational energy to differentiate quantity from the potential energy which is commonly used when discussing atoms or sites.
Note that we would need a more complicated potential model to represent the shape of the molecule. Typically, molecules of different shapes are represented by binding together several potentials like those above with each potential site representing one molecular segment. For example, n-butane could be represented by four Lennard-Jones sites that have their relative centers located at distances corresponding to the bond-lengths in n-butane. The potential between two butane molecules would then be the sum of the potentials between each of the individual Lennard-Jones sites on the different molecules. In similar fashion, potential models for very complex molecules can be constructed.
Potentials in Mixtures
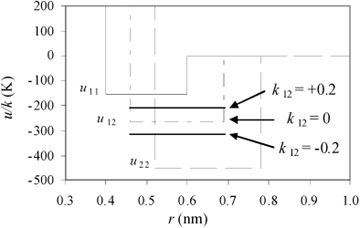
Our discussion of intermolecular potentials has focused on describing single molecules, but it is actually more interesting to contemplate the potential models for different molecules that are mixed together. Note that the square-well model provides a simple way for use to consider only the potential energy of the closest neighbors. We can use the square-well potential as the basis for this analysis and focus simply on the size (σij) and stickiness (εij) of each potential model, where the subscript ij indicates an interaction of molecule i with molecule j. Commonly, we assume that λ = 1.5 in discussions of the square-well potential, unless otherwise specified. For example, ε11 would be the stickiness of molecule 1 to itself, and ε12 would be its stickiness to a molecule of type 2 and ε21=ε12. We often calculate the interactions of dissimilar molecules by using combining rules that relate the interaction to the parameters of the sites. Commonly we use combining rules developed by Lorentz and Bertholet. The size parameter for interaction between different molecules is reasonably well represented by
Equation 1.7
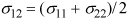
This rule simply states that the distance between two touching molecules is equal to the radius of the first one plus the radius of the second one. The estimation of the stickiness parameter for interaction between different molecules requires more empirical reasoning. It is conventional to estimate the stickiness by a geometric mean, but to permit flexibility to adjust the approximate rule by adding an adjustable constant that can be refined using experimental measurements, or sometimes using theories like quantum mechanical simulation. For historical reasons, this constant is typically referred to as "kij" or the binary interaction parameter, and defined through the following rule:
Equation 1.8
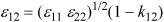
The default value is k12 = 0.
Specific (Chemical) Forces Like Hydrogen Bonding
What happens when the strength of interaction between two molecules is so strong at certain orientations that it does not make sense to spherically average over it? Hydrogen bonding is an example of such an interaction, as you probably know from an introductory chemistry or biology course. For instance, it would not make sense to spherically average when two atoms preferentially interact in a specific orientation. But, if they were covalently bonded, we would call that a chemical reaction and handle it in a different way. An interesting problem arises when the strength of interaction is too strong to be treated entirely by spherically averaging and too weak to be treated as a normal chemical reaction which forms permanent stable chemical species. Clearly, this problem is difficult and it would be tempting to try to ignore it. In fact, most of this course will deal with theories that treat only what can be derived by spherically averaging. But it should be kept in mind that these specific forces are responsible for some rather important properties, especially in the form of hydrogen bonding. Since many systems are aqueous or contain amides or alcohols, ignoring hydrogen bonding entirely would substantially undermine the accuracy of our conceptual foundation. Furthermore, the concept of favorable energetic interactions between acids and bases can lend broad insights into the mysteries of chemical formulations. As an engineering approach, we can make large adjustments to the spherical nature of these forces such that we can often approximate them with a single characteristic constant to obtain a workable engineering model. Example 1.2 illustrates the concept of combining rules that pervades the entirety of mixture thermodynamics.
Internal Energy
We have taken considerable time to develop the molecular aspects of kinetic and potential energy. These molecular properties are of great importance, but for large-scale macroscopic process system calculations, these microscopic energies are combined and we consider kinetic and configurational energy collectively as the internal energy of the system, which is given the symbol U. It may be somewhat confusing that kinetic and potential energy exist on the macroscopic level and the microscopic level. The potential energy (gravitational potential energy) and kinetic energy of the center of mass of the system are accounted for separately. The internal energy is a function of the temperature and density (the latter for non-ideal gases) of the system, and it does not usually change if the entire system is placed on, say, an airplane where the kinetic and potential energy of the center of mass differ considerably from a stationary position on the ground. This is the convention followed throughout the remainder of Unit I. In Units II and III, we reexamine the molecular potentials as to how they affect the bulk fluid properties. Thus, throughout the remainder of Unit I, when we refer to kinetic and potential energy of a body of fluid as a system, we are referring to the kinetic energy of the center of mass of the system and the gravitational potential energy of the center of mass of the system.
 Energy will be tabulated relative to a convenient reference state.
Energy will be tabulated relative to a convenient reference state.