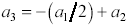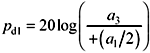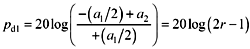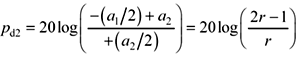- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.14 Linear Equalization: Long Backplane Trace Example
Figure 3.43 depicts the propagation function for four 50-Ω striplines with different lengths. The longest trace (1.5 m) corresponds to the maximal configuration you might encounter in a large backplane if you include long daughter card traces at each end.
)
Figure 3.43. The propagation function for a long pcb trace varies strongly with trace length.
The propagation functions in this collection exhibit low-pass filter traits that are characteristic of a combination of skin and dielectric loss effects: The longer the trace, the lower the 3dB attenuation frequency.
Figure 3.44 illustrates the signal as received at the far end of each trace. The signal pattern used to generate this figure is 1111101111100000100000, transmitted at a bit rate of 2.5 Gb/s (400-ps bit intervals). The assumed transmit rise/fall time is 20% of a bit interval. This particular pattern (a maximal run length of ones interrupted by a single zero, and vice versa) is a good worst-case eye-opening test for many systems whose transfer function declines monotonically like the curves shown in Figure 3.43.
)
Figure 3.44. The received signal amplitude varies as a function of line length.
The shortest trace (0.1 m) conveys the signal with almost perfect fidelity. As the trace is lengthened, the quick transition (101) is attenuated by successively greater amounts until, at 1.5 meters, this transition fails to adequately cross the receiver threshold. The attenuation is caused by dispersion of the rising and falling edges of the signal—in a quick 101 pattern the signal does not have adequate time to completely cross the threshold before it must reverse course.
Note that a sine wave purely composed of the alternating 101010.... pattern would of course cross the threshold admirably in both directions. A long run of ones, however, followed by one quick pop in the downward direction (or the inverse of this pattern), presents the greatest difficulty.
Figure 3.45 details the exact amplitudes of the received signal at several points. The peak-to-peak amplitude of a large (slow-speed, or long run-length) transition is marked as a1. The peak-to-peak amplitude of a quick 010 transition is marked as a2. The magnitude by which the peak of the 010 sequence manages to top the receiver threshold is given as
)
)
Figure 3.45. The dispersion penalty is a function of the ratio of the largest to the smallest transition amplitudes (a1/a2).
Equation [3.151] is derived by noting that the signal amplitude beginning at –(a1/2) is increased by amount a2 at its peak. The ratio in dB by which the quick transition a3 fails to attain the same peak value as the slow transition + (a1/2) is called the dispersion penalty pd1:
)
The dispersion penalty may be expressed in terms of the ratio r of the amplitudes of the low- and high-frequency transitions:
)
|
where |
a1 equals the amplitude of the largest (slow-speed, or long run-length) transition, |
|
a2 equals the amplitude of the smallest transition (usually a quick transition like 010), |
|
|
r is the ratio a2/a1, and |
|
|
pd1 is the noise-tolerance penalty suffered at the receiver in exchange for having to deal with signal dispersion above and beyond low-frequency attenuation. |
Figure 3.46 charts the dispersion penalty pd1 as a function of r, with both quantities in units of dB. Due to the form of the dispersion-penalty equation, a received-amplitude ratio of 3dB causes a lot more than 3dB worth of degradation in the received amplitude. A received-amplitude ratio of 6 dB causes total receiver failure.
)
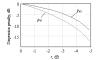Figure 3.46. The dispersion penalty is a function of the ratio r of the amplitudes of the highest and lowest-frequency signals on the line.
The dispersion penalty pd1 as defined here represents the worst-case received amplitude degradation above and beyond consideration of the attenuation of the lowest frequency (slow-speed, or long run-length) patterns present in the data waveform.
For noncoded random data, amplitude a1 is taken to be the peak-to-peak received amplitude at DC. For coded data waveforms having zero meaningful DC content (like Manchester coding, or 8B10B coding), amplitude a1 is taken to be the peak-to-peak received amplitude of the lowest possible frequency long-run-length sequence produced by the code.
The dispersion penalty could alternately be defined as the ratio in dB by which the quick transition amplitude a3 fails to attain the peak amplitude of a repeating fast transition sequence 101010.... The amplitude of this repeating fast-transition sequence is +(a2 / 2). In this case the dispersion penalty calculation is modified:
)
This dispersion penalty pd2 represents the worst-case received amplitude degradation above and beyond consideration of the attenuation of the highest frequency (quickest, or shortest run-length) patterns present in the data waveform.
Either penalty calculation can be used, as long as you remember the underlying basis of the definition. The difference between pd1 and pd2 equals precisely 20log(r).
An improvement in the dispersion penalty can be made in binary systems by a simple fixed-linear equalizer. Any monotonic, slowly changing equalization function that improves the ratio r, either by lowering the amplitude of the low-frequency transitions a1 or boosting the amplitude of the high-frequency transitions a2, will improve performance. The simple equalizer depicted in Figure 3.47 adjusts the transmitted signal magnitude during each bit interval to one of two values: a regular magnitude when repeating a bit, but double-magnitude when changing states. The combination of two magnitudes and two polarities results in a total of four possible transmit amplitudes that must be generated at the transmitter. By this scheme the received amplitude at the quick-transition locations is improved. This simple transmit-based equalization scheme can reliably boost the operating distance of a digital channel by 50% compared to the maximum reliable operating distance of an unequalized system. More elaborate equalization schemes can, if properly implemented, deliver even more impressive benefits.
)
Figure 3.47. A modest amount of fixed equalization improves the received eye pattern in a skin-effect limited or dielectric-effect limited
binary signaling channel.
The ratio r may be estimated, but not determined precisely, from a plot of the transfer function of the digital channel. For example, in Figure 3.43 the signal attenuation for a 0.5-m trace at a frequency of 1.25 GHz (half the data rate) amounts to roughly 5 dB, whereas the attenuation at 1/10th that rate (corresponding to a repeating pattern of 10 zeroes and 10 ones) amounts to roughly 1 dB, a difference of 4 dB. This difference is indicative, but not exactly equal to, the ratio a2/a1 in Figure 3.45. The reason such calculations are not exact is that the transfer function depicts the response to sine wave excitation at each particular frequency, whereas the desired variables a1 and a2 result from square wave excitation. Still, the transfer-function response ratio is often quite useful. My rule of thumb is that a system with less than 3 dB of difference in attenuation between the lowest relevant frequency and half the data rate will work reasonable well unequalized. Systems with a difference of more than 6 dB are marginal, and would benefit from fixed linear equalization. Systems with a difference of more than 12 dB generally require adaptive equalization, especially if you expect them to operate reliably at all channel lengths from zero to the maximum.