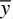Robust Design Example
The five-factor example used in Chapter 30 to illustrate a fractional factorial design can also be used here to demonstrate the Taguchi procedure for robust design. The five controllable inputs are shown in Table 31-4. The performance variable is film thickness, for which the target value is 1.0 mil.
Table 31-4. Controllable Inputs
|
Factor |
Low Setting |
High Setting |
|
X1 % Additive |
10 |
15 |
|
X2 Supplier |
1 |
2 |
|
X3 Production Rate (rolls/hr) |
100 |
120 |
|
X4 Temperature (°F) |
140 |
180 |
|
X5 Belt Speed (ft/min) |
25 |
50 |
Let's consider in addition two noise variables, relative humidity (low or high) denoted by Z1, and operating shift (1 or 2) denoted by Z2. The results from the 32-run design just presented in Table 31-3 are shown in Table 31-5.
Table 31-5. Experimental Results from Combined Inner and Outer Arrays
|
Z1 |
-1 |
-1 |
1 |
1 |
||||||||
|
X1 |
X2 |
X3 |
X4 |
X5 |
Z2 |
-1 |
1 |
-1 |
1 |
|
s |
ln(s) |
|
-1 |
-1 |
-1 |
-1 |
-1 |
0.92 |
0.86 |
0.83 |
0.84 |
0.862 |
0.0403 |
-3.21 |
|
|
-1 |
-1 |
-1 |
1 |
1 |
0.76 |
0.74 |
0.72 |
0.71 |
0.732 |
0.0222 |
-3.81 |
|
|
-1 |
1 |
1 |
-1 |
-1 |
0.96 |
0.89 |
0.95 |
0.94 |
0.935 |
0.0311 |
-3.47 |
|
|
-1 |
1 |
1 |
1 |
1 |
1.27 |
1.28 |
1.25 |
1.27 |
1.268 |
0.0126 |
-4.38 |
|
|
1 |
-1 |
1 |
-1 |
1 |
0.81 |
0.83 |
0.86 |
0.89 |
0.847 |
0.035 |
-3.35 |
|
|
1 |
-1 |
1 |
1 |
-1 |
0.92 |
0.88 |
0.95 |
0.94 |
0.923 |
0.031 |
-3.48 |
|
|
1 |
1 |
-1 |
-1 |
1 |
0.98 |
1.03 |
1.05 |
1 |
1.015 |
0.0311 |
-3.47 |
|
|
1 |
1 |
-1 |
1 |
-1 |
1.44 |
1.4 |
1.48 |
1.45 |
1.443 |
0.033 |
-3.41 |
Analyzing Average Performance
Taguchi advocates main effects plots for identifying controllable inputs that influence average performance. Main effects plots for average performance for this example are shown in Figure 31-1.
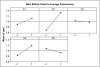
Figure 31-1 Main Effects Plots for Performance
These plots suggest that X2 (Supplier) has the largest effect on average performance (average film thickness), and that average performance is higher with Supplier 2 than with Supplier 1. Unfortunately, the target film thickness is almost exactly halfway between the average thickness obtained with material from Supplier 1 and the average thickness obtained with material from Supplier 2. In Minitab, clicking Stat > DOE Factorial > Analyze Factorial Design allows assessment of the statistical significance of this effect as well as other main effects and interaction effects, with the results shown in Figure 31-2 (after deleting nonsignificant combinations of interaction effects).
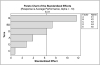
Figure 31-2 Pareto Summary of Effects for Average Performance
The main effect of the supplier is statistically significant at a significance level of 0.10, but so is the (Supplier)(Temperature) (i.e., X2X4) interaction effect, which is aliased with the (Production Rate)(Belt Speed) (X3X5) interaction effect. The main effect of Temperature (X4) is marginally significant at this significance level. This analysis demonstrates the danger of relying on only main effects to identify influential inputs. All other effects, each of which is aliased with three other effects, are indicated to have no significant influences on average performance.
An interaction plot involving the supplier and temperature (X2 and X4), shown in Figure 31-3, reveals that the preferred conditions for those two controllable inputs for achieving the target thickness are with material from Supplier 2 at temperature 140 °F, conditions that are not apparent from the main effects plots alone.

Figure 31-3 (Supplier)(Temperature) (X2)(X4) Interaction Plot
Analyzing Variation in Performance
A similar analysis performed on ln(s) produces the results shown in Figure 31-4.

Figure 31-4 Main Effects Plots for Loge Standard Deviation of Performance
These main effects plots suggest that all (or none) of the controllable inputs may influence variation in performance (variation in film thickness). The statistical significance (at the 0.10 level) of the main effect of each of the five controllable inputs is shown in Figure 31-5. The interaction effects that are not aliased with main effects are found to be nonsignificant.
Figure 31-5 Pareto Summary of Effects for Loge Standard Deviation of Performance
The summary indicates that only three of the controllable inputs, Temperature (X4), Belt Speed (X5), and % Additive (X1), significantly influence the variation in performance.
From these results, it appears that average film thickness = 1.0 mil could be achieved with low variation in performance with the following settings:
|
X1 |
% Additive |
10 |
|
X2 |
Supplier |
2 |
|
X3 |
Production Rate (rolls/hr) |
120 (as high as possible because it has no apparent effect on average performance or variation in performance) |
|
X4 |
Temperature (°F) |
140 |
|
X5 |
Belt Speed (ft/min) |
50 |
However, there is clearly a conflict concerning the best setting for temperature (x4). To achieve an average film thickness close to target, the best temperature is 140°F, but to achieve minimum variation in film thickness, the temperature should be 180°F. An optimal compromise solution can be found using Multiple Response optimization, which is discussed in Chapter 33.+