- Calculating Loan Payments
- Calculating Principal Payments
- Working with Future Value
- Using the Present Value Function
- Calculating Interest Rate
Calculating Principal Payments
When you make a payment on a loan, each payment is divided into two parts:
Part of the payment is for that month’s interest charge.
The remainder of the payment goes toward paying down the principal.
Each month you pay down the loan balance, or principal, by some amount. This means that the next month the interest charge will be less because the charge is calculated as the interest rate multiplied by the balance. The total payment amount is fixed, which means that each succeeding month less of your payment goes toward interest and more toward the principal. To calculate the amount that goes toward principal for a specific payment, use the PPMT function.
To see an example of this, please refer to Figure 3.2. This worksheet presents an amortization table for a $10,000 loan at 5% for 12 months. The three columns of data are
Principal—The amount of each payment that goes toward the loan balance. This is calculated with the PPMT function. You can see that this amount increases for subsequent payments.
Interest—The amount of each payment that goes toward interest. This is calculated with the IPMT function (covered in the next section). You can see that this amount decreases for subsequent payments.
Total—The total monthly payment, the sum of principal and interest. This amount stays constant for the entire term of the loan.
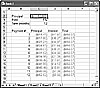
Figure 3.2 This amortization table shows how the principal payment increases while the interest payment decreases over the life of a loan.
The PPMT function uses the following syntax; you’ll note that most of the arguments are the same as for the PMT function:
The first four arguments are required. They are
rate is the interest rate for the loan.
per is the period for which you want the principal payment. This argument must be in the range 1 to nper.
nper is the term of the loan expressed as the number of payment periods.
prin is the principal, the amount you are borrowing.
As explained earlier for the PMT function, both rate and nper must use the same time unit (usually months). The last two arguments are optional (as indicated by the brackets in the formula):
fv is the future value of the loan, or the amount still owed when you have completed payments. Because loans are almost always paid off in full, you will use 0 for this argument or omit it, in which case Excel assumes 0.
type indicates when payments are made. Use a value of 1 if payments are made at the start of each period. Use a value of 0, or omit the argument, if the payment is made at the end of each period.
In most situations you omit both of these optional arguments.
To try out the PPMT function, you can add to the worksheet you created earlier for the PMT function (refer to Figure 3.1). Then follow these steps:
Put the labels For payment #, Principal, and Interest in cells B7 through B9, in order.
Put the following formula in cell C8: =PPMT(C3/12,C7,C4*12,C2).
Put the following formula in cell C9: =C5-C8.
Format cells C8 and C9 as currency with two decimal places.
A sample calculation is shown in Figure 3.3. You can see that for the specified loan, the first payment consists of $232.29 going toward principal and $73.33 going toward interest. Change the payment number to 60—the last payment for the loan— and you’ll see the amounts change to $304.22 and $1.39 respectively.
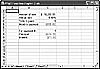
Figure 3.3 Using the PPMT function to calculate the principal component of loan payments.