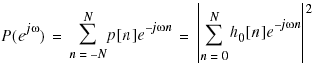- 1 Two-Channel Perfect Reconstruction Filter Banks
- 2 Orthogonal Filter Banks
- 3 General Tree-Structure Filter Banks and Wavelet Packets
6.2 Orthogonal Filter Banks
The relationship defined by Eq. (6.9) ensures that the analysis and synthesis filters are orthogonal in the sense of
(6.29)
However, the condition (6.29) alone does not ensure that the resulting filter banks {hi[n]} or {γi[n]} form orthogonal filter banks and that the resulting wavelets are orthogonal wavelets, such as in the case of the spline wavelets in Example 6.1 a and b. In these cases, there are two sets of scaling functions and mother wavelets. Neither the analysis bank nor the synthesis bank satisfies the power complementarity condition (5.63), i.e.,
(6.30)
and
(6.31)
Figure 6-8 plots Eqs.(6.30) and (6.31) for the quadratic spline wavelets in Example 6.1 a. Although the filters in (6.29) meet the condition of perfect reconstruction, the transformation formed by the set of filters Hn(ω) or Gn(ω) is not energy conserving.
Figure 6-8 In the biorthogonal case, neither the analysis filter bank Hn(ω) nor the synthesis filter bank Gn(ω) satisfy the power complementarity condition. The bases of biorthogonal wavelets do not reproduce the signal energy exactly.
For the filter banks in Example 6.1 a and b the relation corresponding to (5.56) has a form
(6.32)
we name the resulting filter banks the biorthogonal filter banks.
In addition to Eq. (6.29), if the filters of the PR filter banks also satisfy the following relationship
(6.33)
then the resulting filter banks are orthogonal filter banks. Obviously, it is a special case of the biorthogonal filter banks. For the orthogonal filter banks, the synthesis and the analysis filters are related by time reversal. The reader can verify that the filter banks for the Daubechies wavelets in Eqs. (6.26) and (6.27) satisfy the condition (6.33).
For orthogonal filter banks, once the product filter P0(z) is selected, we only need to define H0(z). With H0(z), as we will see shortly, we can easily find all the other filters. Many applications demonstrate that the lack of orthogonality complicates quantization and bit allocation between bands, eliminating the principle of conservation of energy. The bases of biorthogonal wavelets do not reproduce the signal energy exactly. Reconstructing a signal from these coefficients may amplify any error introduced in the coefficients. Hence, orthogonal filter banks are often the first choice when we factor the product filter P0(z). The remaining question is: What constraints does P0(z) have to meet for orthogonal filter banks?
To achieve Eq. (6.33), we can let
(6.34)
which implies that h1[n] is the alternating flip of h0[n], i.e.,
(6.35)
From Eqs. (6.9) and (6.34), we can readily compute G0(z) and G1(z). For example,
(6.36)
Therefore, γ0[n] is the flip of h0[n], i.e.,
(6.37)
Substituting Eq. (6.36) into Eq. (6.16), we have
(6.38)
If we define
(6.39)
then
(6.40)
Moreover,
(6.41)
which implies that P(z) is non-negative. P0(z) is the time-shifted non-negative function P(z). It can be shown that the maximally flat filter defined in Eq. (6.18) ensures that this requirement is met. However, special care must be taken when P0(z) has other forms, such as an equiripple halfband filter [47]. Table 6-1 compares different types of filters. Note that the filter banks cannot be orthogonal and linear phase simultaneously.
Table 6-1 Digital Filters for PR Filter Banks
|
Filter Type |
Location of Zeros |
Comments |
|
Real |
Complex conjugate symmetrical |
|
|
Linear Phase |
Each filter must contain both zi and its reciprocal 1/zi. (The pair of reciprocals must be in the same filter.) |
Desirable for image processing |
|
Minimum Phase |
All zeros have to be on or inside of the unit circle. |
Minimum phase lag |
|
Orthogonal |
Each filter cannot have zi and its reciprocal 1/zi simultaneously. zi and its reciprocal 1/zi have to be in separate filters. This condition is contradictory to that required for linear phase filters. |
Analysis and synthesis have the same performance Even length (N odd) Convenient for bit allocation and quantization error control Not linear phase |
The discussion in this section has been focused on the two-channel perfect reconstruction filter banks. The relationship of the Fourier transform and the scaling function to the frequency response of the FIR filter is given by the infinite products (5.47). From these connections, we reason that since H0(z) or G0(z) is lowpass and, if it has a high order zero at z = -1 (i.e., ω = p), the Fourier transform of the analysis/synthesis scaling function φ(t) should drop off rapidly and, therefore, φ(t) should be smooth. It turns out that this is indeed true. This is related to the fact that the differentiability of a function is tied to how fast the magnitude of its Fourier transform drops off as the frequency goes to infinity.
It can be shown [6] that the number of zeros at z = -1 of the lowpass filter H0(z) or G0(z) determines the number of zero moments of the wavelets. Table 6-2 lists the discrete and continuous moments of the second (db2, see Example 6.1) and third order (db3) Daubechies scaling function and wavelets. While the continuous moments are defined in (5.79) and (5.80), the discrete moments are defined as
(6.42)
and
(6.43)
The Daubechies filter coefficients ensure the maximum number of zero moments of the wavelets (or maximum vanishing moments), which is weakly related to the number of oscillations. Researchers have also recognized that in some applications, the zero moments of the scaling function are also useful.4 However, the filters yielding a combination of zero wavelet and zero scaling function moments cannot be directly generated by the filter P0(z) or P(z) that were introduced earlier. The design of these kinds of filters need to employ other techniques that are beyond the scope of this book. The resulting wavelets are traditionally named coiflets. The reader can find related materials in [13], [270], [247], [288], and [400].
Table 6-2 Moments of Daubechies Scaling and Wavelet Functions [6]
|
k |
Scaling Functions |
Wavelets |
||||||
|
μ0[k] |
m0[k] |
μ1[k] |
m1[k] |
|||||
|
db2 |
db3 |
db2 |
db3 |
db2 |
db3 |
db2 |
db3 |
|
|
0 |
1.41421 |
1.41421 |
1.00000 |
1.00000 |
0 |
0 |
0 |
0 |
|
1 |
0.89657 |
1.15597 |
0.63439 |
0.81740 |
0 |
0 |
0 |
0 |
|
2 |
0.56840 |
0.94489 |
0.40192 |
0.66814 |
1.22474 |
0 |
0.21650 |
0 |
|
3 |
-0.8643 |
-0.2243 |
0.13109 |
0.44546 |
6.57201 |
3.35410 |
0.78677 |
0.29646 |
|
4 |
-6.0593 |
-2.6274 |
-0.3021 |
0.11722 |
25.9598 |
40.6796 |
2.01434 |
2.28246 |
|
5 |
-23.437 |
5.30559 |
-1.0658 |
-0.0466 |
90.8156 |
329.323 |
4.44427 |
11.4461 |
The theory of perfect reconstruction filter banks was developed a long time before wavelet analysis became popular, but the original filter banks had no vanishing moments and thus did not always generate finite energy wavelets. "The connection between the number of vanishing moments of a filter and the corresponding wavelet having finite energy is not immediately apparent. But having a conjugate mirror filter h[n] such that its Fourier transform H(ω) vanishes at ω = þ (z = -1) is a necessary condition so that the cascade of such filters defines a finite energy scaling function and hence a finite energy wavelet. In addition, the number of vanishing moments of a wavelet is equal to the number of zeros of the Fourier transform of its filter at ω = þ; saying that a wavelet has one vanishing moment is equivalent to saying that H(p) = 0. More generally, if a wavelet has k vanishing moments, then H(ω) and its first k - 1 derivatives vanish at ω = 0" [22].
Unlike the Fourier transform in which there is only one set of basis functions, for the wavelet transform one can choose from an infinite number of mother wavelets. The success of the application of wavelet analysis largely hinges on the selection of the mother wavelet. In most applications, such as denoising, the ideal wavelet is one that will encode a signal using the greatest possible number of zero coefficients, or the majority of coefficients closest to zero. Unfortunately, such requirements cannot be described mathematically in most cases. The most effective procedure for selecting a proper mother wavelet may be though trial and error. With the help of computer software, such as the Signal Processing Toolset provided by National Instruments, engineers and scientists now can immediately see the effect on their data samples of selecting between different product filters P0(z) and factorization schemes.